математика комплексное. Если вторая производная дважды дифференцируемой функции yf(x) отрицательна(f(x)0), то кривая вогнутая на (ab)
 Скачать 78.71 Kb. Скачать 78.71 Kb.
|
|
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график, но поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Пусть функция 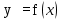 является дифференцируемой, является дифференцируемой, 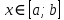 , её производная , её производная 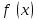 — функция, которая также дифференцируема. Тогда можно найти производную — функция, которая также дифференцируема. Тогда можно найти производную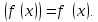 Это производная второго порядка, или вторая производная функции Это производная второго порядка, или вторая производная функции 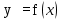 . .Например, найти производную 2-го порядка функции y=x3 -4x2+5x-6 означает найти производную этой функции y`=3x2-8x+5 и полученную функцию продифференцировать:y``=6x-8. Кривая y=f(x) называется выпуклой на интервале, (a;b) если все её точки, кроме точки касания, лежат ниже произвольной её касательной на этом интервале (на рис. 86 — 1). Кривая y=f(x) называется вогнутой на интервале (a;b) если все её точки, кроме точки касания, лежат выше произвольной её касательной на этом интервале (на рис. 86 — 2). 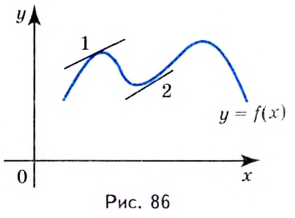 Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой. Интервалы выпуклости и вогнутости находят при помощи такой теоремы. Теорема. Если вторая производная дважды дифференцируемой функции y=f(x) отрицательна(f``(x)<0) на интервале(a;b), то кривая y=f(x) выпуклая на данном интервале; если вторая производная функции y=f(x) положительная(f``(x)>0), то кривая вогнутая на (a;b). Из теоремы следует, что точками перегиба кривой y= f(x) могут быть только точки, в которых вторая производная f``(x) равна нулю или не существует. Такие точки называют критическими точками второго рода. Установим достаточное условие существования точки перегиба. Теорема. Пусть Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой: найти область определения функции; найти критические точки второго рода; определить знак второй производной на образованных интервалах. Если f``(x)<0, то кривая выпуклая; если f``(x)>0 — кривая вогнутая; если производная f``(x) меняет знак при переходе через точку |
