урок 9 статистика (1). Этапы построения статистических группировок

• Название: Этапы построения статистических группировок
• Дата: 29.09.2022
• Размер: 41.22 Kb.
• Имя файла: урок 9 статистика (1).docx
• Тип: Документы; #706066

Этапы построения статистических группировок

1. 
   Определение группировочного признака.
   
2. 
   Определение размаха вариации.
   
3. 
   Определение числа групп.
   
4. 
   Расчет ширины интервала группировки.
   
5. 
   Определение признаков, которые в комбинации друг с другом будут характери­зовать каждую выделенную группу.
   

При небольшом объеме совокупности (n<50) не следует образовывать большого количества групп, так как группы будут включать недостаточное число единиц объекта. Показатели, рассчитанные для таких групп, не будут представительными и не позволят получить адекватную характеристику исследуемого явления.

Часто группировка по количественному признаку имеет задачу отразить распреде­ление единиц совокупности по этому признаку. В этом случае количество групп зависит, в первую очередь, от степени колеблемости группировочного признака: чем больше его колеблемость, тем больше можно образовать групп.

При определении числа групп необходимо принять во внимание размах вариации признака (R), который позволяет оце­нить вариацию признака между крайними значениями признака –  максимальным (Х_max) и минимальным (X_min) и определяется по формуле 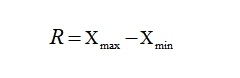5.1):                                                                                                                                                                                                                                                                                                                                          (5.1)

Чем больше размах вариации признака, положенного в основание группировки, тем, как правило, может быть образовано большее число групп. При этом может возникнуть проблема получения пустых групп, т.е. групп, не содержащих ни одной единицы наблюдения.

Если группировка строится по атрибутивному признаку, то групп, как правило, будет столько, сколько имеется градаций, видов состояний у этого признака. Если группировка строится по количественному признаку, то необходимо обратить внимание на число единиц совокупности, степень вариации группировочного признака и цели исследования. Оптимальное число групп может быть определено по формуле Стерджесса.

Определение числа групп можно осуществить несколькими способами. Формально-математический способ предполагает использование формулы Стерджесса (формула 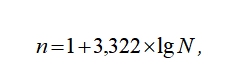5.2):                                                                                                                                                                                                                                                                                                 (5.2)

гдеn – число групп; N –  число единиц совокупности.

Согласно этой формуле выбор числа групп зависит только от объема изучаемой совокупности.

Применение данной формулы дает хорошие результаты в том случае, если сово­купность состоит из большого числа единиц наблюдения (n>50).

Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения (σ). Если величина интервала равна 0,5σ, то совокуп­ность разбивается на 12 групп, а когда величина интервала равна 2/3σ и σ, то совокуп­ность делится, собственно, на 9 и 6 групп. Однако при определении групп данными методами существует большая вероятность получения «пустых» или малочисленных групп, характеристики изучаемого явления на основе которых будут недостаточно типичными для выделенной группы и изучаемой совокупности в целом.

Когда определено число групп, то следует определить интервалы группировки.

Интервал – это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет верхнюю и нижнюю границы или одну из них. Нижней границей интервала называется наименьшее значение признака в интервале. Верхней границей интервала называется наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами интервала.

Интервалы группировки бывают: равные и неравные; открытые и закрытые.

Ширина равного интервала определяется по (формуле 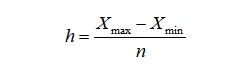5.3):

(5.3)

Если максимальные или минимальные значения сильно отличаются от смежных с ними значений вариантов в упорядоченном ряду значений группировочного признака, то для определения величины интервала следует использовать не максимальное или минимальное значения, а значения, несколько превышающие минимум, и несколько меньше, чем максимум.

Полученную по формуле (5.3) величину округляют, и она будет являться шириной интервала.

Существуют следующие правила определения ширины интервала.

Если величина интервала, рассчитанная по формуле (5.3) представляет собой величину, которая имеет один знак до запятой (например, 0,67; 1,487; 3,82), то в этом случае полученные значения целесообразно округлить до десятых и их использовать в качестве ширины интервала. В приведенном выше примере это будут соответственно значения: 0,7; 1,5; 3,8.

Если рассчитанная величина интервала имеет две значащие цифры до запятой и несколько после запятой (например, 14,876), то это значение необходимо округлит до целого числа (15).

В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, то эту величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 652 следует округлить до 650 или до 700.

Если размах вариации признака в совокупности велик и значения признака варьируют неравномерно, то надо использовать группировку с неравными интервалами.

Неравные интервалы могут быть получены в процессе объединения пустых, не содержащих ни одной единицы совокупности, равных интервалов. Это происходит в том случае, если после построения равных интервалов по изучаемому признаку образуются группы, содержащие мало или не содержащие вообще ни одной единицы, т.е. группы, не отражающие определенных типов изучаемого явления по признаку. В этом случае возникает необхо­димость в увеличении интервалов группировки.

Также неравные интервалы могут быть прогрессивно-возрастающие или прогрес­сивно-убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической и геометрической прогрессии, определяется следующим образом: h_i+1=h_i+а,

а в геометрической прогрессии: h_i +1= h_i ×q, где:

а – константа: для прогрессивно-возрастающих интервалов имеет знак «+», а при прогрессивно-убывающих – знак «-».

q — константа: для прогрессивно-возрастающих – больше «1»; для прогрессивно-убывающих ‑ меньше «1».

Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница не существенна.

Например, при построении группировки строительных компаний города по показателю численности работающих, который варьирует от 500 человек до 3500 человек, нецелесообразно рассматривать равные интервалы, т. к. учитываются как малые, так и крупнейшие строительные фирмы города. Поэтому следует образовывать неравные интервалы: 500–1000, 1000–2000, 2000–3500, т.е. величина каждого последующего интервала больше предыдущего на 500 человек и увеличивается в арифметической прогрессии. Выбор исследователя в построении равных или неравных интервалов зависит от степени заполнения каждой выделенной группы, т.е. от числа единиц в них. Если величина интервала существенна и содержит большое число единиц совокупности, то эти интервалы необходимо дробить, а в противном случае – объединять.

Интервалы статистической группировки

Интервалы группировок могут быть закрытыми и открытыми.

Закрытые интервалы – это интервалы, у которых есть и верхняя и нижняя границы.

Открытые интервалы – это интервалы, у которых указана только одна граница: как правило, верхняя – у первого интервала и нижняя – у последнего.

Например, группы страховых компаний по числу работающих в них сотрудников (чел.): до 50, 50–100, 100–150, 150 и более. Применение открытых интервалов целесообразно в тех случаях, когда в совокупно­сти встречается незначительное число единиц наблюдения с очень малыми или очень большими значениями вариантов, которые резко, в несколько раз, отличаются от всех остальных значений изучаемого признака.

Если основанием группировки служит непрерывный признак (например, группы строительных фирм по объему строительно-монтажных работ, выполненных собственными силами (тыс. руб.): 1200–1400, 1400–1600, 1600–1800, 1800–2000), то одно и то же значение признака выступает и верхней и нижней границами двух смежных интервалов. В данном случае объем работ 1400 тыс. руб. составляет верхнюю границу первого интервала и нижнюю границу второго, 1600 тыс. руб. ‑ соответственно второго и третьего и т.д., т.е. верхняя граница i-го интервала равна нижней границе (i+1)-го интервала.

При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы наблюдения, значения признака у которых совпадают с границами интервалов.

Например, во вторую или третью группу должна войти строительная фирма с объемом строительно-монтажных работ 1600 тыс. рублей? Если верхняя граница формируется по принципу «исключительно», то фирма должна быть отнесена к третьей группе, в противном случае – ко второй. Для того, чтобы правильно отнести к той или иной группе единицу совокупности, значение признака которой совпадает с границами интервалов, можно ориентироваться на открытые интервалы (по нашему примеру группы строительных фирм по объему строительно-монтажных работ преобразуются в следующие: до 1400, 1400–1600, 1600–1800, 1800 и более). В данном случае, вопрос отнесения отдельных единиц совокупности, значения которых являются граничными, к той или иной группе решается на основе анализа последнего открытого интервала. Возможны два случая обозначения последнего открытого интервала: 1) 1800 тыс. руб. и более; 2) более 1800 тыс. руб. В первом случае, строительные фирмы с объемом строительно-монтажных работ 1600 тыс. руб. попадут в третью группу; во втором случае – во вторую группу.

Если в основании группировки лежит дискретный признак, то нижняя граница 1-го интервала равна верхней границе i-1-го интервала, увеличенной на 1.

Например, группы строительных фирм по числу занятого персонала (чел.) будут иметь вид: 100–150, 151–200, 201–300.

Строя такую группировку, следует дифференцированно устанавливать границы интервалов для разных отраслей народного хозяйства. Это достигается путем использования группировок со специализированными интервалами.

Специализированные интервалы – применяются дли выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях.

При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно-возрастающими, ни прогрессивно-убывающими. Такие интервалы называются произвольными и, как правило, используются при группировке предприятий, например, по уровню рентабельности.