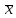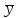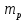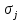Практическое задание Теория отраслевых рынков. Факторы, определяющие структуру рынка Задание
 Скачать 43.02 Kb. Скачать 43.02 Kb.
|
|
Факторы, определяющие структуру рынка 1.Задание Предприятие в процессе своей деятельности должно выбирать такую стратегию, которая позволит снизить степень риска. Существует ряд приемов снижения риска: предвидение, создание гарантийных или резервных фондов, которые заранее подготавливают их покрытие, страхование, получение гарантий, что уменьшает долю возможных убытков и новый прием – диверсификация производства. Диверсификация производства – это одновременное развитие многих, не связанных или слабосвязанных друг с другом видов деятельности, номенклатуры продукции (работ, услуг), ассортимента производимых изделий в масштабе государства, отрасли, региона, предприятия. В результате диверсификации производства предприятия превращаются в сложные многоцелевые комплексы, включающие производства, зачастую выпускающие продукцию и оказывающие услуги совершенно различного назначения и характера. В основе диверсификации лежат факторы экономической выгоды комбинированного производства, которое приобретает большую устойчивость к колебаниям рыночной конъюнктуры, расширяет возможности маневрирования номенклатурой продукции, приспосабливается к изменяющемуся спросу. При падении спроса на одни виды продукции (услуги) предприятие расширяет производство других видов, обеспечивая при этом необходимый уровень рентабельности. Расчет ожидаемых значений эффективностей диверсификации производства состоит в следующем. Пусть xi, j=1 … n – доля общего вложения, приходящаяся на j-й вид деятельности, так, что Σxi=1, тогда эффективность Rp равна 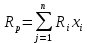 Согласно правилам теории вероятностей, ожидаемый эффект от видов деятельности предприятия равен 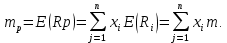 Отклонение от ожидаемого значения 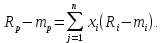 Математическое ожидание квадрата этого отклонения есть дисперсия эффекта видов деятельности 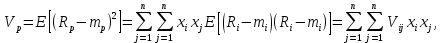 где величины Vijj = 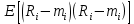 являются ковариациями величин Ri,Rj. являются ковариациями величин Ri,Rj.Очевидно, что Vij является дисперсией Rj. Так как случайные эффекты от различных видов деятельности независимы, точнее некоррелированы (Vij=0,i≠j), тогда 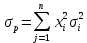 а среднеквадратическое отклонение равно 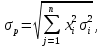 Именно эта величина характеризует неопределенность, риск, связанный с выбором того или иного продукта (вида деятельности) и вложением в него денежных средств, который принесет ожидаемый эффект. Допустим, предприятие вложило во все виды деятельности денежные средства равными долями. Тогда xi=1/n, и средний эффект равен 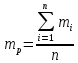 (П4.1) (П4.1)причем риск равен 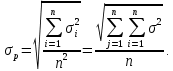 Тогда пусть σ = max 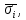 то то 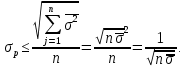 (П4.2) (П4.2)Следовательно, при росте числа nвидов продукции, риск ограничен и стремится к 0, при n→∞. Этот результат в теории финансового риска называется эффектом диверсификации продукции. Отсюда вытекает главное практическое правило: для повышения надежности эффекта от вклада в рискованные виды продукции целесообразно делать вложения не в один вид продукции, а в содержащие как можно больше разнообразных видов, эффект от которых случаен, но случайные отклонения независимы. Так и перед анализируемым предприятием стоят два пути распределения прибыли. Во-первых, сконцентрированность собственного производства на видах продукции, дающих максимальный эффект, но при этом и финансовый риск будет максимален. Во-вторых, рассредоточенность производства по всем видам продукции, снижающим экономический эффект, но и уменьшающим финансовый риск. Группировка основных видов продукции с помощью экономико-математической модели и оценка степени финансового риска помогут сделать правильный выбор. Важнейшим этапом анализа большого числа многомерных объектов является задача классификации, которую можно рассматривать как поиск решения, позволяющего наилучшим образом разделить множество объектов на более мелкие однородные группы. Один из возможных путей классификации – использование кластерного анализа. Он позволяет классифицировать объекты по модулю и фазе вектора в n-мерном пространстве признаков. На рисунке П4.1 приведен пример классификации в двухмерном пространстве. Множество изделий состоит из четырех пересекающихся подмножеств S1,S2,S3,S4. Подмножества S1 и S2 различаются соотношением параметров X и Y. Но модули их векторов приблизительно равны, поэтому при классификации по изложенному методу подмножества S1 и S2 войдут в один класс с важной степенью близости. Аналогично другой класс, с более высоким обобщенным показателем образует подмножества S3 и S4, создается возможность компенсации низкого уровня одного параметра за счет другого. Например, YS2 за счет XS2. Другая классификация по модулю и фазе методами кластерного анализа требуют меры близости объектов определять не только по модулю, но и по фазам, т.е. перехода от одно- к многомерной классификации объектов. Данный метод кластерного анализа осуществляется с помощью построения дендрограмм. 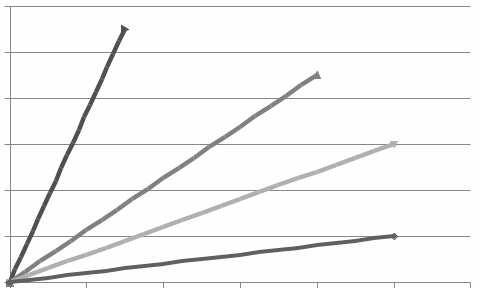 Рис. П4.1. Классификация объектов по модулю и фазе векторов Сущность метода построения дендрограмм заключается в следующем. Пусть имеется класс объектов Ai, i=1,2 … n, характеризуемых набором признаков 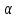 ip = 1,2 … k. Основная идея – это построение иерархической системы, объединяющей группы сходных объектов. Известно, что коэффициенту корреляции можно придать геометрический смысл, интерпретируя его как косинус угла между двумя векторами в n-мерном евклидовом пространстве. Тогда arcos коэффициента корреляции можно рассматривать как меру расстояния между двумя векторами, а следовательно, как меру сходства между объектами. ip = 1,2 … k. Основная идея – это построение иерархической системы, объединяющей группы сходных объектов. Известно, что коэффициенту корреляции можно придать геометрический смысл, интерпретируя его как косинус угла между двумя векторами в n-мерном евклидовом пространстве. Тогда arcos коэффициента корреляции можно рассматривать как меру расстояния между двумя векторами, а следовательно, как меру сходства между объектами.Коэффициент корреляции вычисляется по формуле 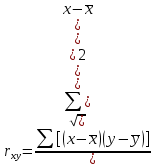 где х,у – рентабельность продукции (продаж); n – количество лет. Основой для применения любого метода группировки объектов во взаимно связанные группы служит симметрическая матрица S, элементы которой Sijявляются расстояниями между объектами Ai,Aj/Sij=arcos rai,aj. Построение дендрограмм представляет собой последовательную процедуру объединения ближайших элементов или групп в новую группу. На первом шаге объединяются два объекта Ai,Aj, которым соответствует минимальный элемент (расстояние) матрицы S. Значение близости двух наиболее сходных объектов запоминается и рассматривается в дальнейшем кА величина, характеризующая иерархический уровень первой стадии группировки. На каждом последующем этапе необходимо вновь выбрать два наиболее близких объекта, объединить их и значение иерархического уровня образованной группы запомнить. Очевидно, что при исходном числе элементов, равном n, вся процедура заканчивается на (n-1)-м шаге. Заметим, что при объединении двух объектов, содержащих несколько элементов Ai, за меру группового сходства можно принять среднеарифметическое расстояние между элементами объединенных групп. Необходимо произвести расчеты, исходя из данных по рентабельности продукции и рентабельности продаж, за пять лет по семи видам продукции. Группировка основных фондов продукции выглядит так. Сначала необходимо найти коэффициент корреляции, сравнивая первые два вида продукции, затем рентабельности первого и третьего видов продукции. Сравнив рентабельность первого вида продукции с последующими, переходим к сравнению второго вида продукции с остальными видами. Пример расчета Используя исходные данные о рентабельности продаж необходимо провести группировку товаров и выбрать стратегию, максимизирующую эффективность деятельности и снижающую финансовый риск. Таблица П4.1 Показатели рентабельности продаж
Расчет группировки товара А(x1) и товара Б(x2) приведен в табл. П4.2. Таблица П4.2 Корреляционная матрица группировки
Подставив данные табл. П4.2 в формулу (П4.3), найдем коэффициент корреляции данных видов продукции 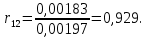 Расчет группировки последующих видов аналогичен. Находим arcos 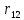 = arcos 0,929 = 0,379. = arcos 0,929 = 0,379.Также находится arcos остальных коэффициентов корреляции. После расчетов всех коэффициентов данные заносятся в табл. П4.3. Таблица П.4.3 Корреляционная матрица группировки видов продукции
Имея необходимы данные, можно приступить к группировке основных видов продукции. Данные табл. П4.3 группируются по признаку наименьшего показателя. Группировка начинается с двух видов продукции и заканчивается всеми сгруппированными видами продукции. 1) <2,3> ; h1= 0,0872; 2) <2,3,4>; h2= (S23+S24+S34)/3=0,7317/3=0,2439; 6) <1,2,3,4>;h3= ΣS/6=0,305. Теперь, когда виды продукции сгруппированы, можно приступать к построению дендрограммы группировки основных видов продукции, которая представлена на рис. П4.2.
Рис. П4.2. Дендрограмма группировки основных видов продукции Экономико-математическая группировка основных видов продукции показала существование трех вариантов диверсификации продукции на анализируемом предприятии. Уровни диверсификации по вариантам продукции различны, начиная от минимального (для <2,3>;<2,3,4>;<1,2,3,4>. Первой строится матрица группировки товара Б и товара В (табл. П4.4). Таблица П4.4 Матрица группировки <2,3>
В таблице П4.4 mj = Rj – средняя рентабельность за пять лет, следовательно: 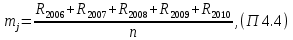 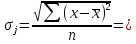 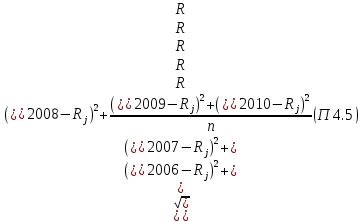 где mp – эффект от диверсификации; σj – риск. Связанный с диверсификацией. По формуле П4.4 рассчитываем среднюю рентабельность второго и третьего вида продукции: m2 = (28,30+29,0+30,0+31,5+31,7)/5=30,1; m3 = (29,2+31,0+31,0+32,3+32,7)/5=31,24. По формуле П4.1 рассчитывается эффект от диверсификации: 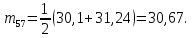 По формуле П4.4 рассчитывается риск по второму и третьему виду продукции: 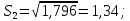 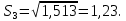 Риск, связанный с диверсификацией второго и третьего видов продукции рассчитывается по формуле П4.2: 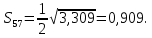 Расчеты остальных групп матриц идентичны. Используя результаты расчетов, необходимо составить обобщенную табл. П4.5, с помощью которой можно сделать вывод об эффекте от диверсификации и финансовом риске. Таблица П4.5 Оценка эффективности финансового риска от диверсификации продукции
Следовательно, наилучшей группировкой видов продукции по показателю максимальной эффективности продукции является вариант диверсификации <1,2,3,4> т.е. объединение всех групп продукции. При этом сочетании эффект равен 31,445 единицы, а риск – 0,616 единицы. По критерию наименьшего финансового риска предпочтение следует отдать варианту диверсификации <2,3,4>. В этом случае величина финансового риска равна 0,608, а эффект от диверсификации – 28,69 единицы. Таким образом, возникает проблема выбора вариантов диверсификации по двум критериям. Чтобы решить её, необходимо сопоставить выигрыш от повышения эффекта в случае предпочтения варианта <2,3,4>, с выигрышем от снижения риска в случае выбора варианта <1,2,3,4>. Предприятию необходимо сосредоточиться на производстве всех видов продукции, но исключая иногда товар А(1). Рисунок П4.3 показывает соотношение, в котором должны производиться два варианта группировки видов продукции на основе показателей рентабельности продаж. Другими словами, из 10 раз 1 раз необходимо производить 2,3,4-й вид продукции и 9 раз 1,2,3-й и 4-й вид продукции (1:9). Применение предложенной смешанной стратегии позволит предприятию добиться оптимального результата с учетом максимальной эффективности продукции и минимального финансового риска.
Рис. П4.3. Соотношение производства доминирующих вариантов группировок продукции на основе показателей рентабельности продаж Исходные данные для расчета Вариант 1 Показатели рентабельности продаж
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||