Факультет математики и компьютерных наук Кафедра вычислительной математики и информатики индивидуальное задание по учебной практике
 Скачать 41.24 Kb. Скачать 41.24 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «КубГУ») Факультет математики и компьютерных наук Кафедра вычислительной математики и информатики ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ ПО УЧЕБНОЙ ПРАКТИКЕ Работу выполнил И.А. Сафонов (подпись) Направление подготовки 02.03.01 курс 2 Научный руководитель Канд. тех. наук, доцентЕ.Р. Алексеев (подпись, дата) Нормоконтролер преподавательЕ.Р. Алексеев (подпись, дата) Краснодар 2022 СОДЕРЖАНИЕ 1Условие 4 2Программа 5 3Результат работы 11 11 Условие Задание № 1. Обработка результатов эксперимента. Интерполяция функций. В результате эксперимента была определена некоторая табличная зависимость. Построить интерполяционную функцию. Вычислить ожидаемое значение функции в указанных точках. Построить график, на котором изобразить экспериментальные точки, график интерполяционной зависимости, ожидаемое значение в указанных точках. Реализовать следующие методы интерполяции: интерполяционный полином Лагранжа; интерполяционный полином Ньютона; канонический полином; функция линейной интерполяции. Задачу решить двумя способами. Используя математический пакет (Scilab или любой другой). Написав программу на языке С(С++).  Программа #include for(i=0;i { *pval_arr++ = (float *)malloc(sizeof(float)*2); } pval_arr-=quan_dot; entry_the_value(pval_arr,quan_dot); fd = open(path,O_WRONLY|O_TRUNC); char buf[BUF_SIZE]; for(i=0;i { len = sprintf(buf,"%f",pval_arr[i][0]); write(fd,buf,len); write(fd," ",1); len = sprintf(buf,"%f",pval_arr[i][1]); write(fd,buf,len); write(fd,"\n",1); } printf("\nInput quan of test dots :"); scanf("%d",&quan_tdot); float * ptdot_arr = (float *)malloc(sizeof(float)*quan_tdot); for(i=0;i { printf("\nInput test dot[%d] = ",i);scanf("%f",ptdot_arr++); } ptdot_arr-=quan_tdot; float res_cur=0; int flag; for(i=0;i { res_cur=0; for(j=0;j { inter_val=1; for(k=0;k { if(k==j) continue; if(*ptdot_arr== (*pval_arr)[0]) { flag = 1; break; } inter_val*=(*ptdot_arr-pval_arr[k][0])/(pval_arr[j][0]- pval_arr[k][0]); } res_cur+= flag ? pval_arr[j][1] : pval_arr[j][1]*inter_val; flag =0; } len = sprintf(buf,"%f",*ptdot_arr); write(fd,buf,len); write(fd," ",1); len = sprintf(buf,"%f",res_cur); write(fd,buf,len); if(i!=quan_tdot-1) { write(fd,"\n",1); } printf("\nf(%f) = %f",*ptdot_arr,res_cur); ptdot_arr++; } ptdot_arr-=quan_tdot; for(i=0;i { free(*pval_arr++); } pval_arr-=quan_dot; free(pval_arr); free(ptdot_arr); close(fd); } #include #include #include #include #include #include "gauss_method.h" #define BUF_SIZE 16 const char path[] = "./canpolin_inter.txt"; void quasivand_constructor(struct Node *,float **,int); void gauss_solution(struct Node *,float **,float *,int); float spow(float ,int); void canpolin_inter(float *,float * ,int, int,int); int main() { int node_quan,i,fd,len; printf("\nInput quantity of nodes : "); scanf("%d",&node_quan); struct Node * p_nodearr = (struct Node *)malloc (sizeof(struct Node)*node_quan); //quasi vandermond pointer float ** p_qvand = (float **)malloc (sizeof(float *)*node_quan); for(i=0;i { *p_qvand++ = (float *)malloc (sizeof(float)*node_quan); } p_qvand-=node_quan; for(i=0;i { printf("\nInput Node[%d].x_value : ",i); scanf("%f",&p_nodearr->x_val); printf("\nInput Node[%d].y_value : ",i); scanf("%f",&p_nodearr++->y_val); } p_nodearr-=node_quan; char buf[BUF_SIZE]; fd = open(path,O_TRUNC|O_WRONLY); for(i=0;i { len = sprintf(buf,"%f",p_nodearr->x_val); write(fd,buf,len); write(fd," ",1); len = sprintf(buf,"%f",p_nodearr++->y_val); write(fd,buf,len); } p_nodearr-=node_quan; quasivand_constructor(p_nodearr,p_qvand,node_quan); gauss_method(p_qvand,p_nodearr,node_quan); float * p_arrcoef = (float *)malloc (sizeof(float)*node_quan); gauss_solution(p_nodearr,p_qvand,p_arrcoef,node_quan); int tdot_quan; printf("\nInput quan of test dots : ");scanf("%d",&tdot_quan); float * p_tdot = (float *)malloc(sizeof(float)*tdot_quan); for(i=0;i { printf("\nInput test_dot[%d] : ",i); scanf("%f",p_tdot++); } p_tdot-=tdot_quan; canpolin_inter(p_tdot,p_arrcoef,tdot_quan,node_quan,fd); for(i=0;i { free(*p_qvand++); } p_qvand-=node_quan; free(p_nodearr); free(p_qvand); free(p_arrcoef); free(p_tdot); close(fd); } //almost vandermond void quasivand_constructor(struct Node * p_arr,float ** p_matrix,int dim) { int i,k; for(i=0;i { for(k=0;k { if(!k) { *(*p_matrix)++ = 1; continue; } *(*p_matrix)++ = spow(p_arr->x_val,k); } *p_matrix-=dim; p_arr++; p_matrix++; } } Полный код можно получить перейдя по ссылке – https://drive.google.com/drive/folders/1RtXObqkX9pVUs_mTSqSTbjcELdH9B6eV?usp=sharing . Результат работы Ожидаемые значения в точках
График 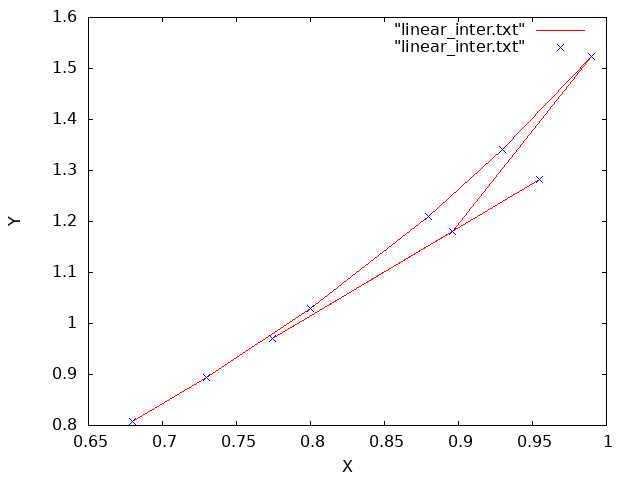   |
