|
|
Комб вероят. Федеральное агентство по образованию Государственное образовательное учреждение
Образец решения варианта
1.Сколькими способами можно расставить на полке 5 различных книг?
Решение. Искомое число способов равно числу перестановок из 5 элементов (книг), т. е. 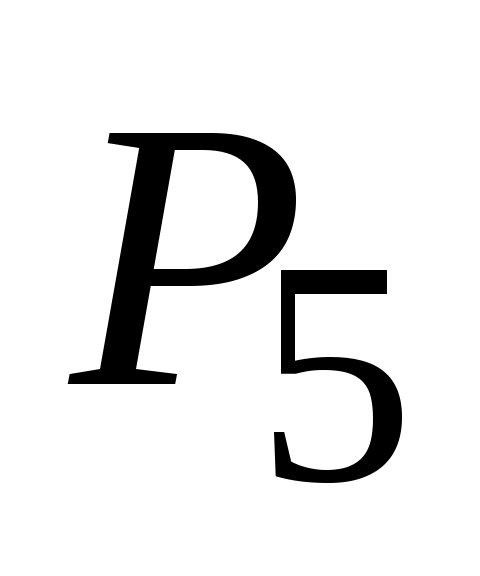 = 5! = 1·2·3·4·5 = 120. = 5! = 1·2·3·4·5 = 120.
2.Сколько «слов» по две буквы можно составить из букв a, b, c, d, e, таким образом, чтобы буквы в «словах» не повторялись?
Решение. Т.к. каждое «слово» должно содержать две буквы, то искомое число способов равно числу размещений из 5 элементов (букв) по две, т. е. 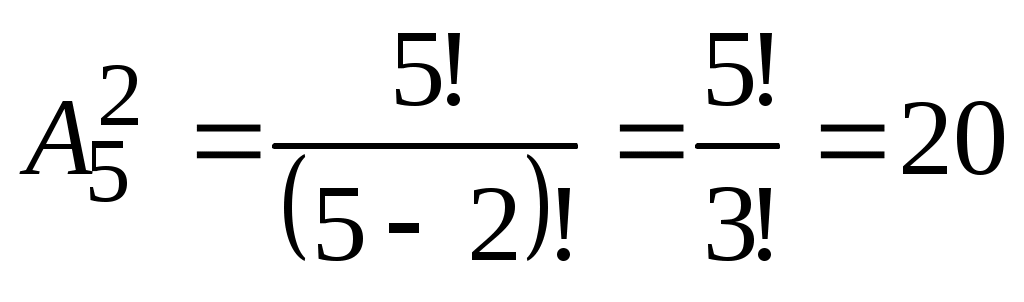 . .
3.Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых из вазы, в которой стоят 10 красных и 4 розовых гвоздики?
Решение. Так как порядок выбора цветов не имеет значения, то красную гвоздику можно выбрать 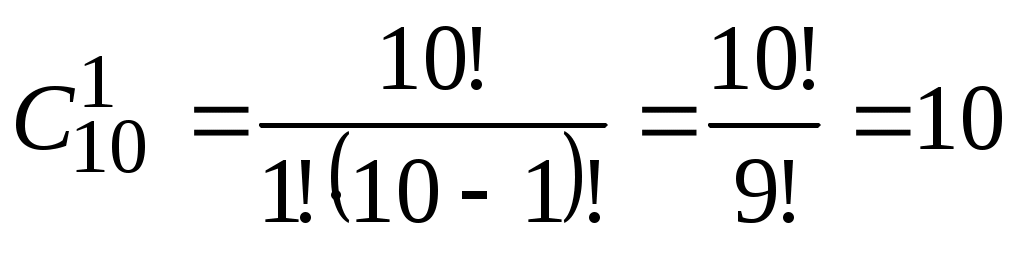 способами. Выбрать две розовые гвоздики из имеющихся четырех можно способами. Выбрать две розовые гвоздики из имеющихся четырех можно 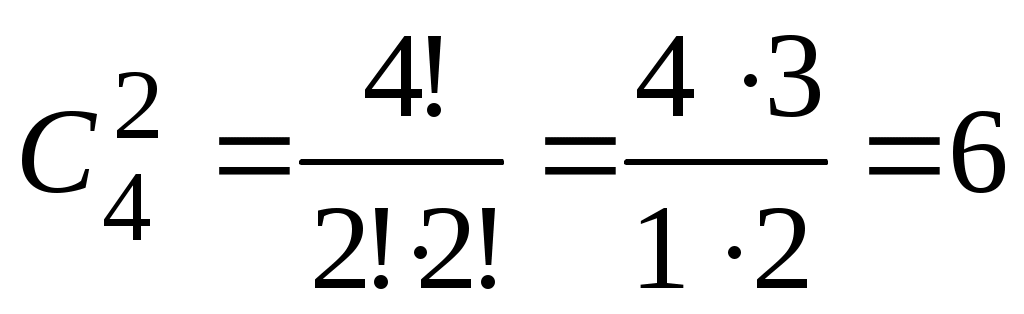 способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения, способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения, 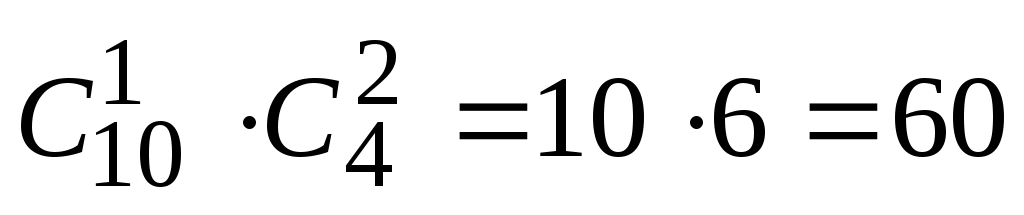 способами. способами.
4. Набирая номер телефона, абонент забыл последние 3 цифры, и помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что номер телефона набран правильно.
Решение. Благоприятствующий исход здесь один – правильный набор последних цифр 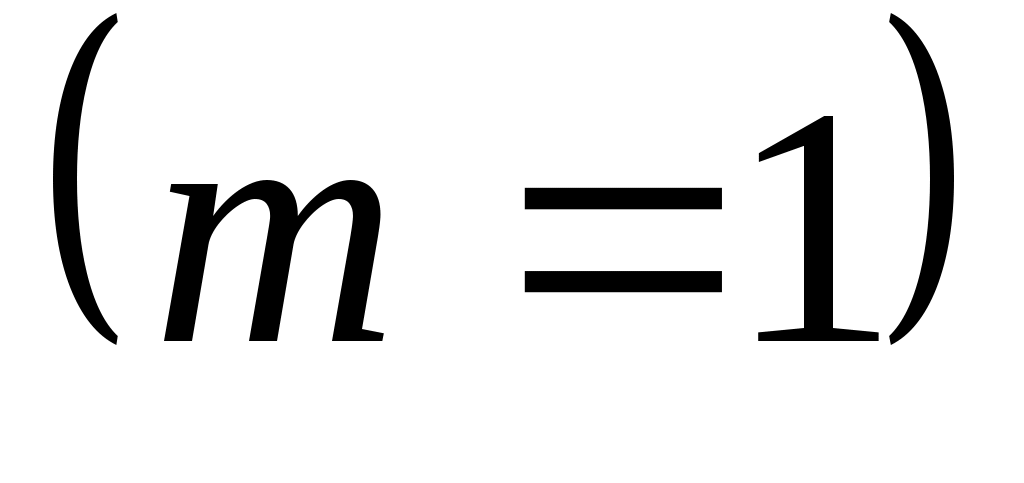 . Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 3 цифр, порядок которых имеет значение, значит . Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 3 цифр, порядок которых имеет значение, значит 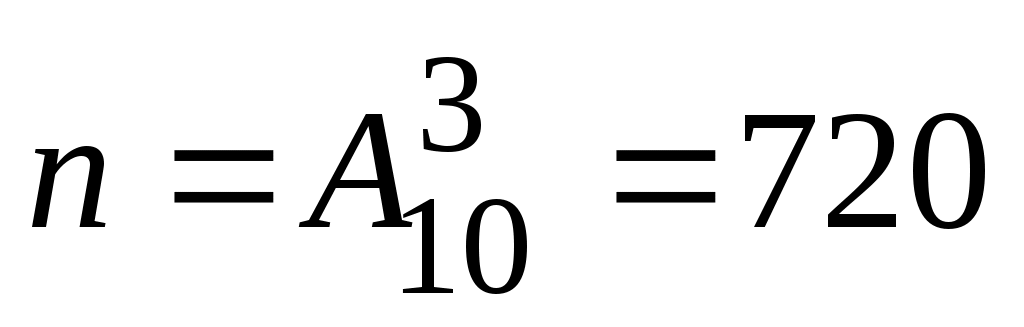 . Значит вероятность того, что номер набран правильно (событие . Значит вероятность того, что номер набран правильно (событие  ): ): 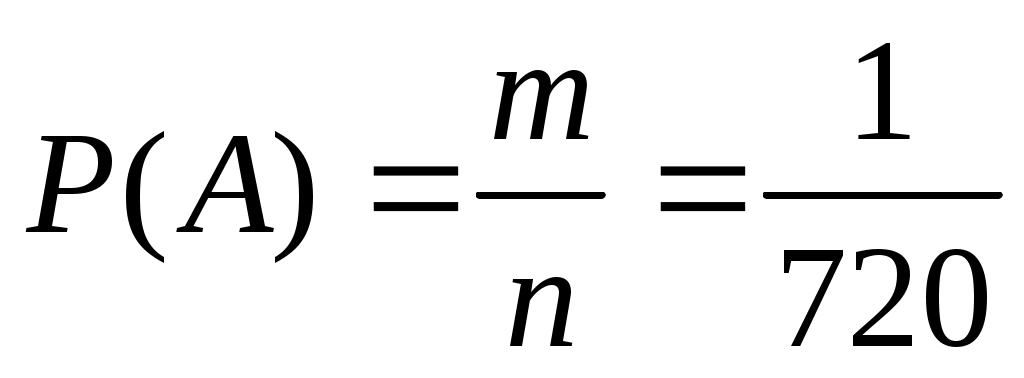 . .
5. Среди 100 колес 5 нестандартных. Для контроля выбирается 7 колес. Найти вероятность того, что среди них ровно 3 будет нестандартных.
Решение. Число всевозможных исходов равно количеству комбинаций из 100 колес по 7 штук, т.к. порядок значения не имеет, то 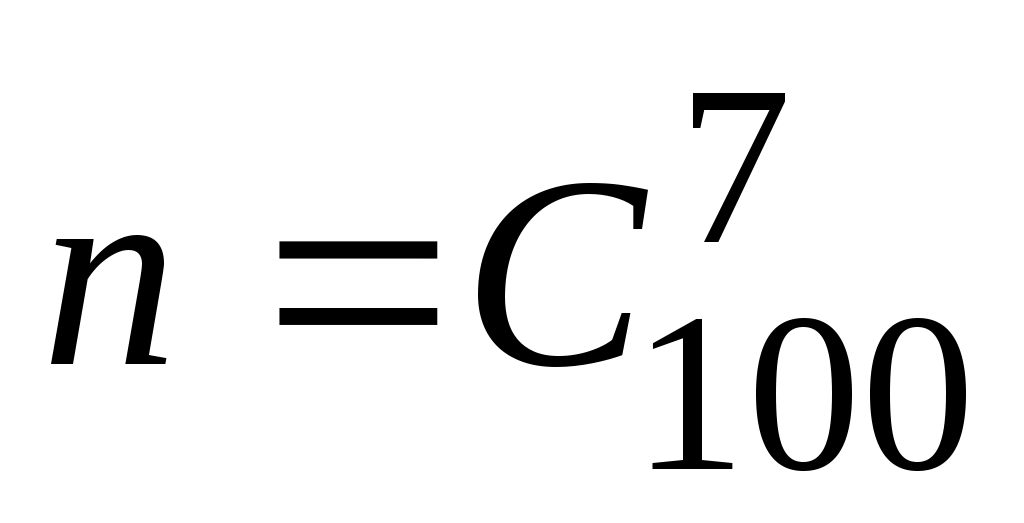 . Благоприятствующий исход состоит в выборе ровно 3 нестандартных колес из 5 и совместном выборе (7-3) стандартных колес из (100-5), порядок значения не имеет. По правилу произведения . Благоприятствующий исход состоит в выборе ровно 3 нестандартных колес из 5 и совместном выборе (7-3) стандартных колес из (100-5), порядок значения не имеет. По правилу произведения 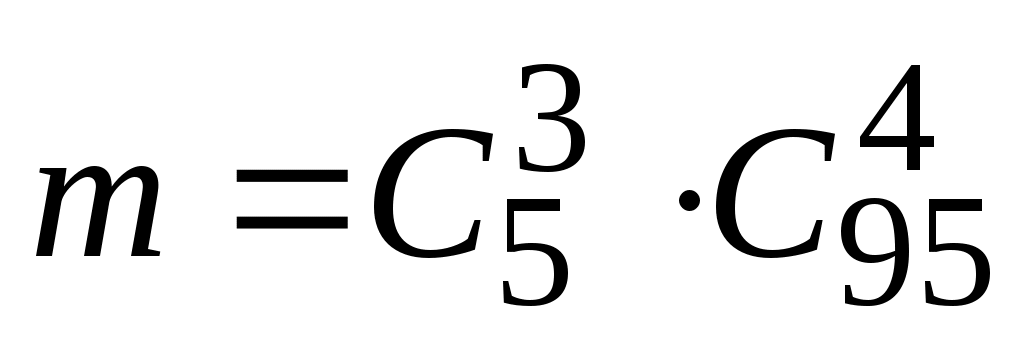 . Следовательно, вероятность того, что среди взятых для контроля колес будет ровно 3 нестандартных (событие . Следовательно, вероятность того, что среди взятых для контроля колес будет ровно 3 нестандартных (событие  ): ): 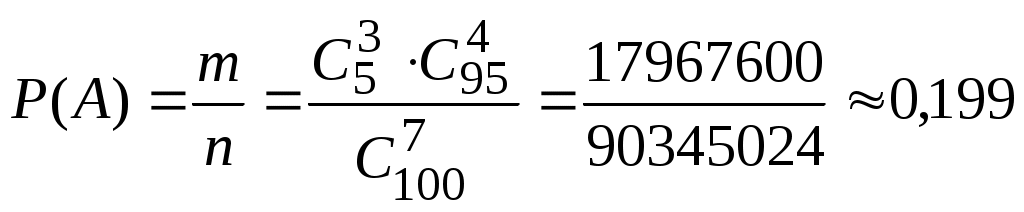 . .
Вариант 1
Сколькими способами можно переставить буквы слова «факультет», таким образом, чтобы две буквы «т» шли подряд?
Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну на левую руку и одну на правую руку так, чтобы они были разных размеров?
Имеются 48 задач по теории вероятностей. Сколькими способами их можно распределить между 13 студентами для самостоятельного решения по 4 задачи каждому?
В ящике 100 болтов диаметром d=4см и 2 болта диаметром d=6см. Наудачу извлекают один болт. Какова вероятность, что он диаметром d=6см?
В коробке 15 книг, среди которых 9 детективов. Наудачу берем 4 книги. Найти вероятность того, что среди них окажется 3 детектива.
|
Вариант 2
Сколько чётных положительных пятизначных чисел можно составить из цифр числа 13754, если каждую цифру можно использовать в записи не более одного раза?
Сколькими способами можно составить трехцветный флаг, если имеется материал пяти различных цветов?
Необходимо доставить рекламные проспекты в 6 различных фирм. Сколькими способами это могут сделать трое курьеров?
В коробке 48 шариковых ручек и 3 гелевых ручки. Наудачу извлекают одну ручку и, не возвращая её обратно, извлекают ещё одну. Какова вероятность, что последняя ручка шариковая, если первая извлеченная ручка – гелевая?
В группе 25 студентов, среди них 5 отличников. Выбирают по списку 10 студентов. Найти вероятность того, что среди них окажется 3 отличника.
| |
|
|
 Скачать 336 Kb.
Скачать 336 Kb. .
.