Федеральное агентство по образованию Государственное образовательное учреждение
 Скачать 0.95 Mb.
|
Федеральное агентство по образованиюГосударственное образовательное учреждениевысшего профессионального образованияПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТНачала анализаИндивидуальные задания
Пермь 2007 Вариант решения заданий Вычислить предел последовательности  .Решение. Распишем факториалы, стоящие в числителе и знаменателе через наименьший, то есть через 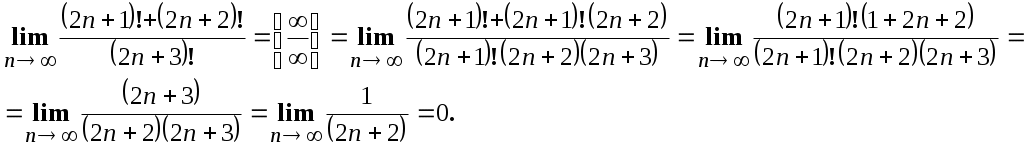 . Ответ. 0.Доказать, что  .Решение. По определению, предел функции  при  равен 7, если для любого  существует такое  , что для всех  из  - окрестности точки  таких, что  справедливо неравенство:  Тогда  . Следовательно, разность между значениями функции и числом 7 меньше  для всех из  окрестности точки . Тем самым утверждение, что доказано.Вычислить пределы функций. А) Найти  Решение. Прежде всего, проверим, применимы ли к данной дроби теоремы о пределах, или мы имеем дело с неопределенностью. Для этого найдем пределы числителя и знаменателя дроби. Функции  и  являются бесконечно большими. Поэтому,  . Следовательно, имеем дело с неопределенностью вида  .Для раскрытия этой неопределенности выделим в числителе и в знаменателе 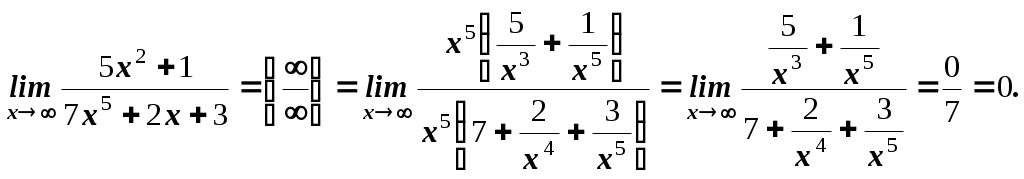в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь. Ответ. 0. Б) Найти  Решение. Для раскрытия неопределенности  в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель. Ответ. -9. В) Найти  .Решение. Для раскрытия неопределенности 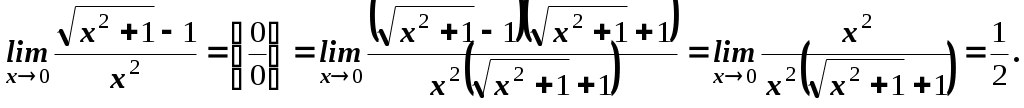в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель. Ответ.  .Г) Найти  Решение. Для раскрытия неопределенности в этом случае, нужно выделить первый замечательный предел:   Ответ. k. Д) Найти  .Решение. Для раскрытия неопределенности 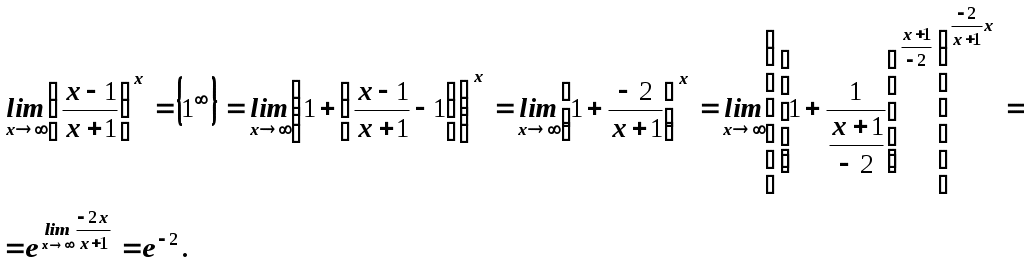 в этом случае, нужно выделить второй замечательный предел: . Ответ.  .Е) Найти  .Решение. Вычисление предела связано с раскрытием неопределенности вида 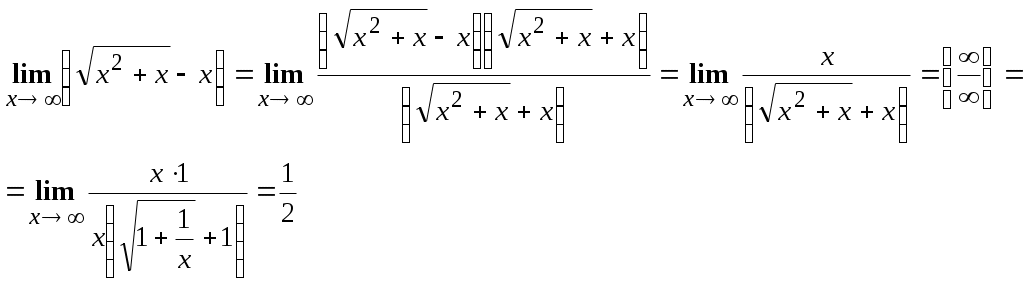 . Для раскрытия этой неопределенности нужно разность преобразовать в частное, то есть неопределенность свести к неопределенности или  . Для этого необходимо избавится от иррациональности. Умножим и разделим выражение  на выражение  и воспользуемся формулой разности квадратов. .Ответ. .Ж) Найти  Решение. Для раскрытия неопределенности 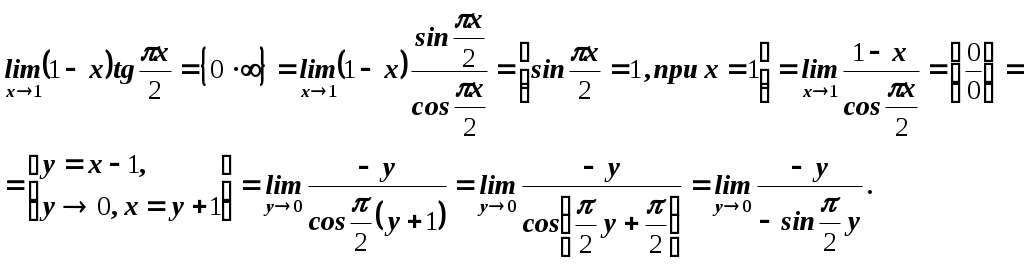 в этом случае, нужно произведение преобразовать в частное, то есть неопределенность свести к неопределенности или . Выделяем первый замечательный предел, то есть умножаем числитель и знаменатель на 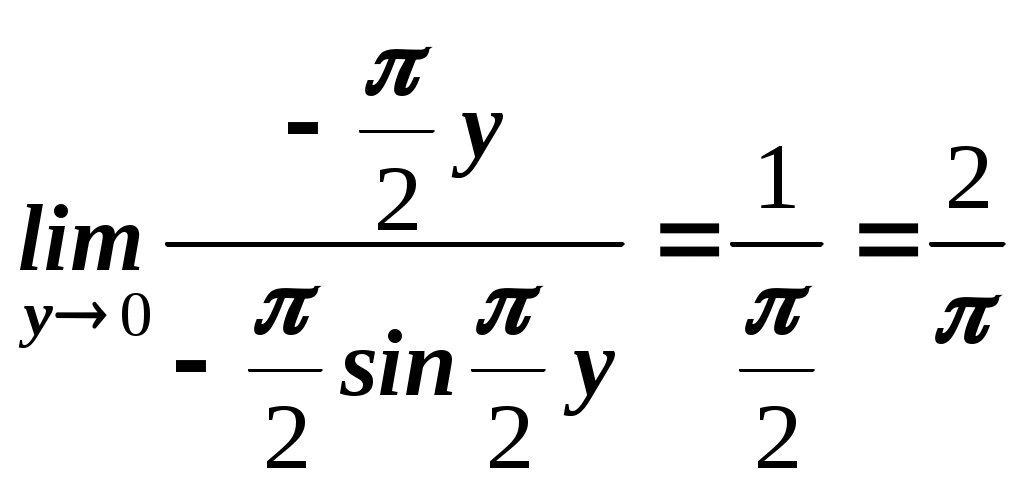 . Получаем, .Ответ.  .З) Найти  Решение. Для раскрытия неопределенности 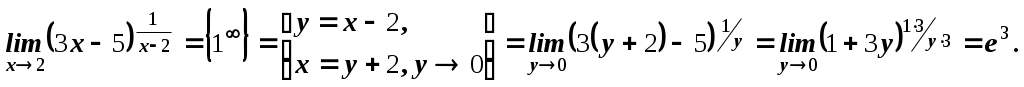в этом случае, нужно выделить второй замечательный предел:  . Ответ.  .И) Найти  .Решение. Для раскрытия неопределенности  , нужно в числителе и в знаменателе выделить множитель  . Для этого числитель и знаменатель разделим на : . = Ответ.  .Указать характер точек разрыва функции  .Решение. Найдем левый и правый предел функции в точке 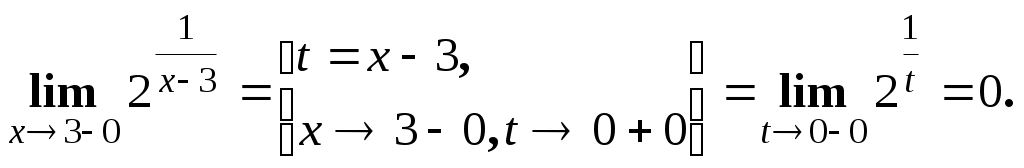 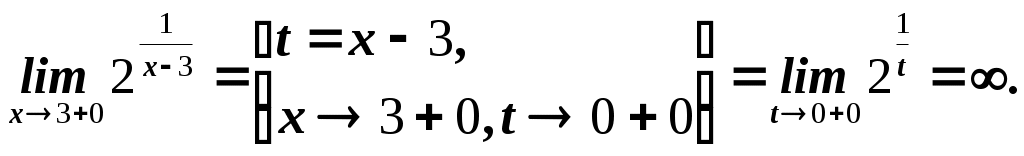.  Левый предел конечен и равен 0, а правый бесконечен. Тогда, по определению, - точка разрыва второго рода.Вариант 1 Вычислить предел последовательности.  .Доказать по определению предела.  .Вычислить пределы функций. а)  ; б)  ;в)  ; г)  ;е)  ; д)  ж)  ; з)  ;и)  .4. Указать характер точек разрыва функции.  .Вариант 2 Вычислить предел последовательности.  .Доказать по определению предела.  .Вычислить пределы функций. а)  ; б)  ;в)  ; г)  ;д)  ; е)  ;ж)  ; з)  ;и)  .4. Указать характер точек разрыва функции.  .Вариант 3 Вычислить предел последовательности.  .Доказать по определению предела.  .3. Вычислить пределы функций. а)  ; б)  ;в)  ; г)  ;д) 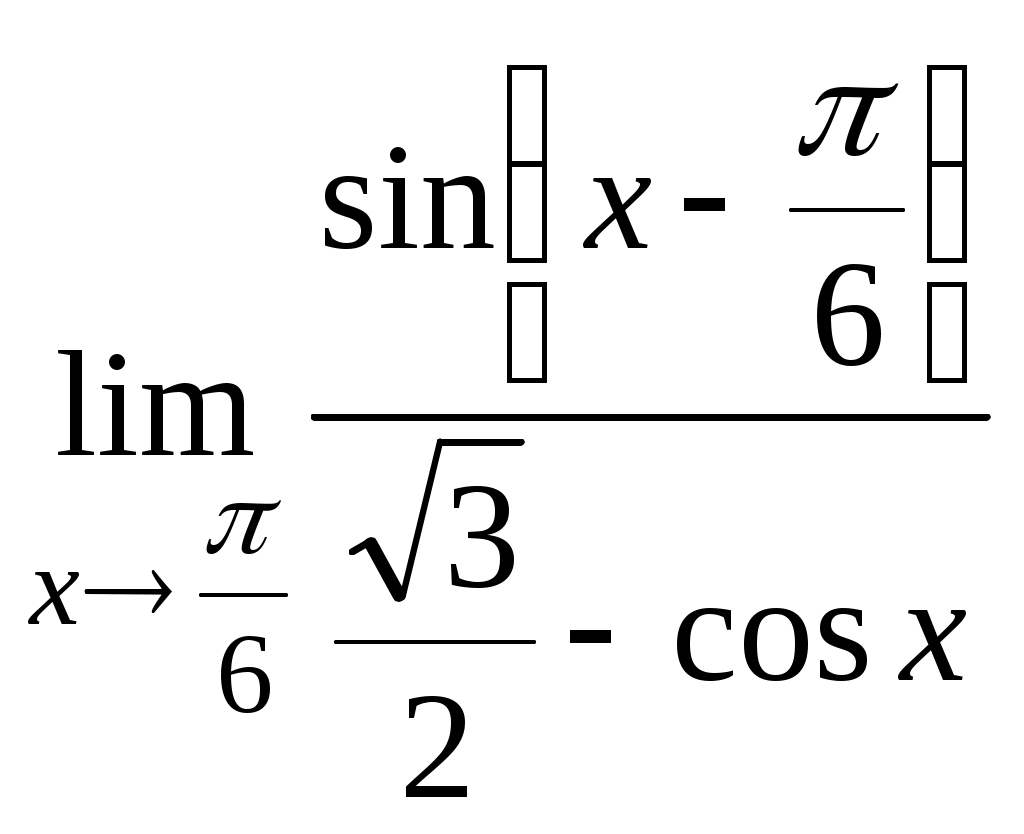 ; е)  ;ж)  ; з)  ;и)  .4. Указать характер точек разрыва функции.  .Вариант 4 Вычислить предел последовательности.  .Доказать по определению предела.  .Вычислить пределы функций. а)  ; б)  ;в)  ; г)  ;д)  ; е)  ;ж)  ; з)  ;и)  .4. Указать характер точек разрыва функции.  . |