контрольная. системный анализ кр. Федеральное государственное бюджетное образовательное учреждение высшего образования Оренбургский государственный аграрный университет
 Скачать 162.97 Kb. Скачать 162.97 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Оренбургский государственный аграрный университет» Шифр студента 2018-210302-08 ФИО Колотаева Валерия Романовна Код направления подготовки/специальности 21.03.02. Направление подготовки/специальность«Землеустройство и кадастры» Курс 3, 32 группа Дисциплина Системный анализ и моделирование Номер контрольной работы 2 ОТМЕТКИ ПРЕПОДАВАТЕЛЯ Фамилия преподавателя Чкалова Марина Викторовна Дата проверки «____»________________ 20___ г. Оценка____________________________________________________________ Подпись преподавателя______________________________________________ Рецензия преподавателя______________________________________________ ____________________________________________________________________________________________________________________________________ Содержание. 1. Понятие системы 2. Структурная схема системы 3. Основные математические модели систем 4. Задания 5. Список используемых источников Понятие системыАнализ системы — это выделение ее частей с целью прояснения состава системы. В предыдущем параграфе мы говорили, что каждая часть системы - это подсистема, и у этой подсистемы есть свои части. Однако невозможно раскладывать систему бесконечно. На чем-то придется остановиться, какие-то части принять за простые, далее неделимые элементы. Вопрос о том, на чем следует остановить «дробление» системы, зависит от цели исследования. Целью исследования системы является получение ее модели - приближенного представления об устройстве и функционировании системы. Полученная модель будет использоваться для прогнозирования поведения системы в некоторых условиях, для управления системой, для диагностики сбоев в функционировании системы и пр. Однако невозможно понять механизм функционирования системы, выяснив только ее состав. Необходимо знать структуру связей между частями системы. Только в совокупности состава и структуры можно понять состояние и поведение системы. Поэтому анализ системы - это первый этап ее исследования. Второй этап называется синтезом. Слово «синтез» означает соединение. Синтез - это мысленное или реальное соединение частей в единое целое. В результате синтеза создается целостное представление о системе, объясняется механизм системного эффекта. Системным анализом называется исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза. Всякое описание системы носит модельный характер, т. е. отражает ограниченное число ее свойств. Модель «черного ящика» В простейшем случае бывает достаточно иметь представление о взаимодействии системы с внешней средой, не вдаваясь в подробности ее внутреннего устройства. Например, при использовании сложной бытовой техники вам совсем не обязательно знать ее устройство. Достаточно знать, как ею пользоваться, т. е. какие управляющие действия можно с ней производить (что на входе) и какие результаты вы будете при этом получать (что на выходе). Все эти сведения содержатся в инструкции для пользователя.. Такое описание системы называется моделью «черного ящика» (рис. 1.2). 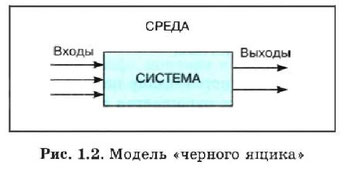 Вход системы - это воздействие на систему со стороны внешней среды, а выход - это воздействие, оказываемое системой на окружающую среду. В такой модели внутреннее устройство системы скрыто. Поэтому ее и называют «черным ящиком». С точки зрения человека, не связанного с системой высшего образования, университет есть «черный ящик», на входе которого - выпускники школ, а на выходе - дипломированные специалисты. Модель состава Как отмечалось выше, результатом анализа системы является определение ее состава. Если описание системы ограничить перечислением ее частей, то мы получим модель состава. Например, модель состава системы «Университет» представлена на рис. 1.3. 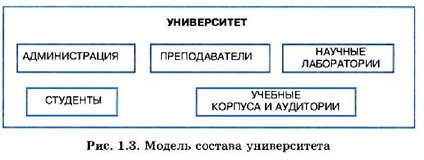 Каждая из отмеченных на рис. 1.3 составляющих системы «Университет» является подсистемой со своим составом. Поэтому для этих подсистем также можно построить свои модели состава. Разумеется, такой модели недостаточно для того, чтобы понять, как функционирует университет. И все-таки она дает более подробное представление об университете, чем модель «черного ящика». Структурная модель системы Структурную модель системы еще называют структурной схемой. На структурной схеме отражается состав системы и ее внутренние связи. Для отображения структурной схемы системы используются графы. Граф состоит из вершин, обозначающих элементы системы, и ребер - линий, обозначающих связи (отношения) между элементами системы. Знакомая многим схема скоростного транспорта Москвы (рис. 1.4) является примером графа. Вершинами здесь являются станции метро, а ребрами - линии движения поездов. Такая схема позволяет пассажиру метро определить маршрут своего перемещения между любыми станциями. Схема метро отражает его радиально-кольцевую структуру. 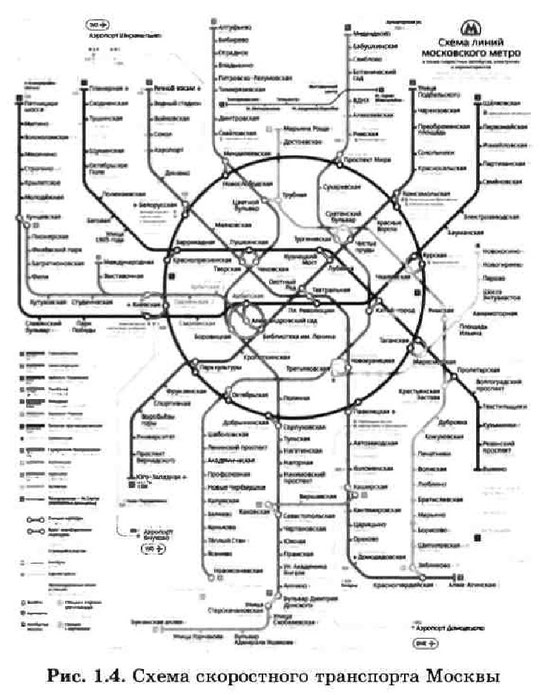 Связь между двумя станциями метро, соединенными линией движения, является двунаправленной, поскольку поезда могут двигаться в обе стороны. Валентная связь между атомами молекулы также не имеет выделенного направления. Такие графы называются неориентированными. Если же связь между двумя элементами системы действует только в одну сторону, то на графе она отображается направленной стрелкой. Такой граф называется ориентированным. Направленные линии связи на графе называются дугами. 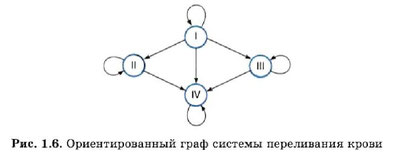 На рис. 1.6 приведен пример ориентированного графа из области медицины. Известно, что у разных людей кровь может различаться по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы. Граф на рис. 1.6 показывает возможные варианты переливания крови. Группы крови - это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания крови одной группы человеку с другой группой. Например, из этого графа видно, что кровь I группы можно переливать любому человеку, а человек с I группой крови воспринимает кровь только своей группы. Видно также, что человеку с IV группой крови можно переливать любую кровь, но его кровь можно переливать только людям с той же группой. 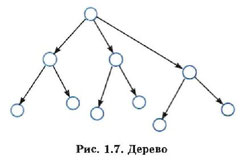 На практике часто встречаются системы с иерархической структурой, граф которых называется деревом (рис. 1. 7). Дерево - это ориентированный граф, хотя при его изображении не всегда рисуются стрелки. Обычно вершины дерева располагаются по уровням сверху вниз. Дуги направлены от верхних вершин к нижним. Каждая вершина может быть связана с одной вершиной верхнего уровня (исходной) и множеством вершин нижнего уровня (порожденными). Такая связь называется «один ко многим". Единственная вершина самого верхнего уровня называется корнем дерева. Вершины самого нижнего уровня, у которых нет порожденных вершин, называются листьями дерева. Дерево является связным графом. Это значит, что между любыми двумя вершинами имеется хотя бы один путь, связывающий их между собой. В дереве отсутствуют петли — замкнутые траектории связей. Поэтому маршрут перемещения по дереву между любыми двумя вершинами всегда является единственным. Структура организации файловой системы во внешней памяти компьютера является иерархической. Вершинами графа, отображающего файловую структуру, являются папки и файлы. Дуги отражают отношения вхождения одних вершин в другие. Дерево имеет многоуровневую структуру. Папка самого верхнего уровня называется корнем дерева. Конечные вершины такого дерева (листья) - это файлы и пустые папки. Задания Отношения эквивалентности # а13б٭ А-множество ключевых слов А2= А*А= {(слово1; слов 2} Rﮯ А2 R: - слова начинающиеся с одинаковых символов R эквивалентности - ? 1) 1 условие – рефлективность. Любое слово находится в отношении само с собой. 2) 2 условие – симметричность а R в =>вR а – условие выполняется 3) 3 условие – транзитивность а R в и в R с => а R с – выполняется Заданное отношение является отношением эквивалентности Элементы теории множеств А= {-1; 0; 1} В= {7;8} А*В= {(-1;7), (-1; 8), (0;7), (0;8), (1;7), (1;8)} В*А= {(7;-1), (7; 0), (7;1), (8;-1), (8;0), (8;1)} А2= {(-1;-1), (-1; 0), (-1;1), (0;-1), (0;0), (0;1),(1;-1), (1;0), (1;1)} В2 = {(7;7), (7;8), (8;7), (8;8)} 3. Примеры нахождения матриц смежности и инцидентности для графа и орграфа Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке. X1 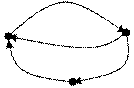 V1 X4 V2 X2 X3 V3 Составим матрицу смежности:
Т. е. 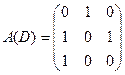 - матрица смежности. - матрица смежности.Матрица инцидентности:
Т. е. 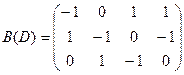 Если граф имеет кратные дуги (ребра), то в матрице смежности принимается Aij=K, где K – кратность дуги (ребра). Пример: Построить матрицы смежности и инцидентности для орграфа D= (V, X) (рис. 1). 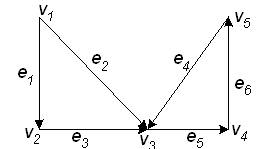 Рис. 1 Орграф для примера Решение. Матрица смежности имеет вид 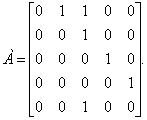 Матрица инцидентности имеет вид  Список использованной литературы https://belledahlia.jimdofree.com/11-класс/учебник-информатика-и-икт-фгос/2-модели-систем-системный-анализ https://function-x.ru/graphs1_relations https://yandex.ru/search/?text=Основные-математические-модели Антонов А.В. Системный анализ. — М.: Высшая школа, 2004. |
