Моделирование процессов и объектов при транспорте и хранении нефти и газа. Моделирование процессов и объектов при транспорте и хранении неф. Федеральное государственное бюджетное образовательное учреждение высшего образования тюменский индустриальный университет

• Название: Федеральное государственное бюджетное образовательное учреждение высшего образования тюменский индустриальный университет
• Анкор: Моделирование процессов и объектов при транспорте и хранении нефти и газа
• Дата: 13.01.2021
• Размер: 160.02 Kb.
• Имя файла: Моделирование процессов и объектов при транспорте и хранении неф.docx
• Тип: Задача; #167848

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»

«Основы строительства и эксплуатации систем транспорта и хранения углеводородов»

Выполнил:

студент гр.

Тюмень, 2020

Моделирование процессов и объектов при транспорте и хранении нефти и газа

Цель работы получение навыков моделирования параметров технологических процессов в оборудовании и трубопроводах.

Задачи работы:

1. Изучить теоретические основы, методику оценки, регламенты и инструкции (при наличии);

2. Составить алгоритм оценки и выполнить расчёт;

3. Проанализировать результаты расчетов, предложить альтернативное решение.

Выполнить комплекс расчетов

Задача 1

Молярная масса газа равна M. Определить его плотность при t °С и абсолютном давлении p.

№ варианта	M	t, °С	p, Па
9	18	210	9,01 · 104

Решение

Плотность газа при 0 °С и 1 атм может быть определена по его молярной массе М

ρ = 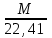= 18/22,41 = 0,803 кг/м³,

где 22,41 м³ – объем одного моля любого газа при 0 °С и 1 атм.

Пересчет плотности с одних параметров состояния на другие можно произвести по формуле

ρ₂ = ρ₁ ,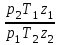

где p₁ и p₂ – абсолютные давления газа; T₁ и T₂ – абсолютные температуры газа; z₁ и z₂ – коэффициенты сжимаемости газа, для идеального газа принимаем, z = 1.

ρ₂ = 0,803 · 9,01·10⁴·273,15·1/101325·(210+273,15)·1= 0,403 кг/м³.

Ответ: ρ₂ = 0,403 кг/м³.

Задача 2

Определить абсолютную плотность газовой смеси при следующем объемном составе: А % метана, В % этана и С % пропана при стандартных условиях и относительную плотность смеси по воздуху.

Молярные массы: Плотности при 20 °С и 1 атм

метан 16,043 0,717

этан 30,07 1,344

пропан 44,097 1,967

воздух 28,96 1,206

№ варианта	А	В	С
9	78	14	8

Решение

Плотность газовой смеси определяется по правилу смешения

ρ_см = a₁ρ₁ + a₂ρ₂ + a₃ρ₃ + … + a_nρ_n,

где a₁, a₂, a₃, a_n – объемные концентрации компонентов смеси;

ρ₁, ρ₂, ρ₃, ρ_n – плотности компонентов смеси.

ρ_см = 0,78 · 0,717 + 0,14 · 1,344 + 0,09 · 1,967 = 0,924 кг/м³.

Относительная плотность газа

Δ = 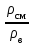= 0,924/1,206 = 0,766

где ρ_в = 1,206 кг/м³ – плотность воздуха.

Плотность газовой смеси можно определить и по молярной массе

Δ = = = =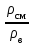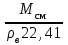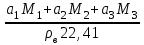

= 0,78·16,043+0,14·30,07+0,09·44,097/1,206·22,41= 0,765

Ответ: Δ = 0,765

Задача 3

Газ относительной плотностью 0,75 при температуре t °С и давлении p МПа занимает объем V м³. Определить его объем для стандартных условий и при 20 °С и атмосферном давлении. Коэффициент сжимаемости принять равным 0,95.

№ варианта	V, м3	t, °С	p, МПа
9	280	50	1,0

Решение

Абсолютное давление газа

p = 1,0 · 10⁶ + 101325 = 1,101325 · 10⁶ Па.

Абсолютная температура газа

T = 273,15 + 50 = 323,15 К.

Приведение объема газа к нужным параметрам выполняется по следующей зависимости

V₂ = V₁ .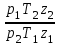

Тогда объем для стандартных условий (T₂ = 273,15 (0 °С) и p₂ = 1 атм = 101325 Па)

V₀ = V₁ 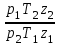= 280 · 1,101325 ·10⁶·273,15/101325·323,15·0,95 = =2707,8 м³.

Объем при 20 °С (T₂ = 273,15 + 20 = 293,15 К) и атмосферном давлении

V₂₀ = V₁ 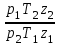= 280 ·1,101325 ·10⁶·293,15/101325·323,15·0,95 = =2906,1 м³.

Ответ: V₀ =2707,8 м³; V₂₀ = 2906,1 м³.

Задача 4

62 кг жидкого газа имеет массовый состав: А % пропана, В % бутана, С % пентана. Определить объем газа после его испарения при 0° и атмосферном давлении.

Молярные массы:

пропан 44,097

бутан 58,124

пентан 72,151

№ варианта	А	В	С
9	78	14	8

Решение.

Если известен массовый состав газовой смеси в процентах, то его средняя молярная масса может быть определена по формуле

M_ср = ,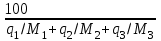

где M₁, M₂, M₃ – молярные массы компонентов смеси;

q₁, q₂, q₃ – массовый состав компонентов в процентах.

M_ср = 100/78/44,097+14/58,124+8/72,151=47,15
Объем газа после испарения

V = 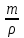= = 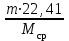62·22,41/47,15 = 29,46 м³,

где 22,41 – объем одного киломоля лютого газа при 0° и атмосферном давлении, м³.

Ответ: V = 29,46 м³.

Задача 5

В вертикальном цилиндрическом резервуаре диаметром d = 4 м хранится m = 92 тонн нефти, плотность которой при 0 °С составляет ρ₀ = 870 кг/м³. Определить колебание уровня в резервуаре при колебании температуры нефти от 0 °С до t = 34 °С. Расширение резервуара не учитывать. Коэффициент теплового расширения принять равным β_Т = 0,00072 1/град.

Решение

Объем нефти в резервуаре

W₁ = 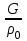= 92·10³/870= 105,74 м³.

Увеличение объема нефти при повышении температуры на Δt = t₂ –t₁:

ΔW = W₁ · β_Т · Δt= 105,74 · 0,00072 · (34 – 0) = 2,58 м³

Колебание уровня нефти в резервуаре

Δh = 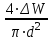= 4·2,58/3,14·4² = 0,205 м = 205 мм.

Ответ: Δh = 205 мм.

Задача 6

Винтовой пресс Рухгольца (рис. 1) для тарировки пружинных манометров работает на масле с коэффициентом сжимаемости β_p = 0,638 · 10^-9 Па^-1. Определить, на сколько оборотов надо повернуть маховик винта, чтобы поднять давление на p = 11,0· 10⁴ Па, если начальный объем рабочей камеры пресса V = 0,630 · 10^-3 м³, диаметр плунжера d = 0,029 м, шаг винта h = 2 мм. Стенки рабочей камеры считать недеформируемыми.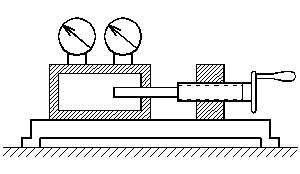



Рис. 1

Решение

Давление в рабочей камере пресса повышается вследствие уменьшения объема масла при поступательном движении плунжера.

Изменение объема масла ΔV при повышении давления в камере на величину Δp можно найти из выражения для коэффициента объемного сжатия β_p

β_p = ;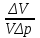

ΔV = β_pVΔp = 0,638·10^-9·0,630·10^-3·11,0·10⁴ = 44,213 · 10^-9 м³.

Длина l, на которую должен продвинуться плунжер, равна

l = 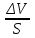= =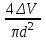4·44,213·10^-9/3,14·0,029² = 66,97 · 10^-6 м.

где S – площадь поперечного сечения плунжера.

При этом маховик винта необходимо повернуть на

n = 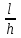= 66,97·10^-6 /0,002 = 0,0334 об.

Ответ: n = 0,0334 об.

Задача 7

В закрытом резервуаре с нефтью плотностью ρ = 845 кг/м³ вакуумметр, установленный на его крыше, показывает р_в = 1,21 · 10⁴ Па (рис. 2). Определить показание манометра р_м, присоединенного к резервуару на глубине H = 6 м от поверхности.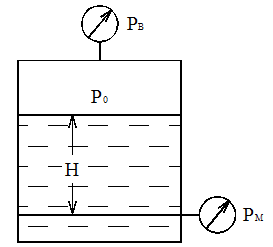


Рис. 2

Решение

Определим давление на свободной поверхности жидкости в закрытом резервуаре. Так как вакуумметр показывает вакуумметрическое давление, то на поверхности жидкости в резервуаре давление тоже будет вакуумметрическое

р₀ = р_в.

Запишем уравнение давления на глубине H от поверхности нефти в резервуаре (в месте установки манометра)

р_м = – р₀ + ρgH.

Тогда показание манометра составит

р_м = – р₀ + ρgH = – 1,21 · 10⁴ + 845 · 9,81 · 6 = 37636 Па = 37,63 кПа.

Ответ: р_м = 37,63кПа.

Задача 8

Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двух жидкостного манометра (рис. 3). Высоты столбиков ртути равны соответственно h₁ = 78 см, h₂ = 42 см, h₃ = 64 см, h₄ = 37 см, h₅ = 100 см. Плотность воды равна ρ = 1000 кг/м³. Плотность ртути ρ_рт = 13600 кг/м³.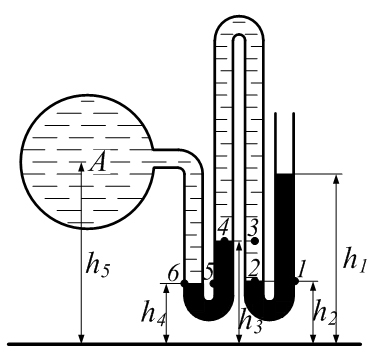


Рис. 3

Решение

Так как жидкость находится в равновесии, то давления в точке 1 и в точке 2 равны как давления в точках одного и того же объема однородной покоящейся жидкости, расположенных на одной горизонтали, т. е. p₁ = p₂. На том же основании p₃ = p₄, p₅ = p₆. В то же время избыточное давление

p₁ = ρ_ртg(h₁ – h₂);

p₃ = p₂ – ρg(h₃ – h₂);

p₅ = p₄ + ρ_ртg(h₃ – h₄);

p_А = p₆ – ρg(h₅ – h₄).

Исключив из этих соотношений промежуточные давленияp₂, p₄, p₆, получим

p_А = ρ_ртg[(h₁ – h₂) + (h₃ – h₄)] – ρg[(h₃ – h₂) + (h₅ – h₄)] =

= 13600 · 9,81 · [(0,78 – 0,42) + (0,64 – 0,37)] –

– 1000 · 9,81 · [(0,64 – 0,42) + (1,00 – 0,37)] = 75713,5 Па = 75,71 кПа.

Ответ: p_А = 75,71кПа.

Задача 9

Определить давление на забое закрытой газовой скважины (рис. 4), если глубина скважины H = 200 м, манометрическое давление на устье p_м = 10,6 Па, плотность природного газа при атмосферном давлении и температуре в скважине (считаемой неизменной по высоте) ρ = 0,69 кг/м³, атмосферное давление p_а = 98 кПа.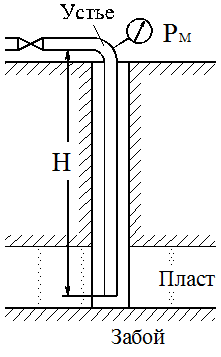


Рис. 4

Решение

Для определения давления на забое газовой скважины воспользуемся барометрической формулой

p = p₀ .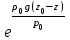

В нашей задачеp₀ – абсолютное давление газа на устье скважины

p₀ = p_а + p_м = 98000 + 10,6= 98010,6 Па;

ρ₀ – плотность при давлении p₀;

z₀ – z = H = 200 м.

Из уравнения состояния газа следует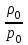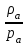

= = 0,69/98000 = 7,040 · 10^-6 с²/м²,

а показатель степени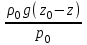

= 7,040 · 10^-6 · 9,81 · 200 = 0,0138.

Тогда p = 98010,6 · e^0,0138 = 99373 Па.

Ответ:p = 99373 Па.

Задача 10. Определить скорость выхода струи пара из сопла паровой турбины, если каждый килограмм пара   при расширении уменьшает свою внутреннюю энергию на  . Принять начальную скорость пара   на входе в сопло, равную нулю.

U=480000 Дж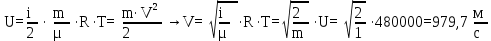