Лабораторная по ИС. Федеральное государственное бюджетное образовательное учреждение высшего образования новосибирский государственный технический университет
 Скачать 2.3 Mb. Скачать 2.3 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра систем сбора и обработки данных ОТЧЁТ по лабораторной работе №6 «Кодирование данных на физическом уровне» по дисциплине: Информационные сети
Новосибирск 2022 Цель работы Изучение кодирования данных на физическом уровне. Рассмотрение различных методов кодирования. Сравнение эффективности методов кодирования. Ход работы В данной работе зададим сигнал NRZ в виде вектора значений. Из него получим остальные виды сигналов: 2B1Q, AMI, биполярный импульсный и манчестерский. Произведём сравнение амплитудных спектров данных сигналов со спектром меандра. Произведём процедуру восстановления исходного сигнала при ограниченном числе гармоник в частотной области. После чего рассчитаем погрешности при восстановлении сигналов. Н 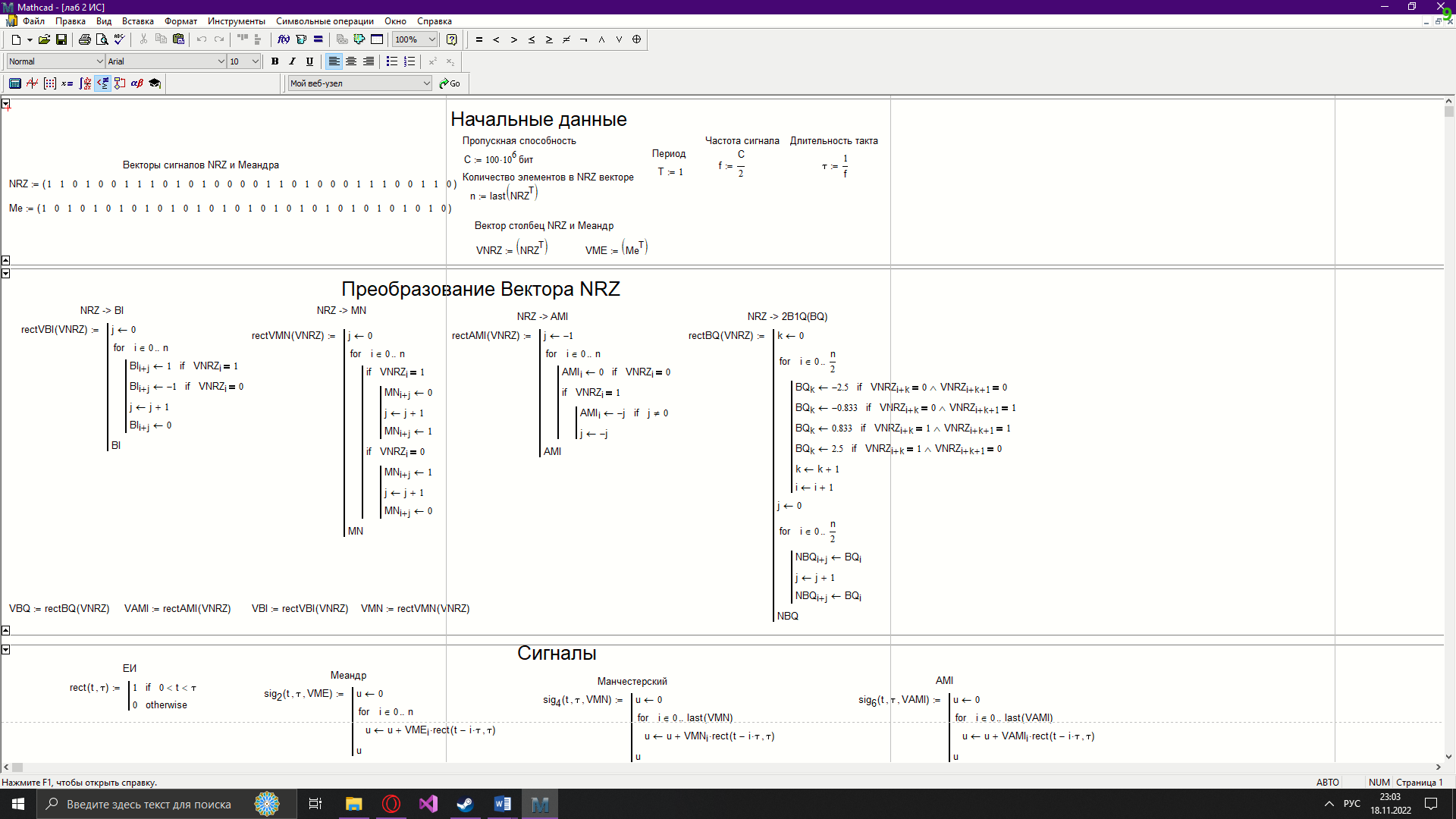 ачальные данные ачальные данныеФункции преобразование вектора NRZ в другие кодировки Данные функции предназначены для преобразования вектора значений сигнала NRZ в соответствующие вектора значений других кодировок. 1)Функция преобразования вектор-значения NRZ в 2B1Q. Вектор в два раза короче, т.к. два такта исходного кодируются одним четырехуровневым. 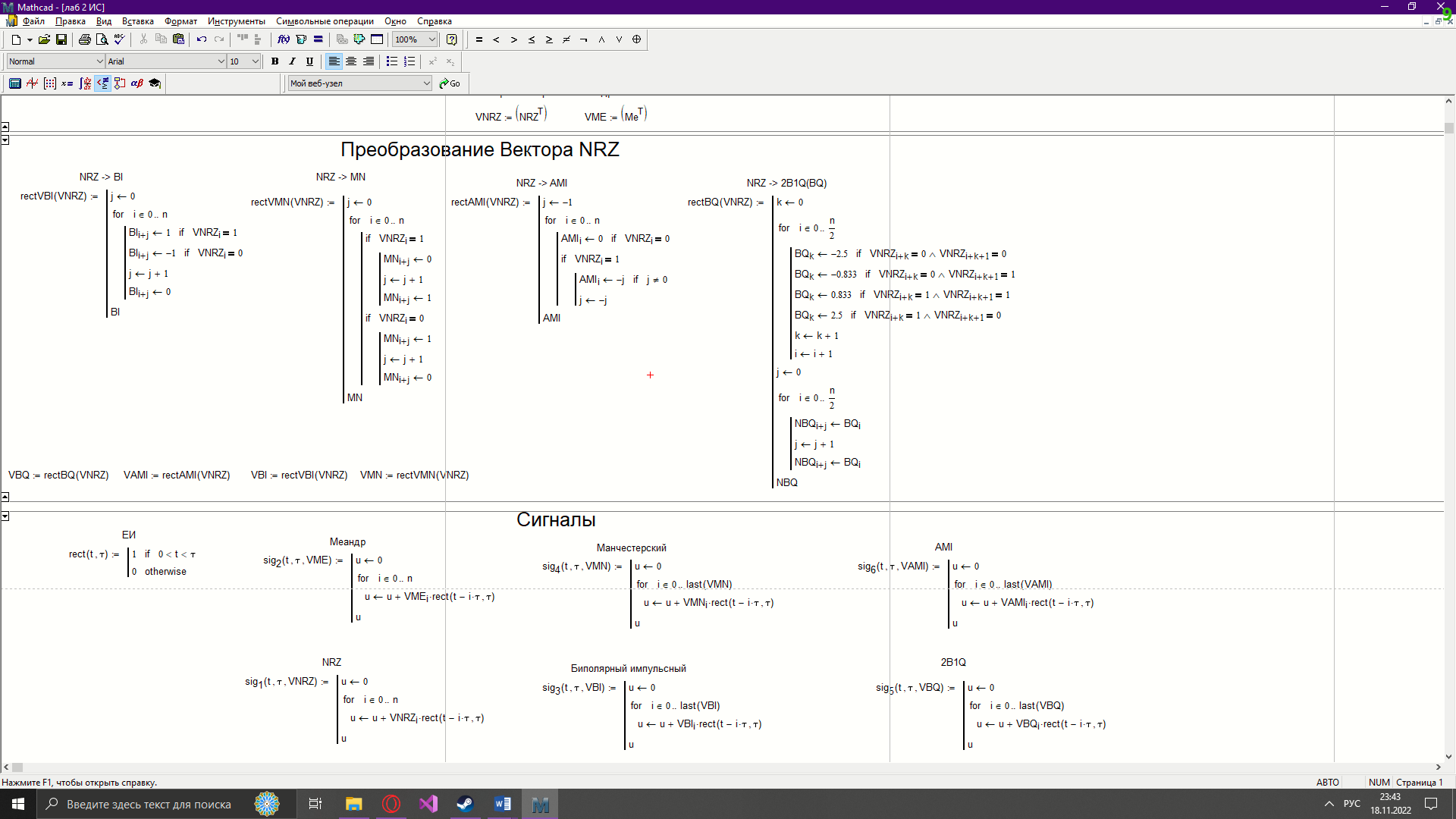 2) Функция преобразования вектор-значения NRZ в вектор значений биполярного импульсного(BI). 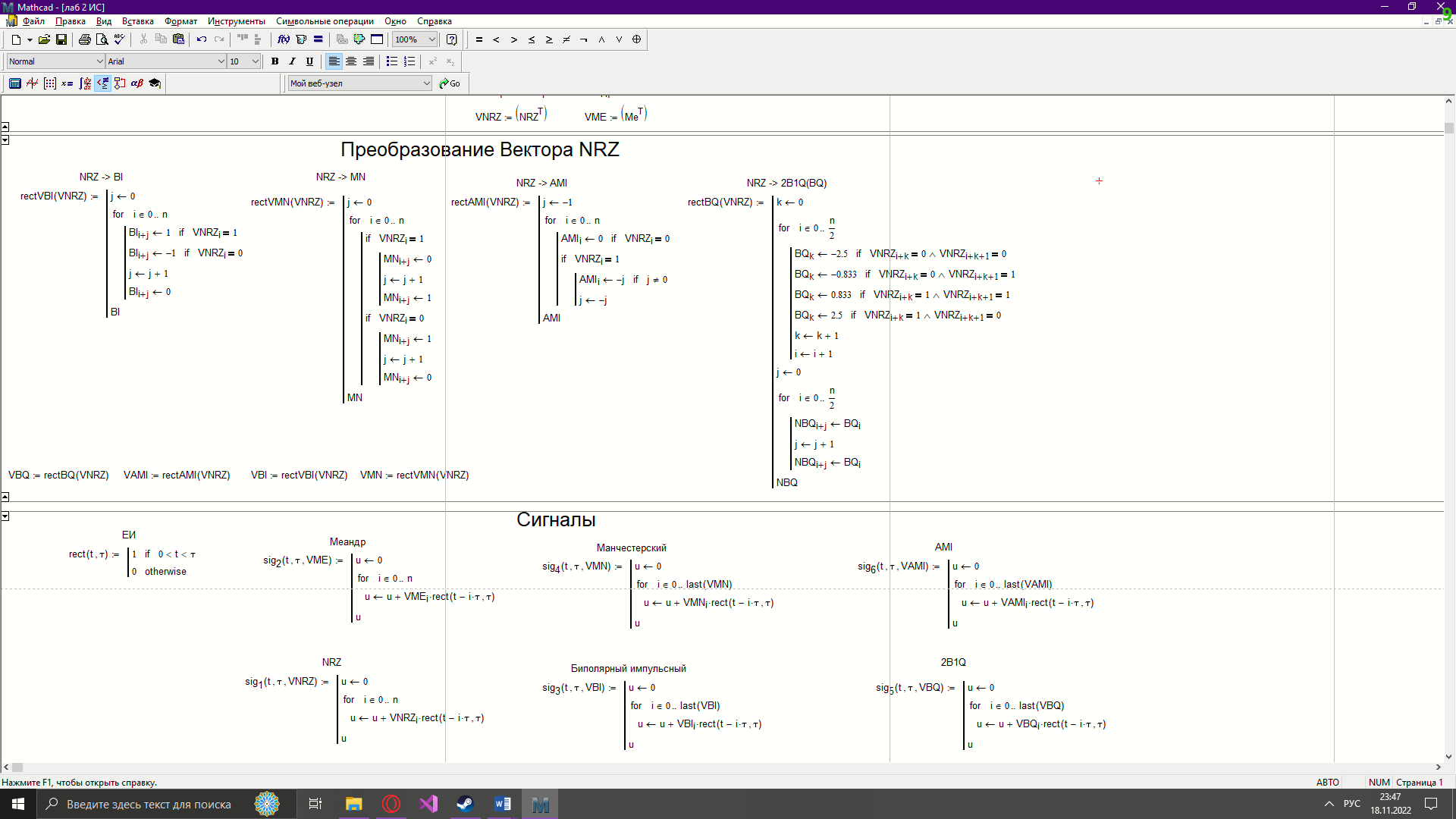 3) Функция преобразования вектор-значения NRZ в AMI. Длина остается прежней. 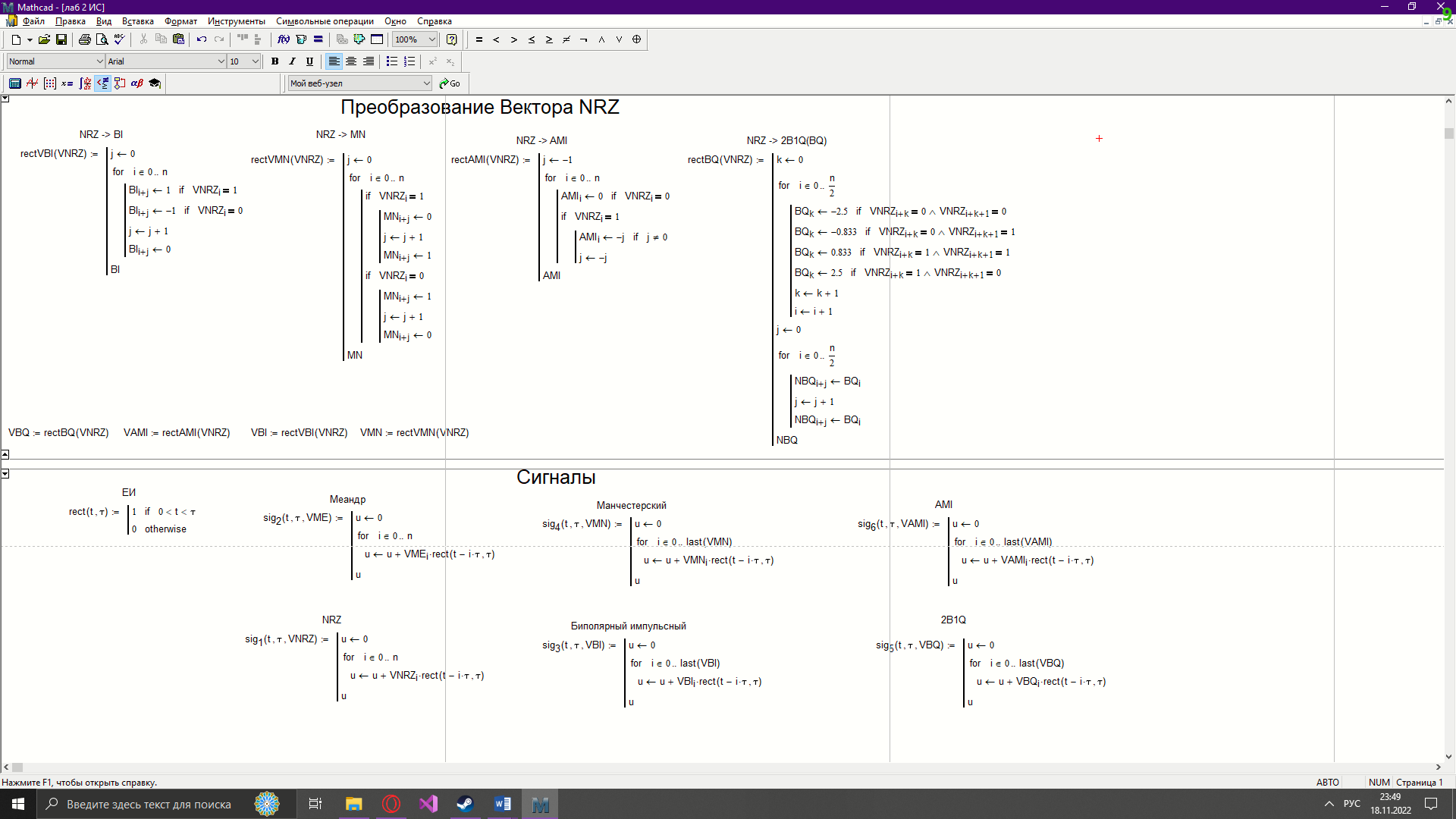 4) Функция преобразования вектор-значения NRZ в вектор значений манчестерского(MN). 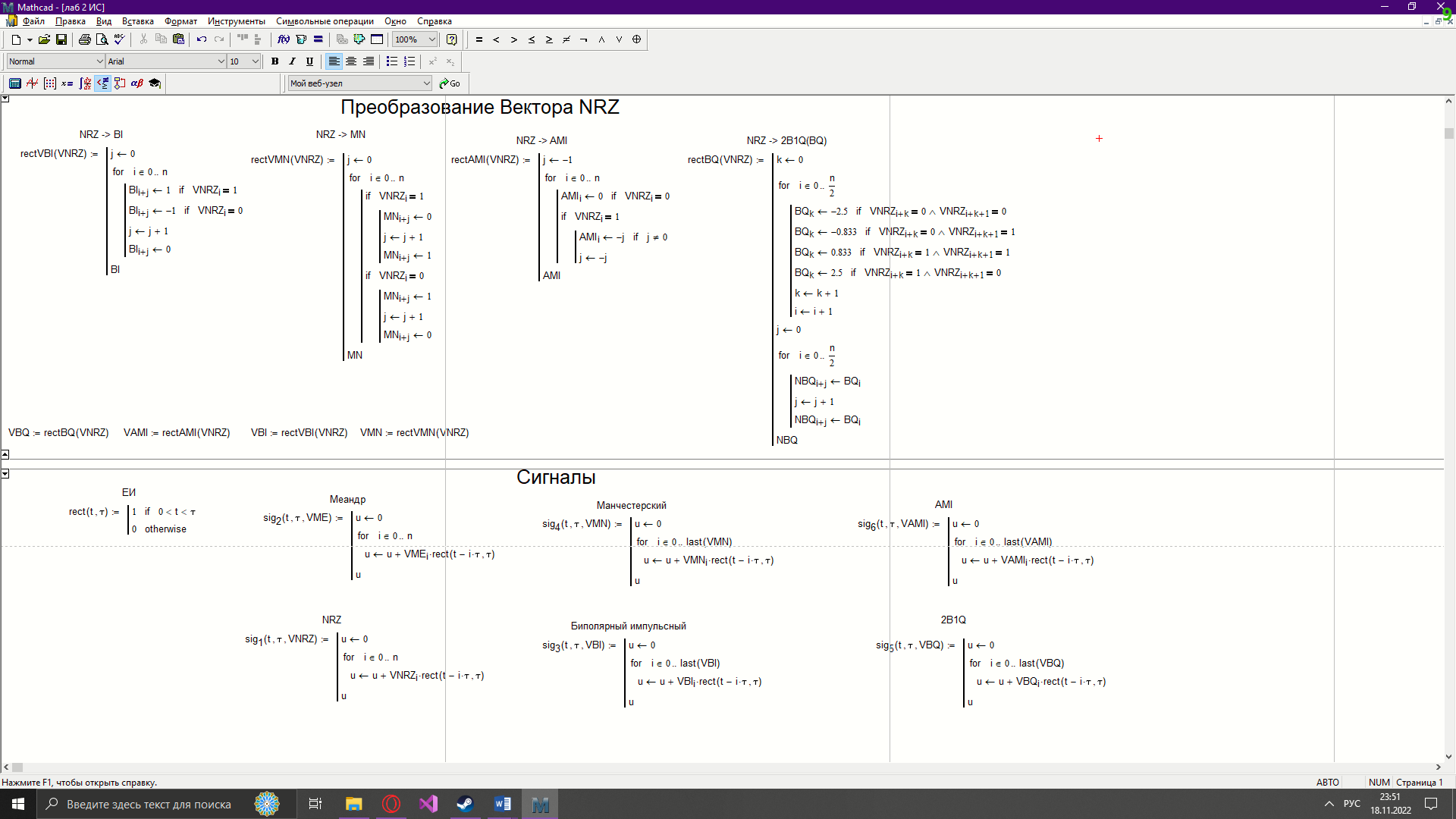 Модуляция сигналов 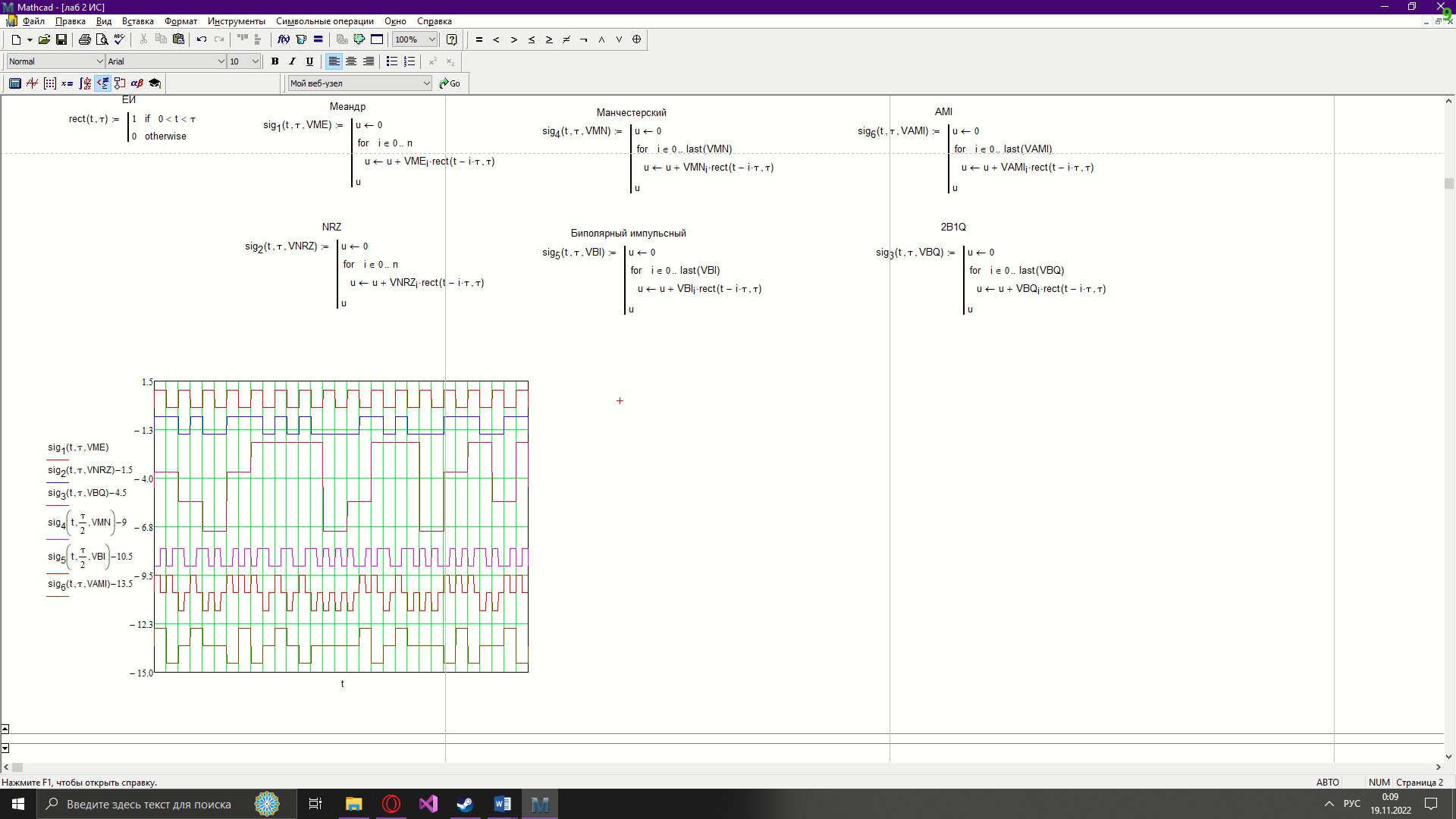   Передискретизация На один такт приходится 32 отсчета 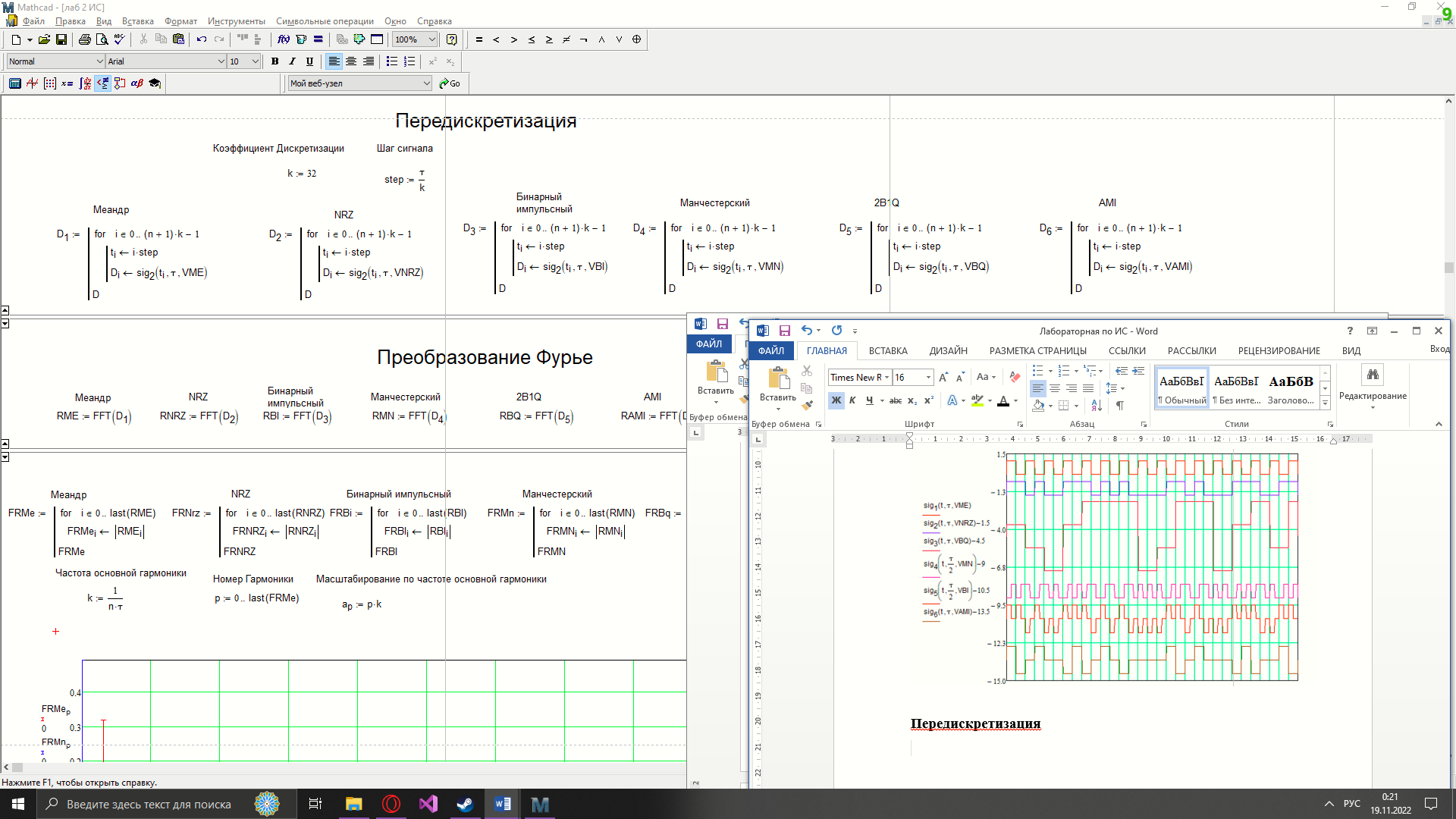   Работа с меандрическим сигналом. Преобразования фурье 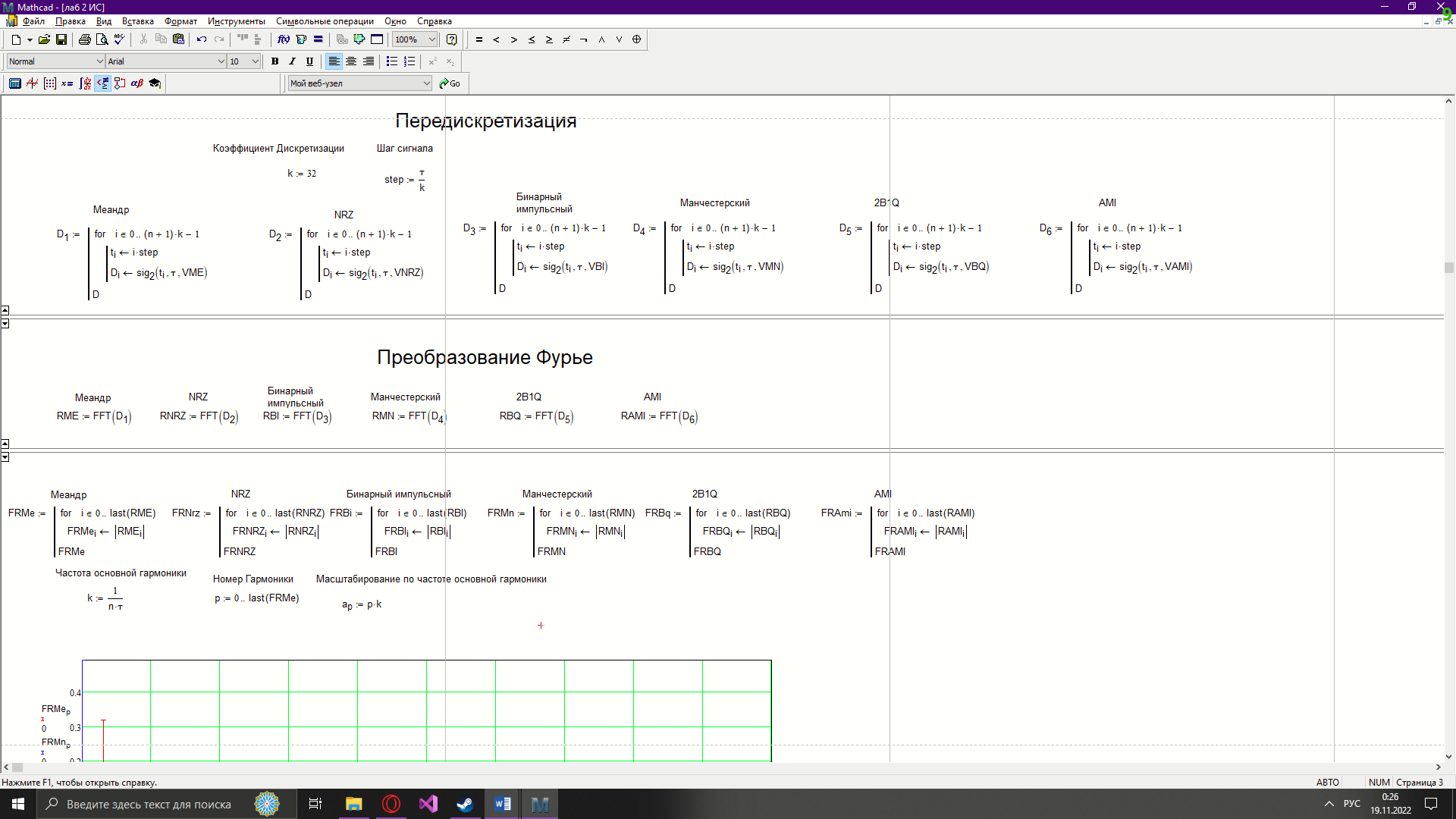   Получение амплитудного спектра 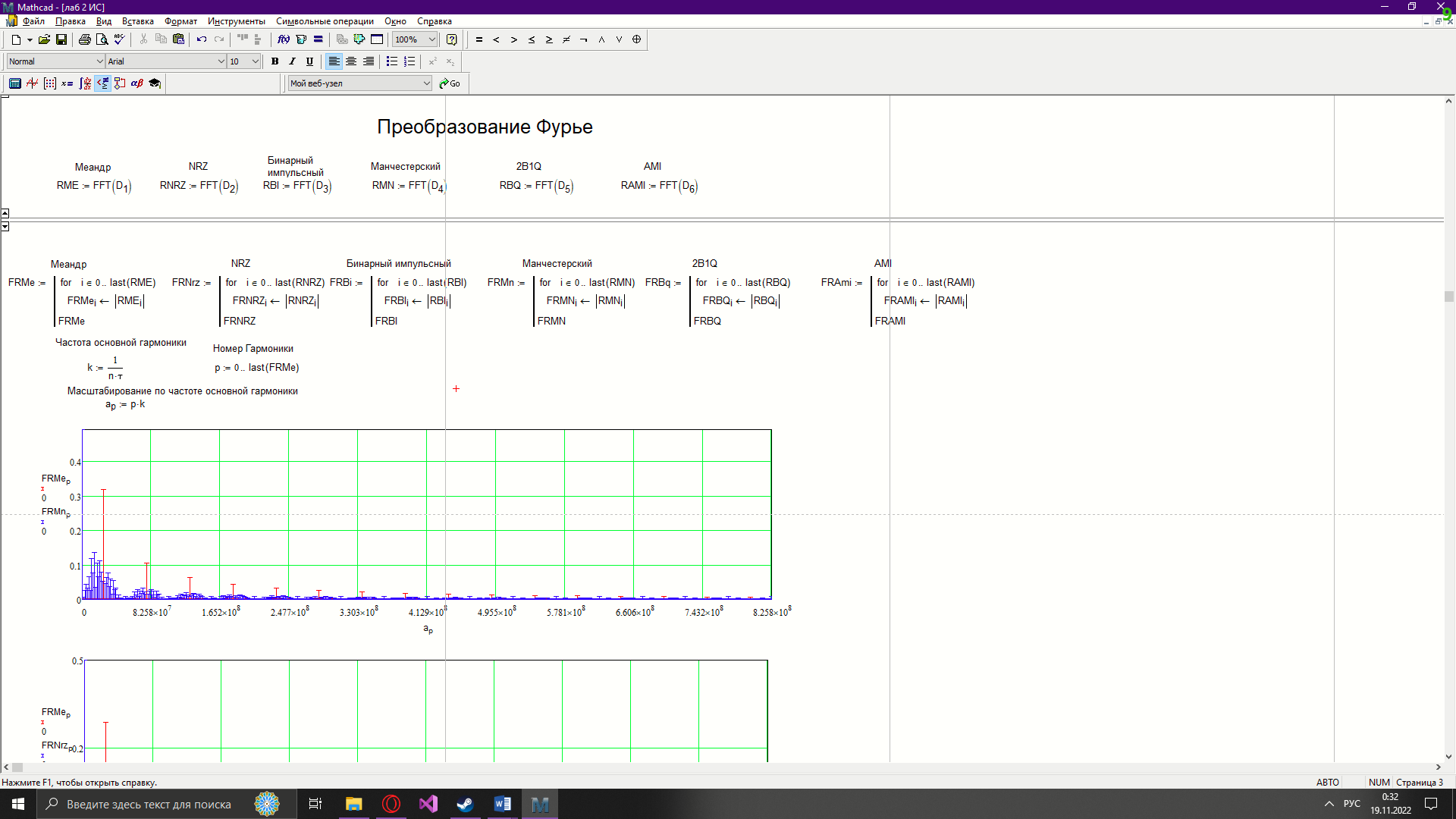   С 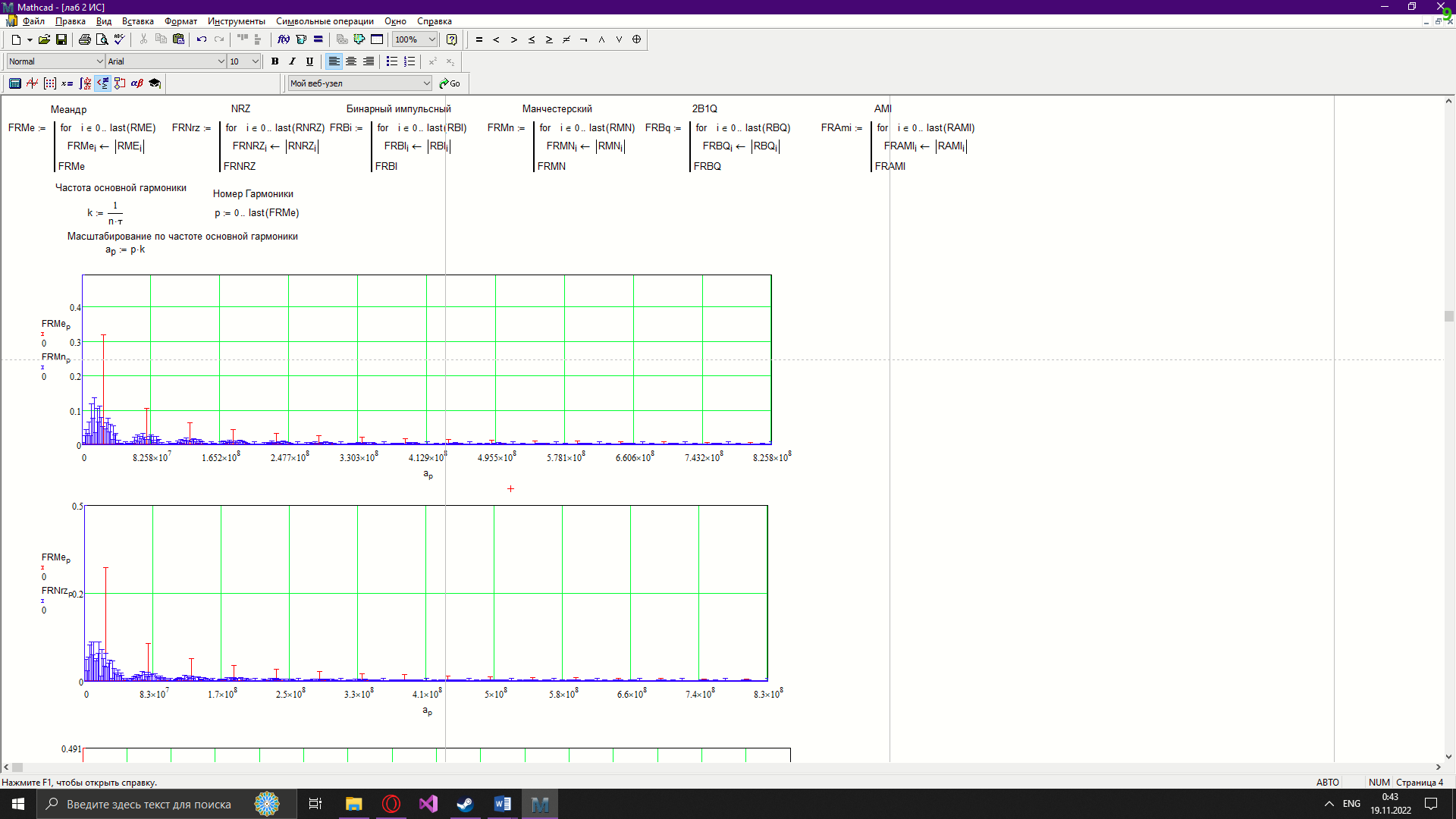 равнение спектров меандра и NRZ равнение спектров меандра и NRZС 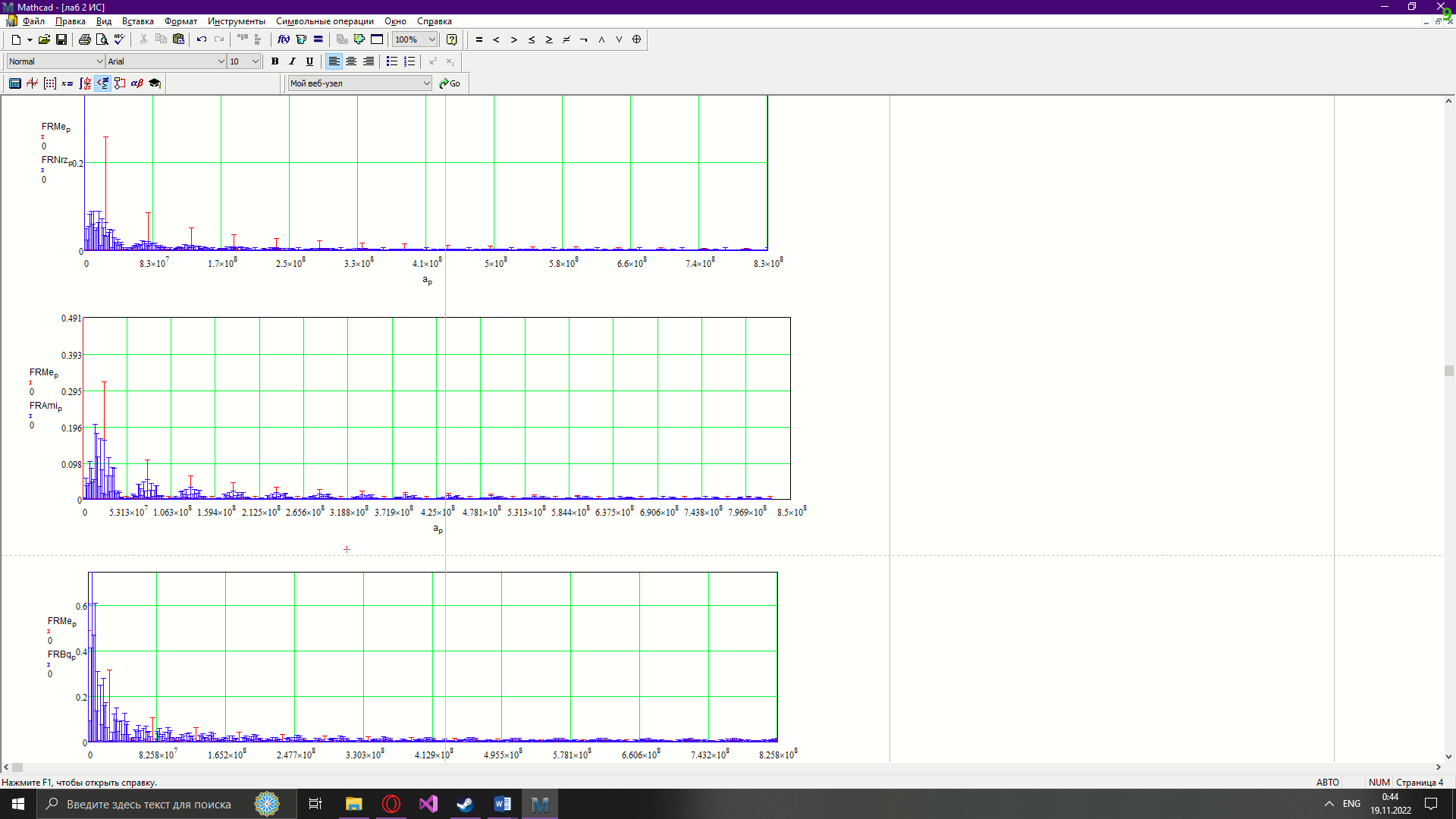 равнение спектров меандра и 2B1Q равнение спектров меандра и 2B1QС 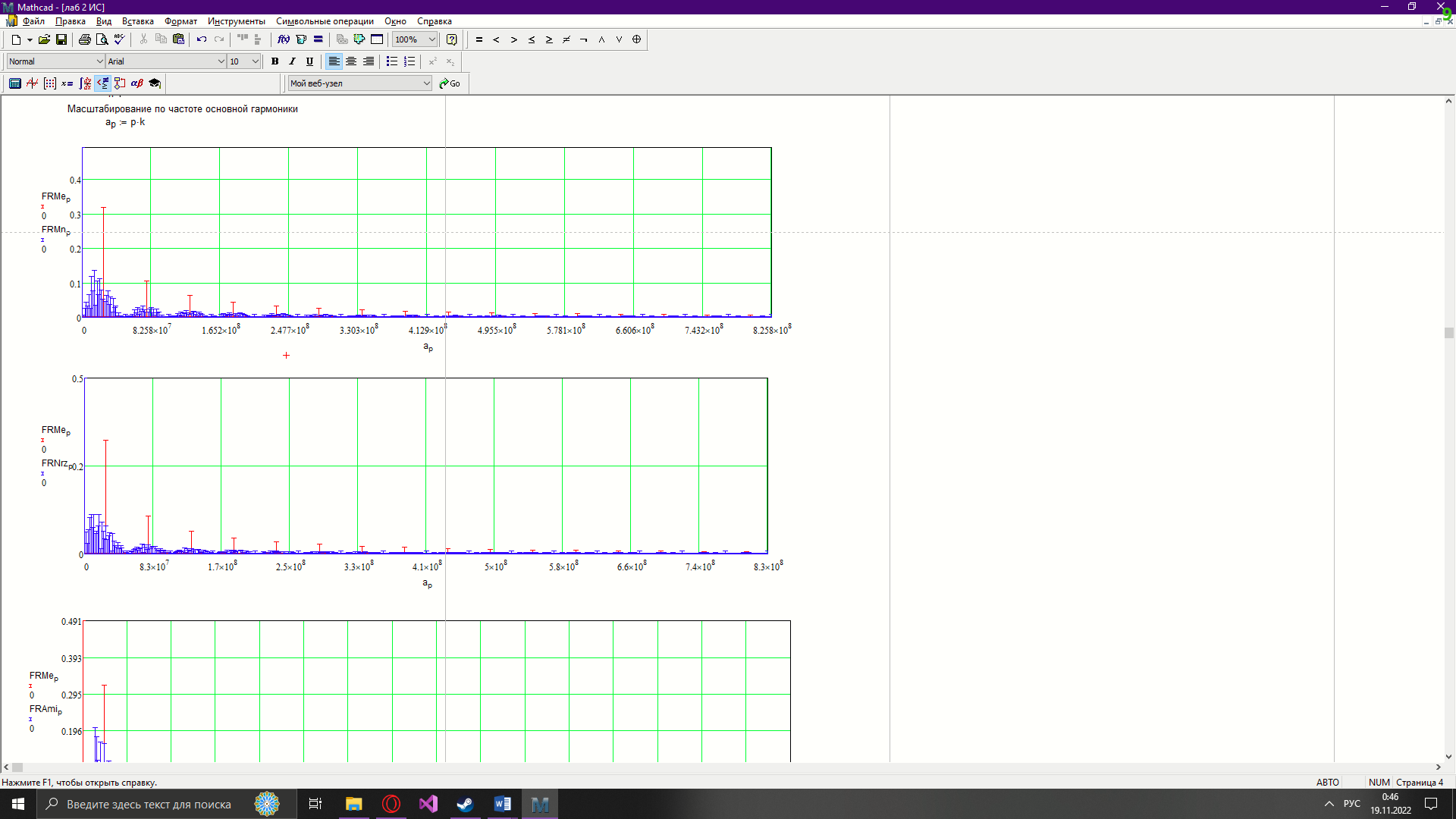 равнение спектров меандра и манчестерского равнение спектров меандра и манчестерскогоС 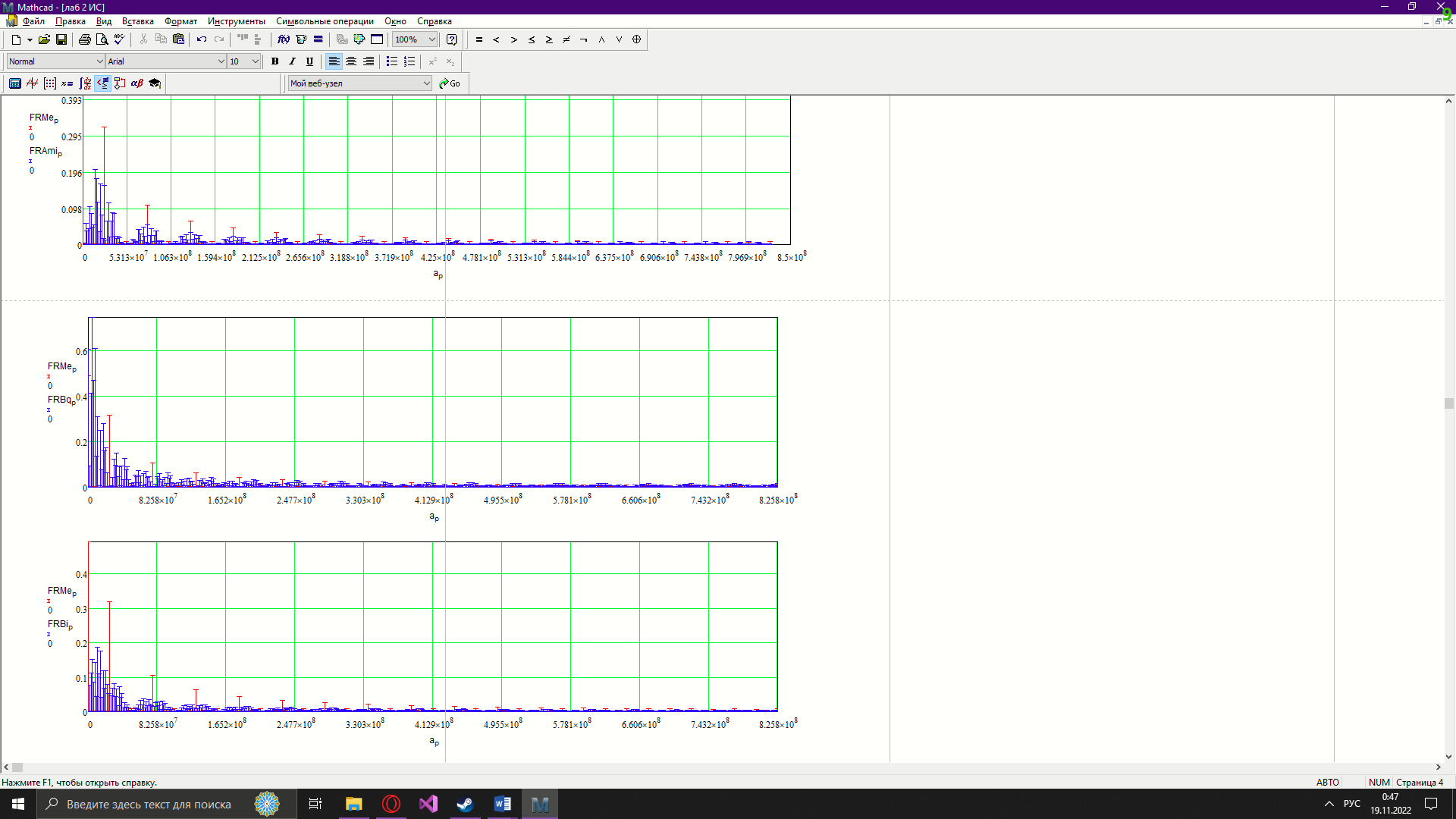 равнение спектров меандра и биполярного импульса равнение спектров меандра и биполярного импульсаС 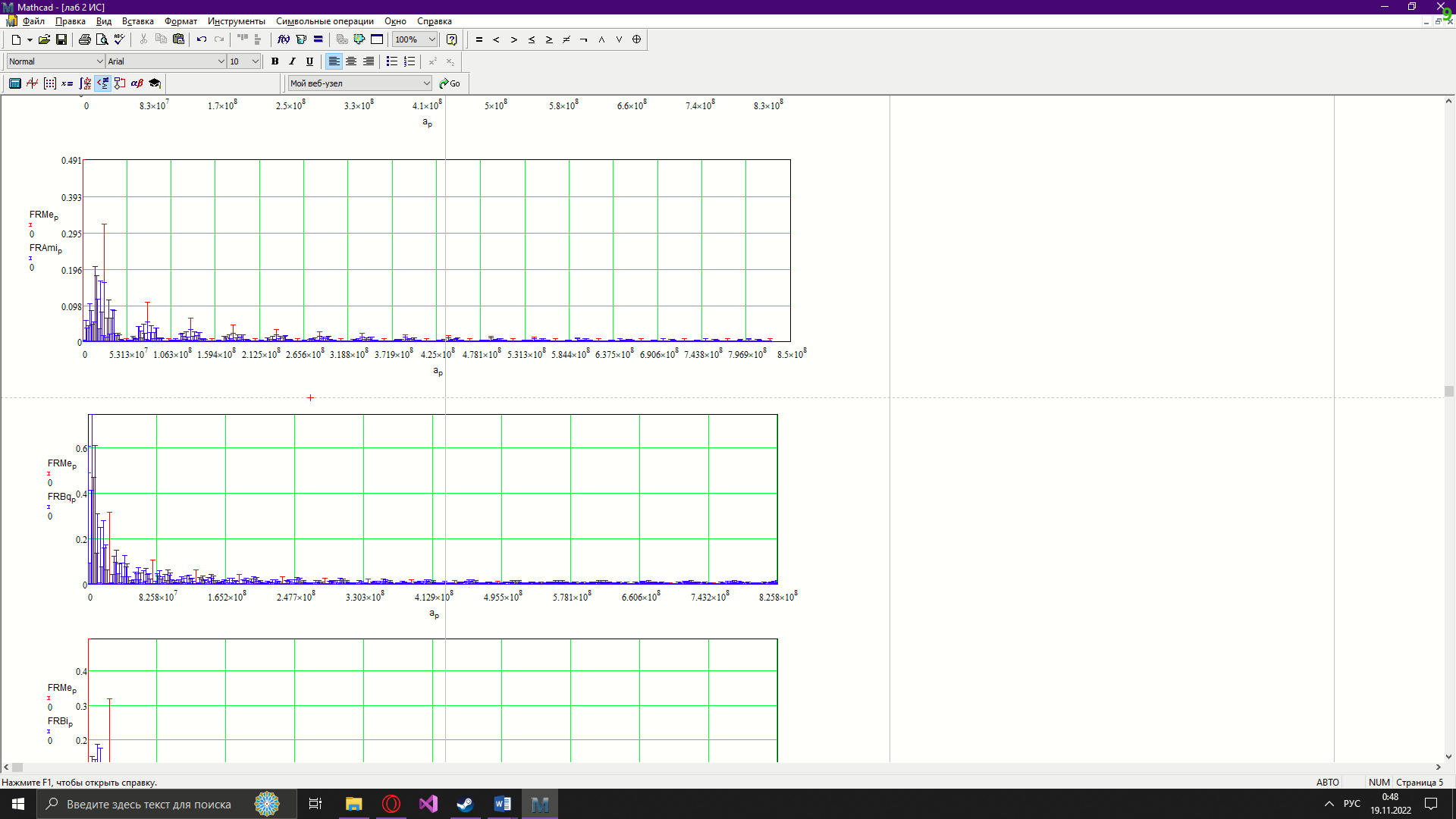 равнение спектров меандра и AMI равнение спектров меандра и AMIО 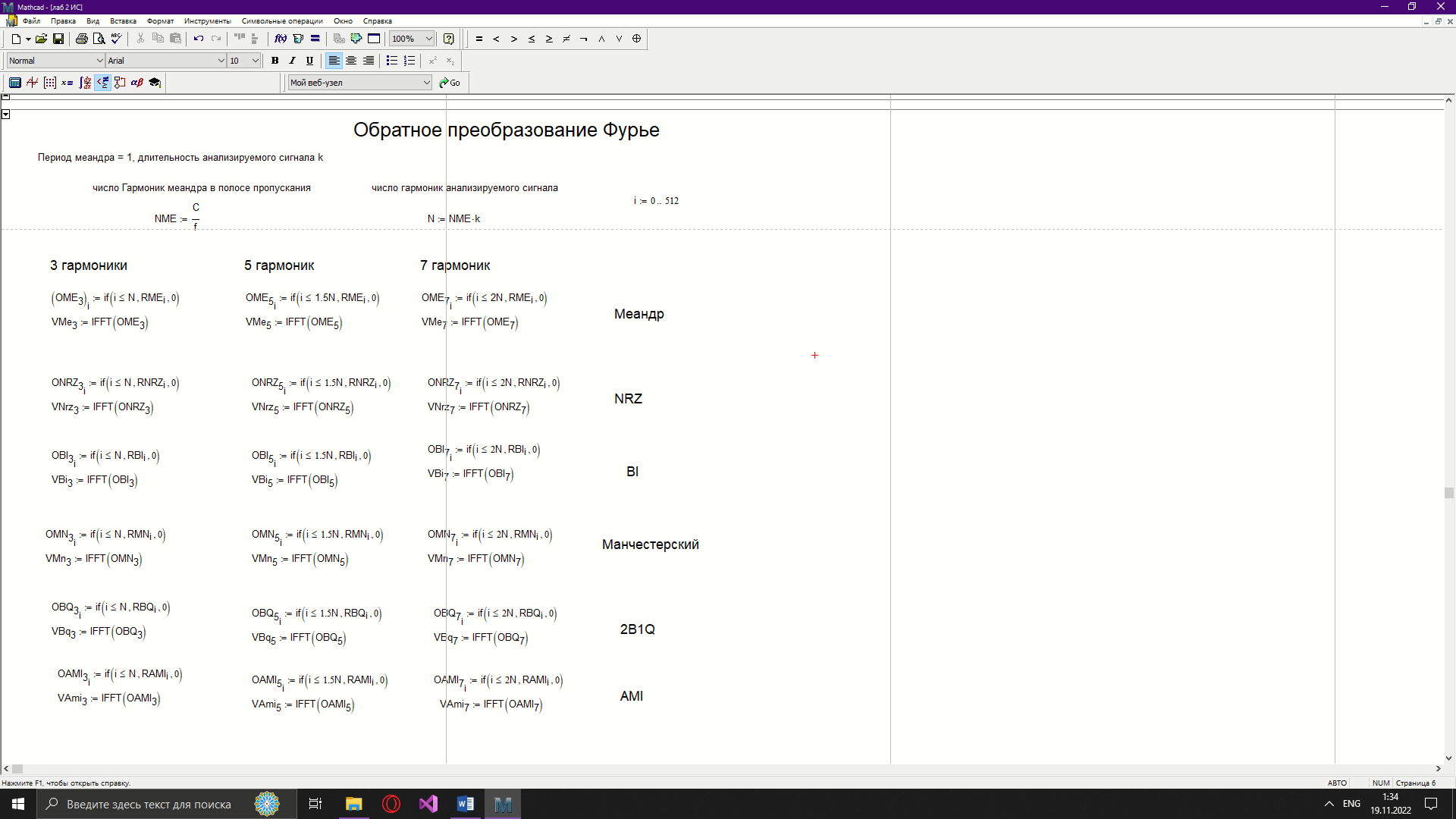 братное преобразование Фурье братное преобразование Фурье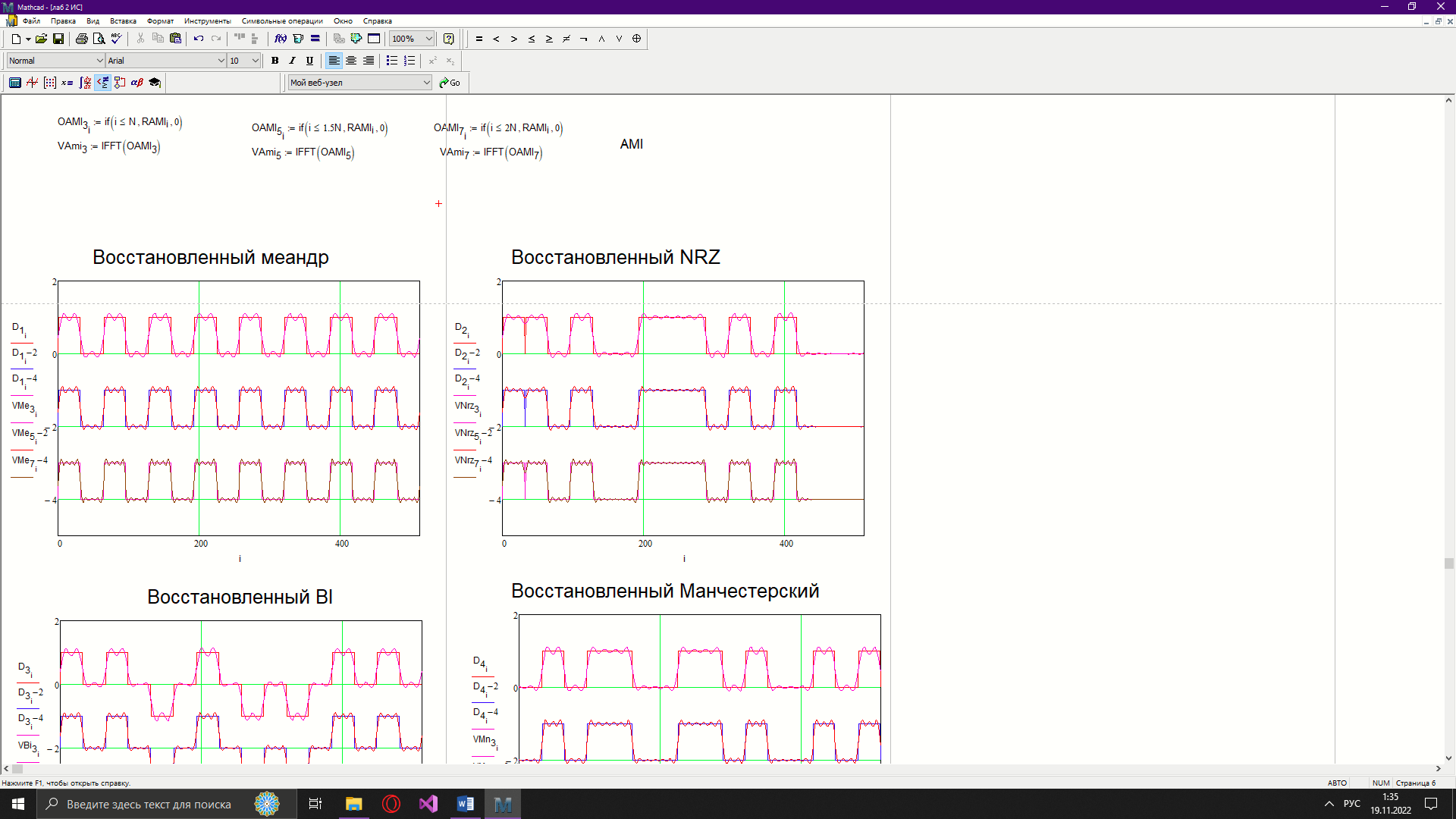  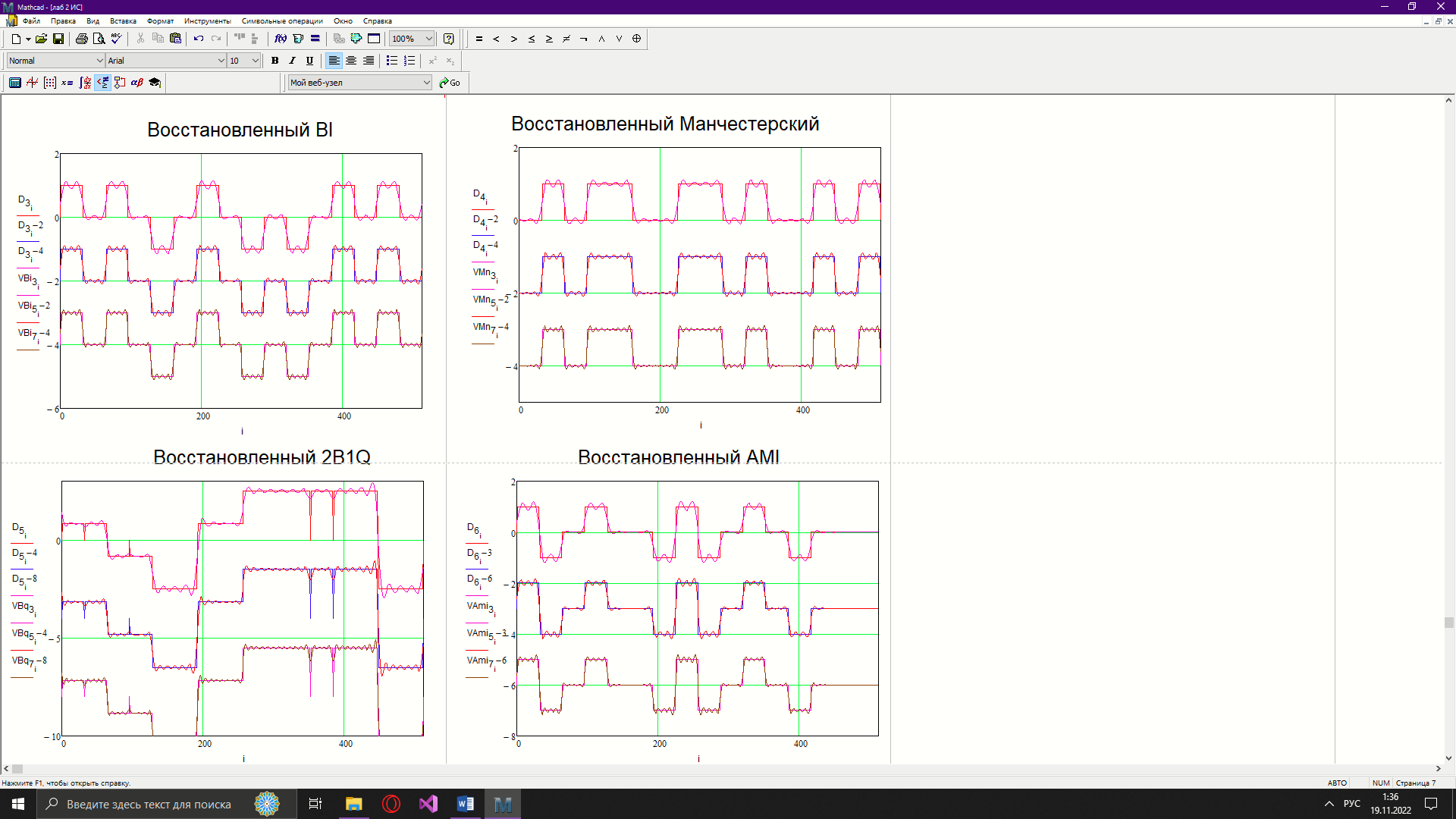    Определим погрешности в восстановленных сигналах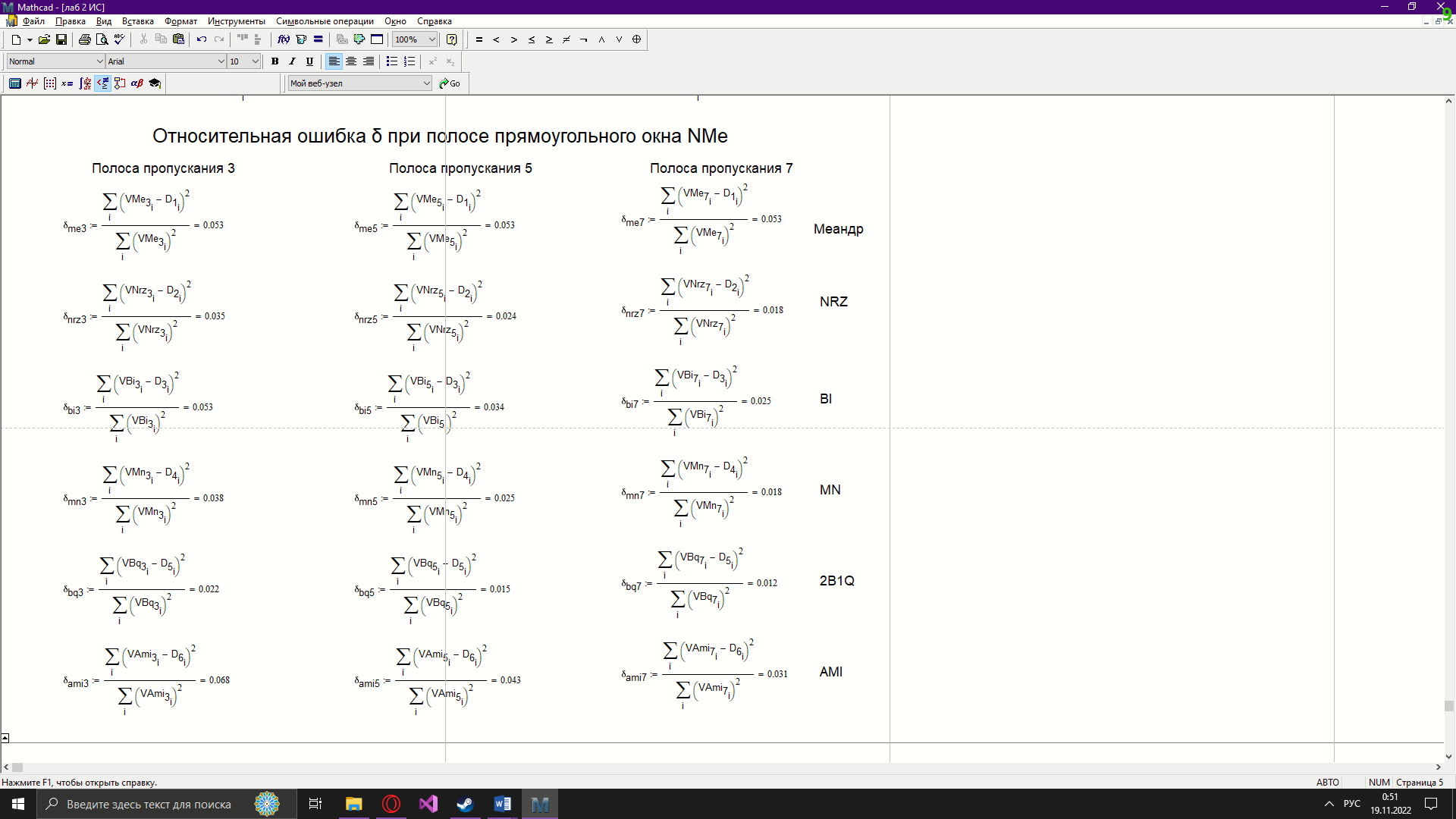 Таблица погрешностей при восстановлении сигналов
ЗаключениеВ рамках данной лабораторной работе из вектора значение NRZ были получены сигналы: 2B1Q, манчестерский, биполярный импульсный и AMI. Построены графики сигналов. С помощью функции FFT() инструмента Mathcad были получены спектры сигналов. Рассмотрены амплитудные спектры сигналов в сравнении с меандрическим сигналом. После ограничения количества спектральных составляющих, сигналы были восстановлены обратно во временную область. Восстановленные сигналы рассмотрены с оригиналами. Рассчитаны погрешности восстановления для разных условий ограничения (3, 5 и 7 гармоник). Установлено, что при большем количестве спектральных составляющих увеличивается точность восстановления (что следует из теории сигналов). В реальных средах передачи сигналов нет идеальных условий, поэтому все сигналы подвергаются искажению. Важно учитывать этот факт при проектировке и организации информационных сетей. | |||||||||||||||||||||||||||||||||||||||||
