Оптимальное управление быстродействием движущегося объекта с ограничениями на состояние. Оптимальное управление быстродействием движущегося объекта с огр. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования оренбургский государственный университет
 Скачать 293.94 Kb. Скачать 293.94 Kb.
|
|
Министерство образования и науки Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Математический факультет Кафедра прикладной математики и информатики КУРСОВАЯ РАБОТА по Теории оптимального управления Оптимальное управление быстродействием движущегося объекта с ограничениями на состояние ОГУ 010400.3015.031 ОО Оренбург 2015 Аннотация Рассматривается аналитический метод решения задачи оптимального быстродействия «В лодке с Понтрягиным» с фазовыми ограничениями и учетом ограниченности ресурсов системы. Содержание Введение 4 1 Постановка задачи 5 2 Классический пример Понтрягина и его лодка 7 Практическая часть 13 Заключение 15 Список использованных источников 16 ВведениеСоздание систем управления, обеспечивающих минимум времени переходного процесса с учетом требований на их динамические свойства, приводит к постановке задачи оптимального быстродействия с различного вида ограничениями. Основная задача состоит в определении таких граничных условий из заданных множеств и управлений из заданного функционального пространства, которые обеспечивают переход объекта управления из одного состояния в другое за минимально возможное время с учетом ограниченности ресурсов, зоны нормального функционирования системы и интегральных ограничений. Задача создания оптимальных по быстродействию систем возникает при разработке следящих систем, автоматических компенсаторов, систем управления приводами прокатных станов, ракетами, подъемными устройствами и систем автоматизации и других технических устройств. 1 Постановка задачиРассмотрим задачу быстродействия вида 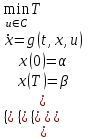 (1), (1),где 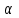 и и 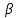 - фиксированные точки из пространства - фиксированные точки из пространства 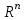 , , 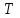 - время окончания, которое неотрицательно и свободно, - время окончания, которое неотрицательно и свободно, 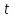 - время, - время, 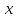 - траектория, - траектория, 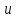 - управление, - управление, 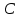 - множество допустимых управлений, - множество допустимых управлений, 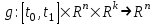 . .Следовательно, (1) является задачей перехода из состояния 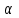 в состояние в состояние 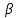 за минимальное время: такая задача называется оптимальной по быстродействию, ее решение имеет оптимальное время за минимальное время: такая задача называется оптимальной по быстродействию, ее решение имеет оптимальное время 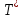 . . Так как 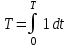 , Гамильтониан имеет вид , Гамильтониан имеет вид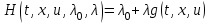 (2) (2)Сформулируем следующую теорему. Теорема 1. Рассмотрим задачу (1), в которой 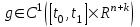 . Пусть . Пусть 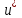 - оптимальное управление с временем окончания - оптимальное управление с временем окончания 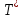 , а , а 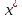 - соответствующая траектория. Тогда существует множитель - соответствующая траектория. Тогда существует множитель 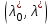 , где , где 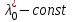 , , 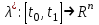 - непрерывна, - непрерывна, 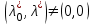 и ивыполняется принцип максимума Понтрягина 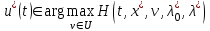 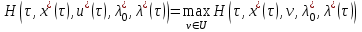 справедливы сопряженные уравнения 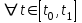 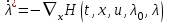 условия трансверсальности имеют вид 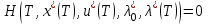 (3) (3)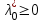 Так как задача оптимального быстродействия относится к задаче с переменным временем, то сложно сформулировать достаточные условия оптимальности. В следующем примере рассмотрим два различных подхода, гарантирующие, что экстремаль действительно является оптимальным решением. Пример 1. Рассмотрим 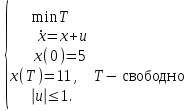 Гамильтониан имеет вид 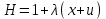 . .Необходимые условия оптимальности дают следующие результаты: Согласно принципу максимума Понтрягина 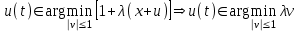 (4) (4)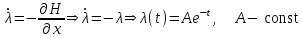 Из (3), для некоторой константы 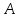 , имеем , имеем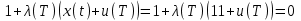 (5) (5)Легко видеть, что 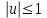 и (5) получаем и (5) получаем 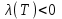 , то есть , то есть 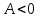 . Значит из (4) имеем . Значит из (4) имеем 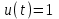 на на 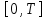 . Уравнение динамики . Уравнение динамики 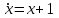 с начальным условием с начальным условием 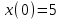 дает решение дает решение 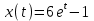 . .Используя конечное условие 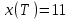 , получим значение , получим значение 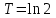 . .Вернемся к условию (5): 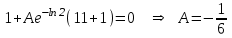 . .2 Классический пример Понтрягина и его лодкаПредположим, что мы находимся на лодке, которая в момент времени 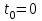 имеет расстояние имеет расстояние 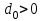 от причала пирса и скорость от причала пирса и скорость 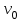 в направлении пирса. Лодка оснащена мотором, который обеспечивает ускорение или замедление. Мы ищем стратегию, чтобы прибыть к пирсу в кратчайшие сроки с «мягкой стыковкой», т. е. с нулевой скоростью в финальный момент времени в направлении пирса. Лодка оснащена мотором, который обеспечивает ускорение или замедление. Мы ищем стратегию, чтобы прибыть к пирсу в кратчайшие сроки с «мягкой стыковкой», т. е. с нулевой скоростью в финальный момент времени 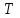 . .Введем обозначения 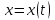 - расстояние от причала в момент времени - расстояние от причала в момент времени 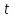 , ,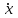 – скорость лодки – скорость лодки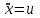 – ускорение ( – ускорение (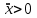 ) или замедление ( ) или замедление (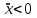 ) )Для того чтобы получить «мягкую стыковку», мы потребуем 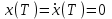 , где , где 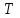 – конечное время (явно неизвестно). – конечное время (явно неизвестно).Отметим, что наша стратегия зависит только от нашего выбора в каждый момент времени 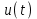 . .Получаем задачу оптимального управления: 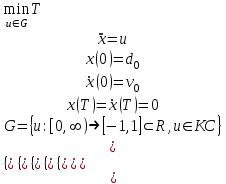 (6) (6)где 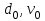 - фиксированы, - фиксированы, 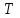 - свободно (неизвестно). - свободно (неизвестно).Модель (6) – один из возможных вариантов представления данного классического примера. Рассмотрим задачу (6) «В лодке с Понтрягиным», положим 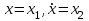 и получим и получим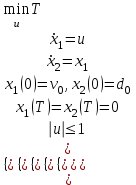 (7), (7),где 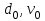 - фиксированные константы, - фиксированные константы, 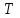 - положительно. - положительно.Гамильтониан 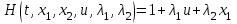 и необходимые условия теоремы 1 дают и необходимые условия теоремы 1 дают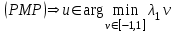 (8) (8)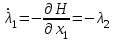 (9) (9)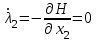 (10) (10)(7) 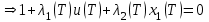 (11) (11)Простые вычисления из (9) и (10) дают 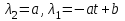 (12), (12),где 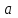 и и 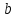 - константы. - константы.Из (PMP) в (8) мы имеем 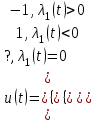 Предположим, что на всем интервале 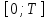 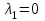 , то мы получим , то мы получим 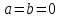 . По (12) . По (12)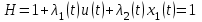 : :Но данный результат противоречит (11), следовательно, ситуация с 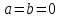 невозможна. Значит, невозможна. Значит, 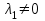 и является прямой линией, тогда существует не более одной точки переключения и является прямой линией, тогда существует не более одной точки переключения 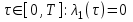 , в которой управление , в которой управление 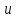 имеет разрыв первого рода (скачок). имеет разрыв первого рода (скачок). Рассмотрим два случая. Случай А. Допустим 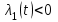 для для 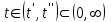 . Тогда для любого . Тогда для любого 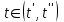 имеем имеем 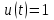 , а значит , а значит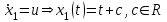 (13) (13)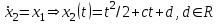 (14) (14)Преобразуем (14) к виду 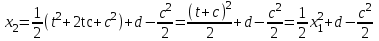 (15) (15)На данный момент не так то просто найти константы 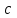 и и 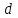 : однако ясно, что (15) представляет некоторые параболы на плоскости : однако ясно, что (15) представляет некоторые параболы на плоскости 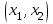 . Кроме того, уравнение динамики . Кроме того, уравнение динамики 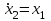 дает, что если дает, что если 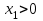 , то функция , то функция 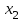 возрастает и если возрастает и если 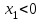 , то , то 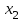 убывает (на рисунке 1 указаны соответствующие направления). убывает (на рисунке 1 указаны соответствующие направления).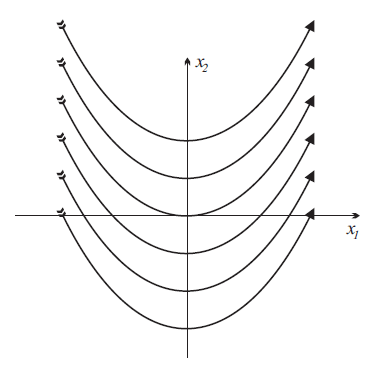 Рисунок 1. Случай В. Допустим 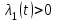 при при 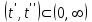 . Тогда для любого . Тогда для любого 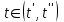 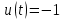 , а значит , а значит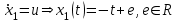 (16) (16)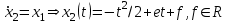 (17) (17)Аналогично предыдущему случаю, получаем 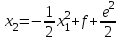 (18) (18)Снова у нас есть некоторый набор парабол с указанным направлением движения. 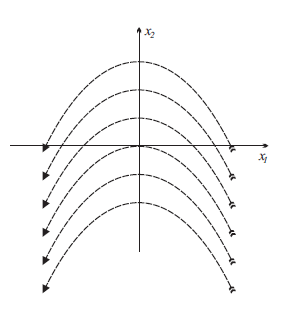 Рисунок 2. Случай А+В. Теперь соединим вместе эти два семейства парабол в (15) и (17) (рисунок 3). 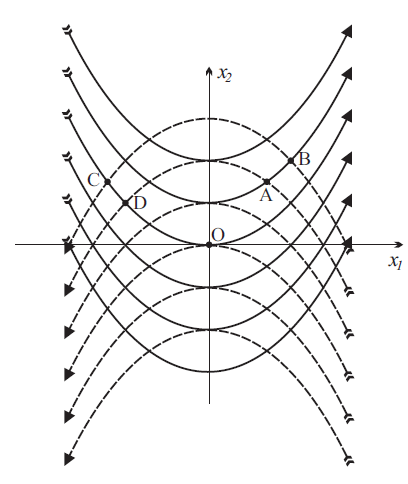 Рисунок 3. Для того чтобы в начальный момент времени 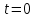 стартовав из точки стартовав из точки 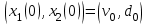 , прибыть в момент окончания времени , прибыть в момент окончания времени 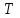 в точку в точку 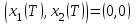 , мы можем проследить вдоль различных участков таких парабол (с верным направлением). Понятно, что существует бесконечное множество таких путей: например, начиная из точки , мы можем проследить вдоль различных участков таких парабол (с верным направлением). Понятно, что существует бесконечное множество таких путей: например, начиная из точки 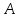 мы можем двигаться по кривой, прибыв в точку мы можем двигаться по кривой, прибыв в точку 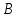 , затем следуя по пунктирной линии, прибыть в точку , затем следуя по пунктирной линии, прибыть в точку 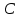 и попасть в начало новой параболы. и попасть в начало новой параболы.Заметим, что каждый раз, когда мы переходим от одной кривой на другую, оптимальное управление имеет точку разрыва, т.е. 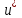 проходит от +1 до -1 и наоборот. Поскольку мы знаем, что оптимальное управление имеет не более одной точки разрыва, то «красная линия ADO» - это единственная прямая, чтобы показать минимальный путь. проходит от +1 до -1 и наоборот. Поскольку мы знаем, что оптимальное управление имеет не более одной точки разрыва, то «красная линия ADO» - это единственная прямая, чтобы показать минимальный путь.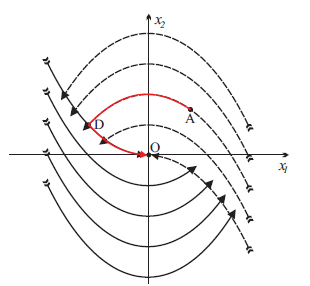 Рисунок 4. Практическая частьРассмотрим задачу 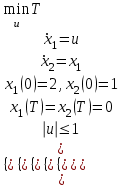 Поскольку 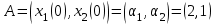 , по (16) и (17) мы получаем , по (16) и (17) мы получаем 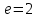 и и 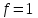 . Условие (15) дает кривую . Условие (15) дает кривую 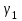 с уравнением с уравнением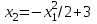 . .Точка 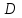 является точкой пересечения кривой является точкой пересечения кривой 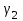 , заданной уравнением , заданной уравнением 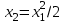 , и кривой , и кривой 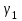 : мы получаем : мы получаем 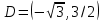 . Отметим, что начиная с . Отметим, что начиная с 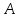 в момент времени в момент времени 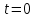 , мы приходим в точку , мы приходим в точку 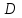 в момент времени в момент времени 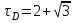 по (16). по (16).Начиная от точки 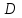 , прибываем, по кривой , прибываем, по кривой 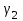 , к точке , к точке 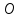 . . Из условия (13) получаем 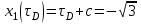 ⇒ ⇒ 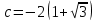 . . Из условия (15) и уравнения 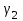 , мы имеем , мы имеем 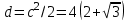 . . В момент времени 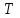 мы приходим в начало координат, используя (13), получим мы приходим в начало координат, используя (13), получим 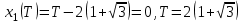 . . Следовательно 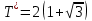 . .Оптимальное управление и оптимальные траектории окончательно примут вид (графики оптимальных решений представлены на рисунке 5) 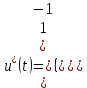 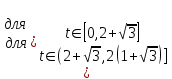 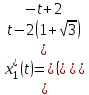 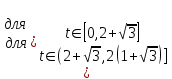 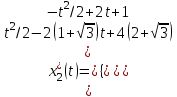 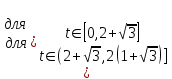 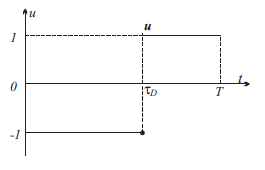 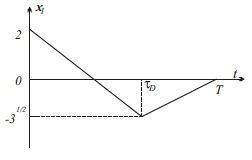 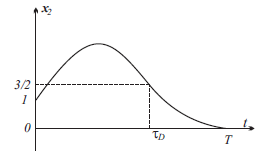 Рисунок 5 – Оптимальное решение задачи. ЗаключениеЗадачи оптимального управления встречаются на практике (например, при описании импульсных систем) и потому представляют интерес не только как конечноразностные аналоги непрерывных задач. Задачи оптимизации управляемых процессов, или как они будут в дальнейшем называться, задачи оптимального управления, составляют один из широких классов экстремальных задач и имеют важное прикладное значение. Структурная схема задачи управления состоит из двух звеньев: управляющего органа и объекта управления. В качестве объекта управления может служить, например, космический эксперимент, экономика отрасли промышленности, система машин, семейный бюджет и т. д. Управляющее звено со времени возникновения задач управления претерпело эволюции от простейшего регулятора до современной ЭВМ. Список использованных источниковCalogero, А. Notes on optimal control theory with economic models and exercises/ A. Calogero // Dipartimento di Matematica e Applicazioni. - 2014. Айсагалиев, С.А. Дифференциальные уравнения и процессы управления / С.А. Айсагалиев // Оптимальное управление. – 2010. |
