Федеральное государственное образовательное ордена трудового красного знамени бюджетное учреждение высшего профессионального
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ (МТУСИ) Кафедра информатики Лабораторная работа № 1 «Методы решения нелинейных уравнений» Почему все-таки берете х0 =1.? Ведь это условие f(1) * f´´(x) > 0 в т. 1 не выполняется нигде, т.к. 2 производная везде отрицательная. Но метод все равно сходится. Объясните Точка 1 выбрана, т.к. находится в промежутке [1; 2], где f(1)*f``(1) < 0 и f(2)*f``(2) > 0. В отчёте была допущена опечатка, границы были 0 и 1 соответственно. Выполнил студент группы “Сортирный Союз” username Москва 2021 Индивидуальное задание
Протокол вычислений Отделение корней   format(8); disp(p); 1. 0.38602 -0.70969 -0.58733 1.2 0.24073 -0.74308 -0.69942 1.4 0.08886 -0.77545 -0.74921 1.6 -0.0694 -0.8071 -0.78992 1.8 -0.23395 -0.83824 -0.82642 2. -0.40468 -0.86901 -0.86053 function s = fi(x) deff('y = f(x)', 'y = cos(x / 5) * (1 + x)^(0.5) - x'); plot([1 : 0.2 : 2], f); xtitle('', 'x', 'f(x)') xgrid; dy = numderivative(f, x); dy2 = numderivative(f, x, 2); s = [x, f(x), dy, dy2]; endfunction p = zeros(6, 4); x = 1 : 0.2 : 2; for i = 1 : 6 p(i, :) = fi(x(i)); end 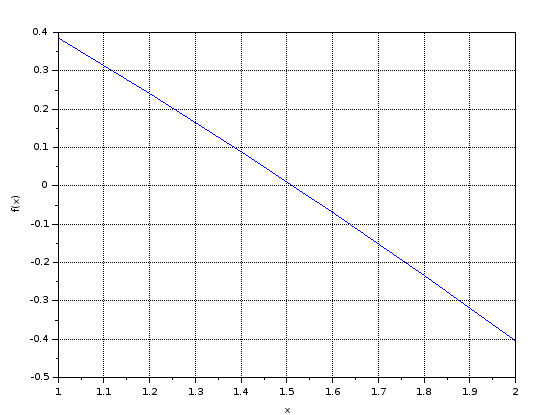 Вывод: на концах отрезка [1; 2] функция имеет противоположные знаки, 1-я производная знакопостоянна - значит, на этом отрезке уравнение имеет единственный корень Уточнение корней методом половинного деления  function fbs = f(x) //lab_1_1.sci fbs = cos(x / 5) * (1 + x)^(0.5) - x; endfunction disp(' n a b f(a) f(b) c=(a+b)/2 f(c) b-a'); n = 0; fa = f(a); fb = f(b); c = (a + b) / 2; fc = f(c); z = [n, a, b, fa, fb, c, fc, b - a]; disp(z); for n = 1 : 3 if f(c) * f(a) < 0 then b = c; else a = c; end fa = f(a); fb = f(b); c = (a + b) / 2; fc = f(c); z = [n, a, b, fa, fb, c, fc, b - a]; disp(z); c = (a + b) / 2; end На отрезке [1; 2] условие сходимости для функции выполняется; начальным приближением x0 является точка 1,5  a = 1; b = 2; exec('/home/peppermint/Documents/study/chislometh/lab_1_1.sci'); " n a b f(a) f(b) c=(a+b)/2 f(c) b-a" 0. 1. 2. 0.38602 -0.40468 1.5 0.01052 1. 1. 1.5 2. 0.01052 -0.40468 1.75 -0.19223 0.5 2. 1.5 1.75 0.01052 -0.19223 1.625 -0.08963 0.25 3. 1.5 1.625 0.01052 -0.08963 1.5625 -0.03925 0.125
После трёх итераций приближение к корню x3 = 1.525 Погрешность результата: |b3 - a3| = 0.125 Уточнение корней методом Ньютона Из условия, где f(1) * f´´(1) < 0 и f(2) * f´´(2) > 0 выберем начальное приближение к корню x0 = 1. Функция и 2 производная имеют разные знаки в т. х=1????? Для получения решения методом Ньютона воспользуемся рекуррентной формулой xn+1=xn-f(xn)/f´(xn).  #include "iostream" #include "cmath" using namespace std; double func_orig(double x) { return cos(x / 5) * pow(1 + x, 0.5) - x; } double func_der(double x) { return -((sqrt(x + 1) * sin(x / 5)) / 5) - 1 + (cos(x / 5) / (2 * sqrt(x + 1))); } int main() { int n = 0; double x_curr = 0.5, x_last = 1; cout << "n x f(x) f'(x)" << endl; while (abs(x_last - x_curr) > 1E-4) { x_last = x_curr; n++; x_curr = x_last - (func_orig(x_last) / func_der(x_last)); cout << n << " " << x_curr << " " << func_orig(x_curr) << " " << func_der(x_curr) << endl; } return 0; } НЕВЕРНО! Программируемый метод делается до заданной точности!!!!!! Исправить!
Решение уравнения функцией fsolve()  deff('y = g(x)', 'y = cos(x / 5) * (1 + x)^(0.5) - x'); fx = fsolve(0, g) fx = 1.51328 Скриншоты: 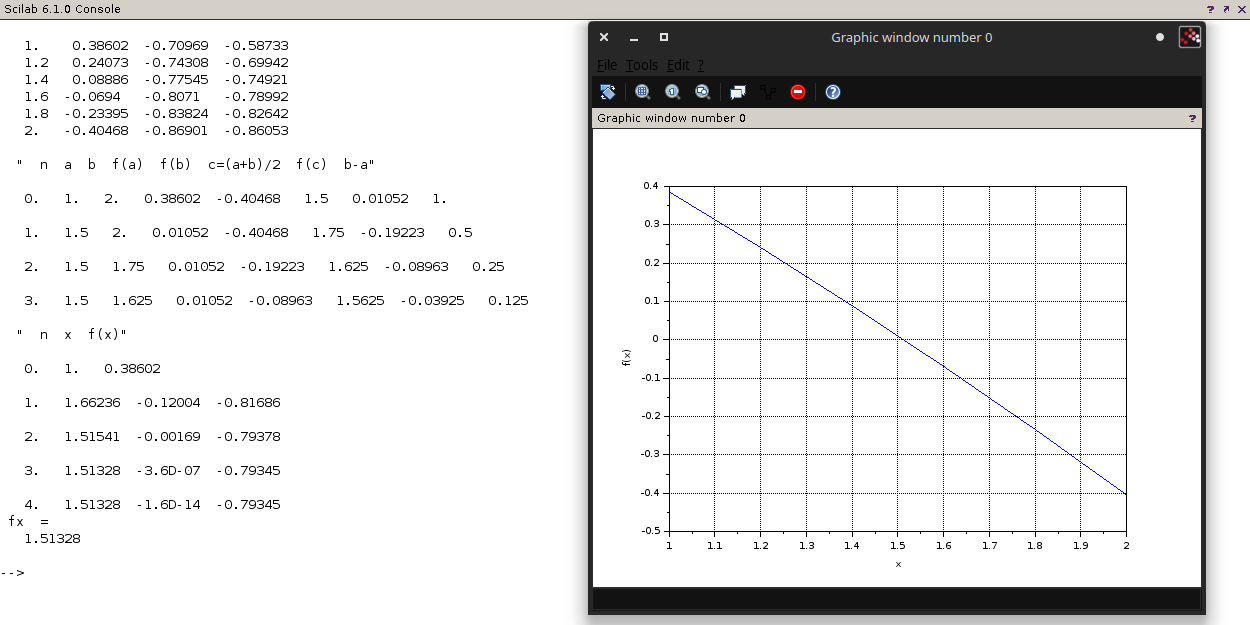 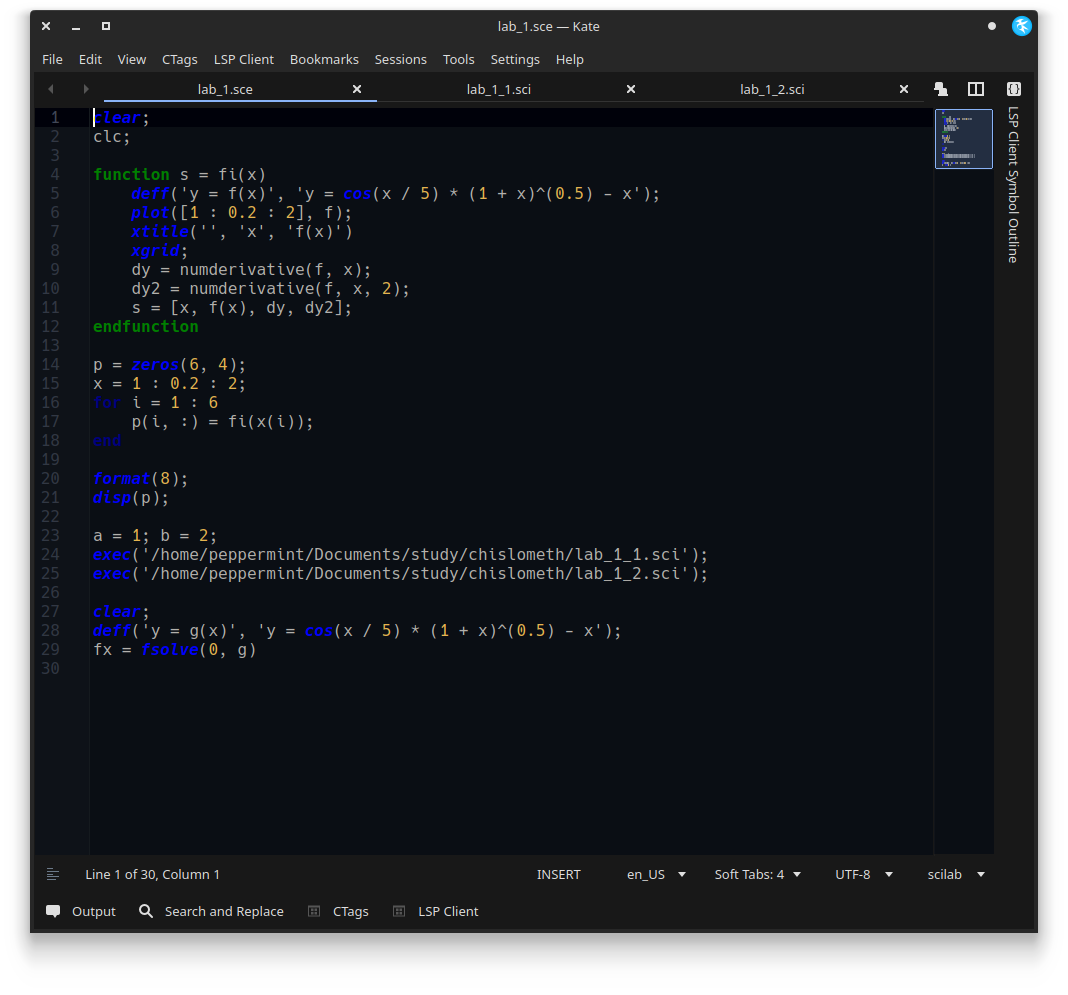 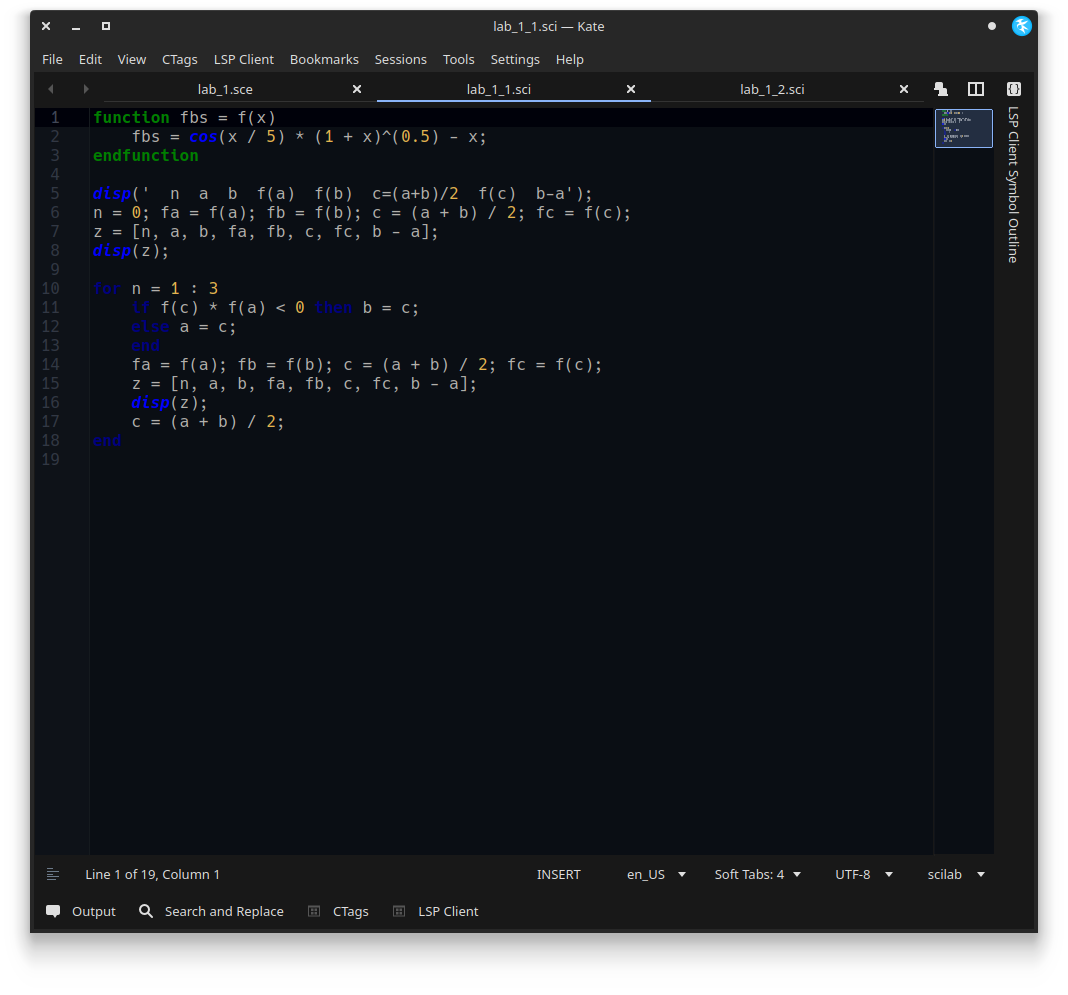 ВЫ изучали ? СИ++. Вот в этой среде и надо программировать!!! Нет, не изучал, но читал достаточное количество кода на данном языке программирования. На первом курсе обучение программированию проходило на VB.Net, а в методичке (и в лекциях) ни слова не сказано про использование конкретного «средства программирования». Как я понимаю, писать можно на чём угодно, но специально по вашей просьбе мною была написана реализация на C++. Схему алгоритма я давал на лекции. Вот ее и используйте. 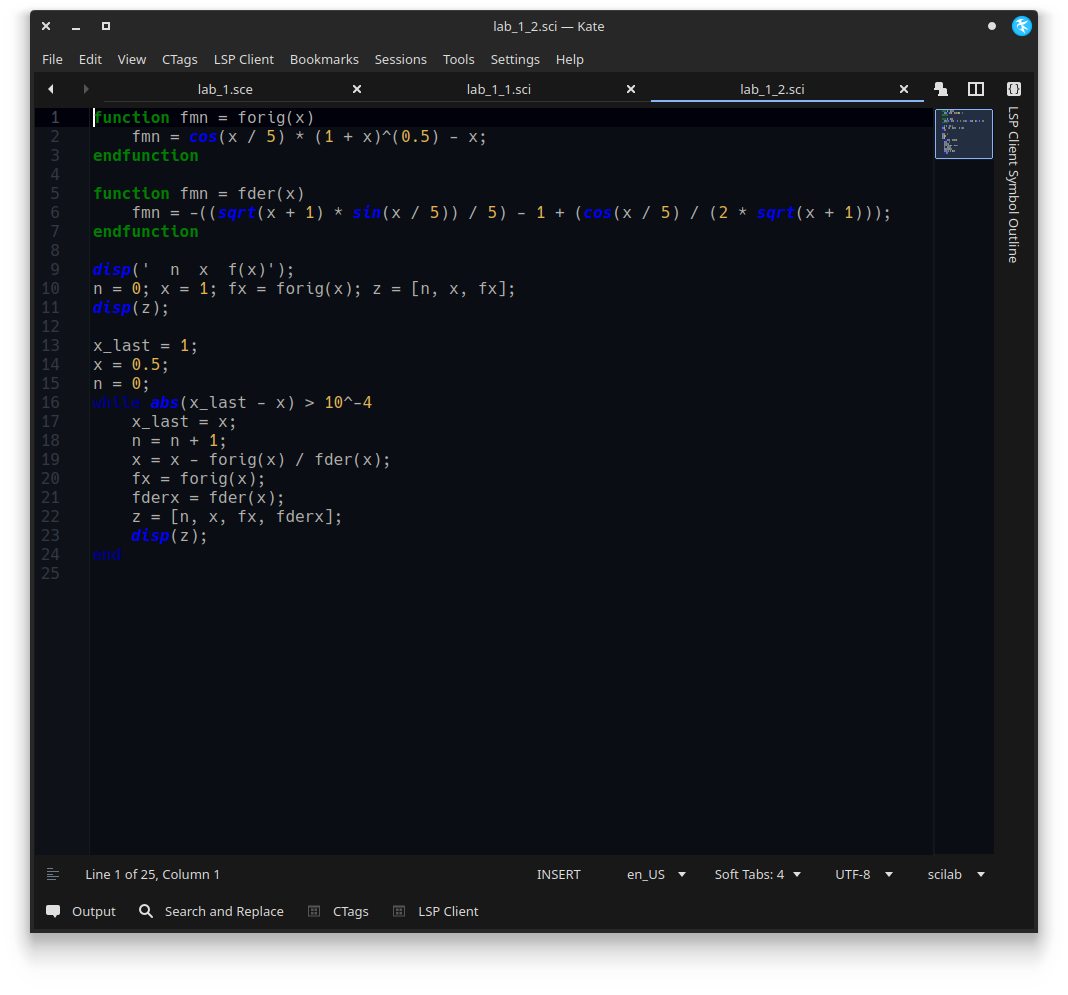 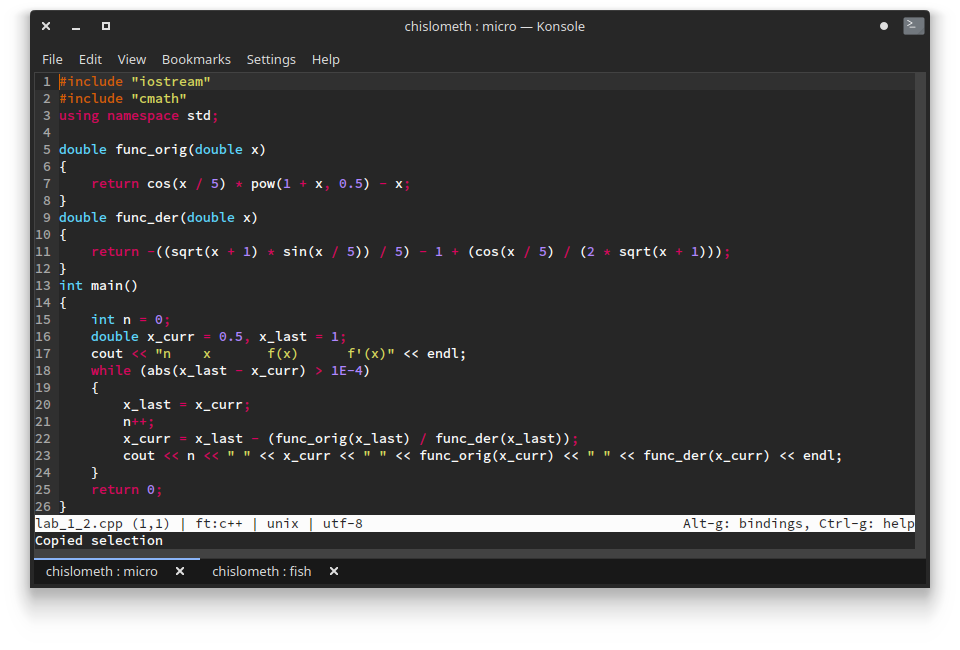 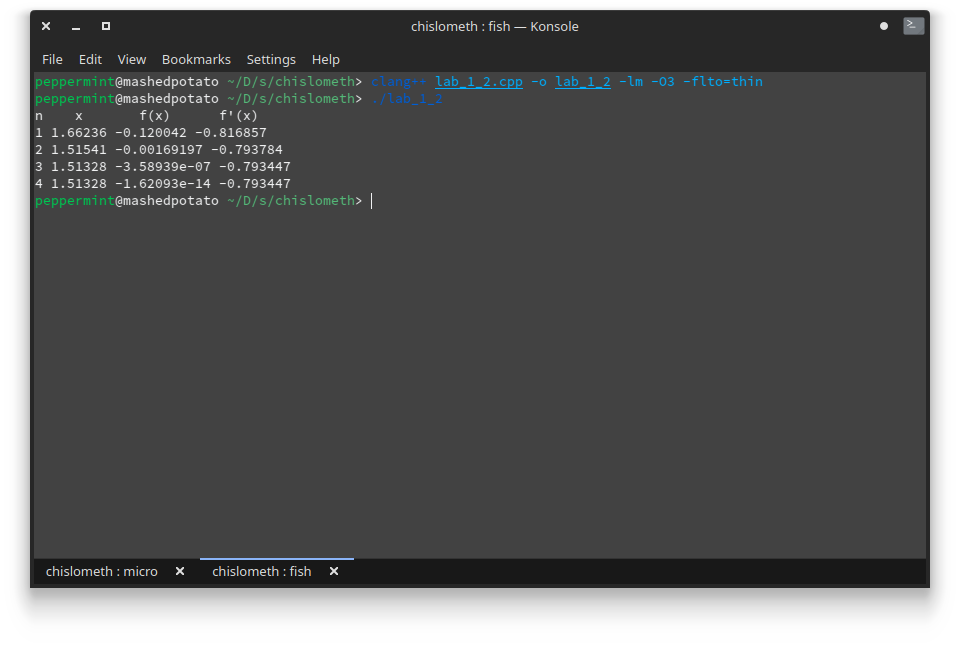 |
