РГР 1. Филиал фгбоу во угнту в г. Салавате

• Название: Филиал фгбоу во угнту в г. Салавате
• Дата: 15.05.2023
• Размер: 317.5 Kb.
• Имя файла: РГР 1.doc
• Тип: Документы; #1132260

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный нефтяной технический университет» (ФГБОУ ВО УГНТУ)

Филиал ФГБОУ ВО УГНТУ в г. Салавате
Кафедра «Информационных технологий»


Физика


Расчетно-Графическая работа

классическая механика

Ин.Тех.-09.03.01-1.01.05 РГР


Исполнитель:

студент гр. БАБз-21-21 Е.А. Витальев

Руководитель:

ассистент Г.Ф. Шаяхметов

Салават
2022

расчетное задание № 1

Классическая механика

1.5 Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью V₁ = 18 км/ч. Далее половину оставшегося времени он ехал со скоростью V₂ = 22 км/ч, после чего до конечного пункта он шел пешком со скоростью V₃ = 5 км/ч. Определить среднюю скорость < V > велосипедиста .

Дано:



Найти:

Решение: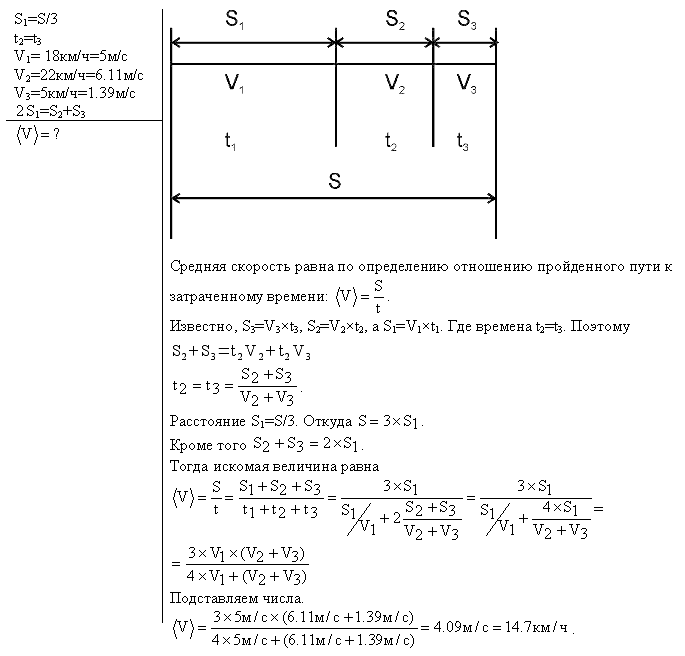



Средняя скорость равна по определению отношению пройденного пути к затраченному времени:
(1)
Известн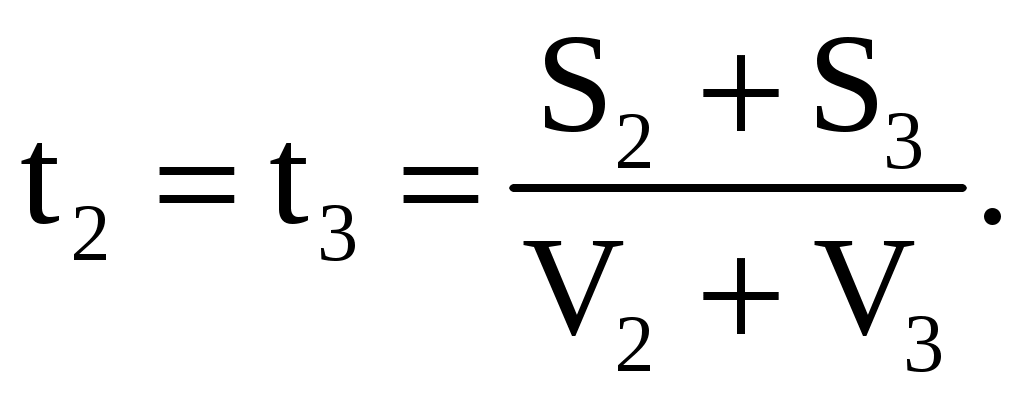о,
(2)
(3)

Расстояние
(4)
Откуда
(5)
Кроме того
(6)
Тогда искомая величина равна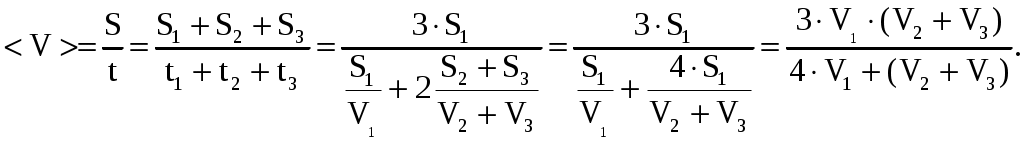
(7)
Подставляем числа.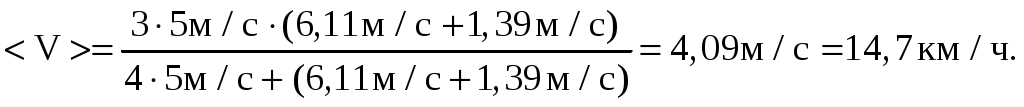



Ответ:

1.15 Конькобежец, стоя на коньках на льду, бросает камень массой т₁ = 2,5кг под углом, а = 30° к горизонту со скоростью v =10м/с. Какова будет начальная скорость v₀ движения конькобежца, если масса его m₂ = 60кг? Перемещением конькобежца вовремя броска пренебречь.

Дано:

Найти: V₂=?

Решение: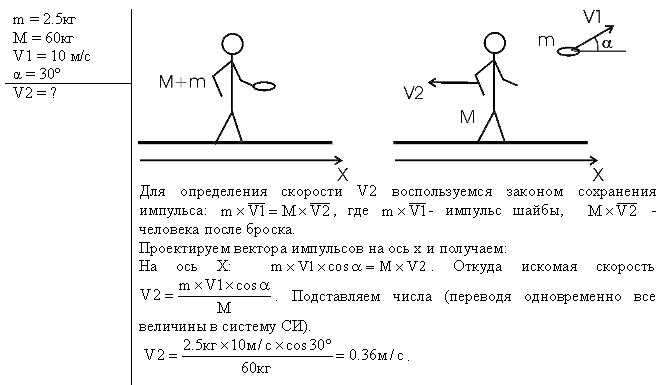


Для определения скорости V₂ воспользуемся законом сохранения импульса:
(8)
где - импульс шайбы;

- человека после броска.

Проектируем вектора импульсов на ось x и получаем:

На ось Х:
(9)
Откуда искомая скорость
(10)
Подставляем числа (переводя одновременно все величины в систему СИ).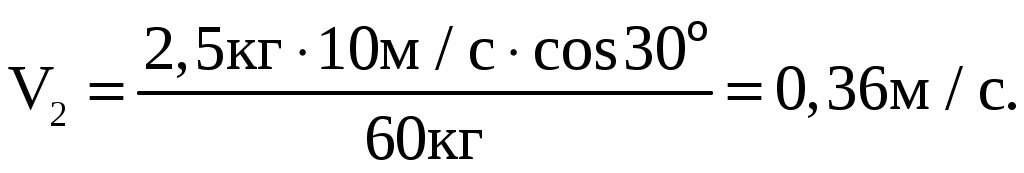

Ответ:
1.25 Определить КПД  неупругого удара бойка массой m₁ = 0,5т, падающего на сваю массой m₂ = 120кг. Полезной считать энергию, затраченную на вбивание сваи.

Дано:

Найти:

Решение:

Удар неупругий, поэтому происходит слипание тел и в дальнейшем (после удара) они двигаются вместе.

До удара кинетическая энергия бойка равна
(11)
а сваи
(12)
так как она не двигалась.

Их кинетическая энергия после взаимодействия:
(13)
где - общая скорость.
Используем закон сохранения импульса:
(14)
Откуда
(15)
Подставляем эту скорость в кинетическую энергию после взаимодействия: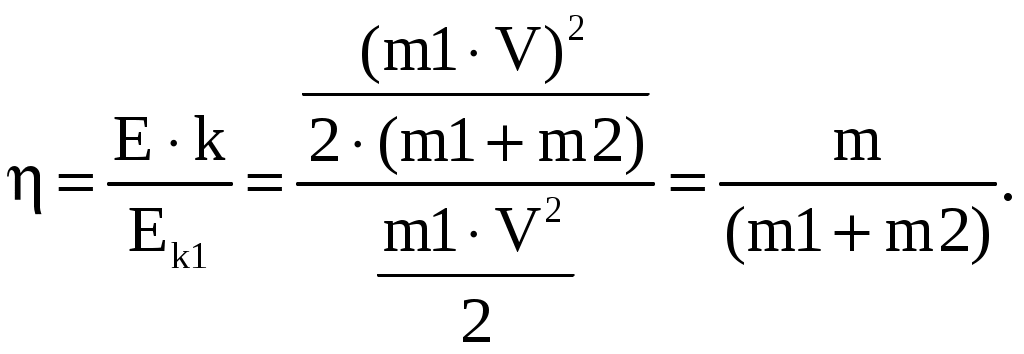
(16)
Подставляем числа: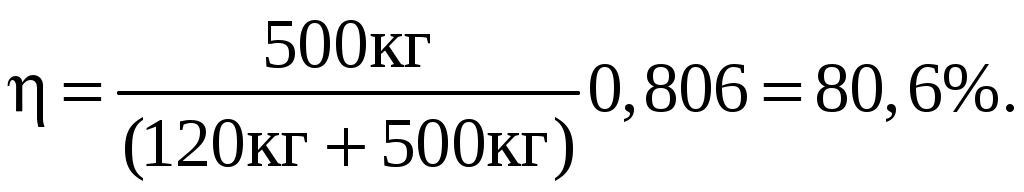

Ответ:
1.35) Какую нужно совершить работ А, чтобы пружину жесткостью k = 800Н/м, сжатую на х = 6см, дополнительно сжать на x = 8см?

Дано: k=800 H/м, x1=6см;

Найти:

Решение: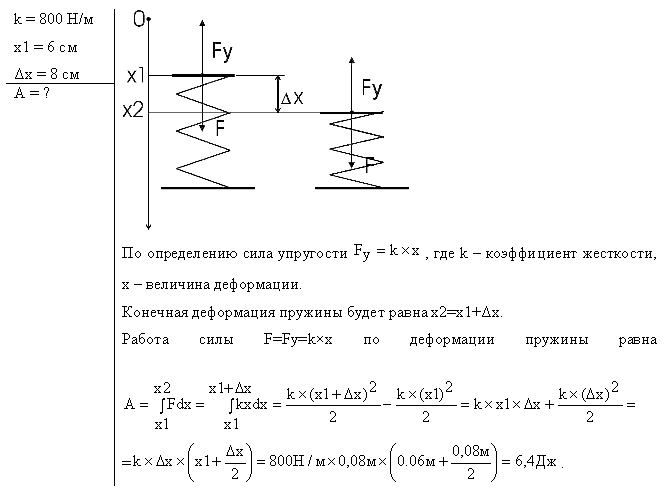



По определению сила упругости
, (17)
где k – коэффициент жесткости;

x – величина деформации.

Конечная деформация пружины будет равна
(18)
Работа силы
(19)
по деформации пружины равна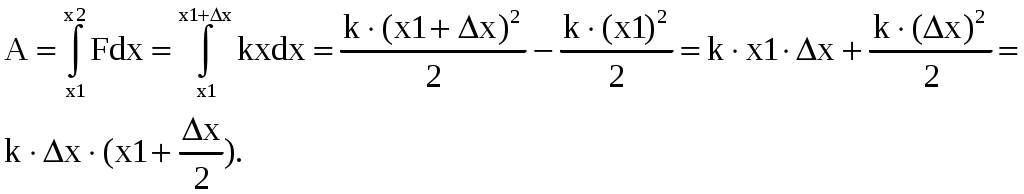
(20)


Ответ:

1.45) Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению  = At + Bt³ , где А = 2рад/с, В = 0,2рад/с³. Определить вращающий момент M, действующий на стержень через время t = 2с после начала вращения, если момент инерции стержня J =0.048 кг- м².

Дано:

Найти: М=?

Решение:

Из второго закона Ньютона, применяемого к вращающимся телам, находим
, (21)
где М- вращающий момент, - угловое ускорение, J- момент инерции диска.

По определению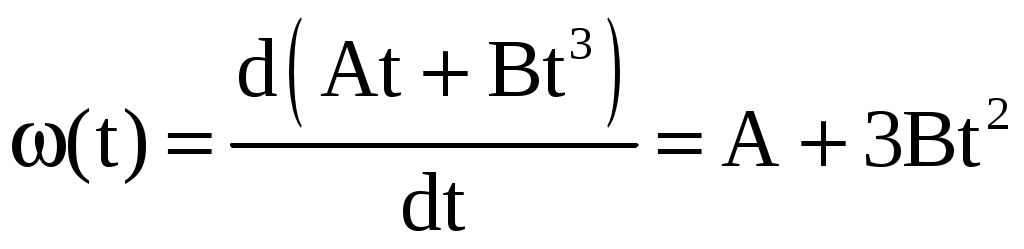
, (22)
; (23)
тогда (24)
По определению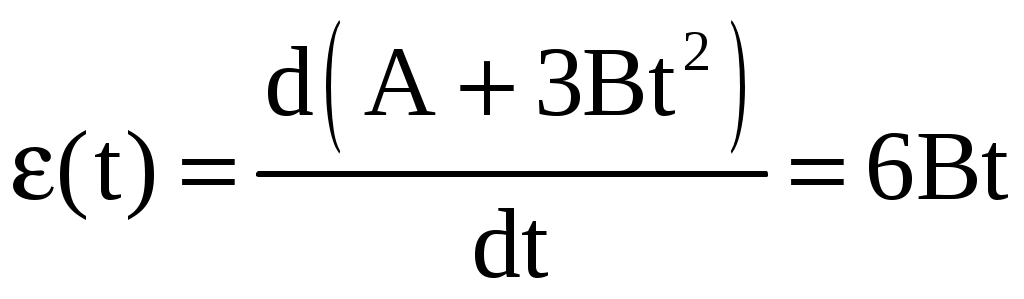
, (25)
тогда
(26)
В момент времени t=T

Тогда

Ответ: М=
1.55 Нa скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью W₁ = 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью w; станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол  = 90°? Момент инерции человека и скамьи J равен
2,5 кг∙м², момент инерции колеса J₀ = 0,5 кг-м².

Дано:

Найти:

Решение:


Из закона сохранения момента импульса имеем: в изолированной системе сумма моментов импульса всех тел- величина постоянная. Так как диск повернули на угол , то проекция его момента импульса на ось равна нулю, поэтому
, (27)
где J0- момент инерции диска;

J- момент инерции скамьи с человеком относительно оси .

Поэтому искомая величина

(28)
Ответ:
1.65 По круговой орбите вокруг Земли обращается спутник с периодом
Т = 90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

Дано:

Найти: r=?

Решение:



На всякое тело, движущееся по круговой орбите, действует центростремительная сила (если мы поместим начало координат на теле).

Она равна
(29)
где m – масса тела (спутника);

R – радиус кривизны траектории.

Помимо этой силы инерции на тело действует сила всемирного тяготения со стороны Земли, равная
(30)
где - гравитационная постоянная;

М – масса Земли;

R – это радиус Земли.

Так как тело находится на высоте r, то

Из третьего закона Ньютона получаем F=F_ЦС, откуда
(31)
Поэтому скорость спутника равна
(32)
Если тело находится на поверхности Земли, то сила притяжения равна
(33)
откуда



Поэтому
(34)
C другой стороны скорость спутника равна
(35)
Откуда

(36)
Или же
(37)
Подставляем числа (переводя одновременно все величины в СИ).

Ответ:
1.75 Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

Дано:

Найти: T=?

Решение:


Известно, что период колебаний физического маятника (ф.м. – это твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси) равно
(38)
где J – момент инерции тела относительно точки подвеса;

m – масса физического маятника;

L – расстояние от точки подвеса до центра тяжести тела (в нашем случае L=AO=R).

Для нашего случая нужно найти момент инерции диска J относительно точки подвеса А. Для того чтобы вычислить J воспользуемся теоремой Штейнера:

Если ось вращения тела параллельна оси симметрии, но смещена от нее на расстояние х, то момент инерции J относительно параллельно смещенной оси выражается соотношением
(39)
где - момент инерции тела относительно его оси симметрии. В нашем случае
(40)

a
- момент инерции диска относительно его оси симметрии,
поэтому
(41)
Тогда
(42)
Подставляем числа (переводя одновременно все виличины в систему СИ).


Ответ: