Мембранный транспорт. Лекция 7 Ж (1). Физические процессы в биологических мембранах

• Название: Физические процессы в биологических мембранах
• Анкор: Мембранный транспорт
• Дата: 08.11.2021
• Размер: 0.7 Mb.
• Имя файла: Лекция 7 Ж (1).doc
• Тип: Лекция; #266686
• страница: 1 из 2

Лекция 7.

Физические вопросы строения и функционирования мембран. Транспорт веществ через мембраны. Пассивный транспорт. Простая и об­легченная диффузия. Математическое описание пассивного транспорта.

Активный транспорт ионов. Механизм активного транспорта на при­мере натрий-калиевого насоса.

Физические процессы в биологических мембранах

Биологические мембраны являются важной частью клетки. Они ограничивают клетку от окружающей среды, защищают ее от вредных внешних воздействий, управляют обменом веществ между клеткой и ее окружением, способствуют генерации электрических потенциалов, участвуют в синтезе универсального аккумулятора энергии — аденозинтрифосфорной кислоты (АТф) в митохондриях и т. д. По существу, мембраны формируют структуру клетки и осуществляют ее функции. Нарушение функций клеточной и внутриклеточной мембран лежит в осно­ве необратимого повреждения клеток и, как следствие, развития тяжелых заболеваний сердечно-сосудистой, нервной, эн­докринной систем и пр. В главе рассматриваются физические свойства биологических мембран и основные физические процессы, которые в них происходят.
11.1. Строение и модели мембран

Все клетки окружены мембранами (цитоплазматическими, или наружными клеточными мембранами). Без мембраны содержимое клетки просто бы «растеклось», диффузия привела бы к термоди­намическому равновесию, что означает отсутствие жизни. Можно сказать, что первая клетка появилась тогда, когда она смогла отделиться от окружающей среды мембраной. Внутриклеточные мембраны подразделяют клетку на ряд замкнутых отсеков (компартаментов), каждый из них выполняет определенную функцию.

Н 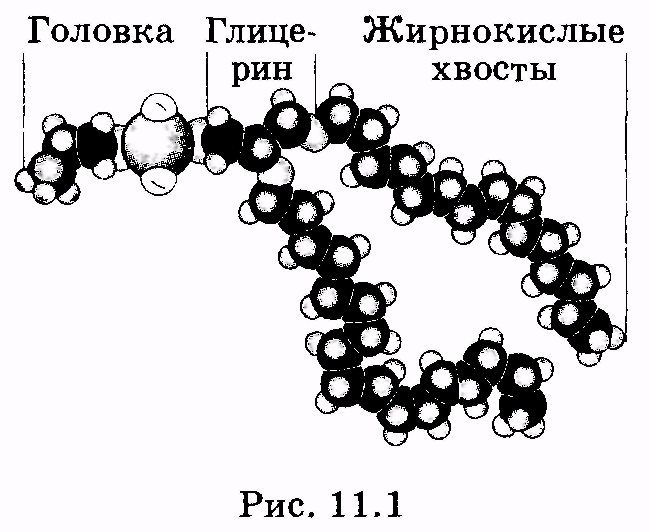есмотря на разнообразие биологических функций и форм, все мембраны построены в основном из липидов и белков. Другие соединения, встречающиеся в мембране (например, углеводы), химически связаны с липидами, либо с белками. Липидная молекула состоит из двух частей: несущей электрические заряды (полярной) головки, на которую приходится, как правило, четверть длины всей молекулы (рис. 11.1), и длинных хвостов, не несу­щих электрического заряда (гидрофобных). Хвосты липидной молекулы — это длинные цепи, построенные из атомов углерода и водорода (остатки жирных кислот). Головки могут иметь разнообразное строение, однако они заряжены либо отрицательно, либо нейтральны. Связующим звеном между хвостом и головкой чаще всего служит остаток глицерина.

Н 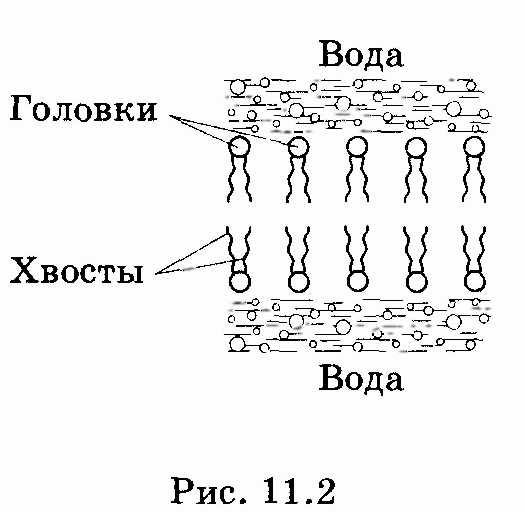абор мембранных белков, выполняющих специализированные функции, различается в цитоплазматических мембранах и мембранах внутриклеточных структур. В то же время любая мембрана своей структурной основой имеет липидный бислой, состоящий из двух мономолекулярных пленок липидов, обращенных друг к другу гидрофобными хвостами и контактирующих с окружающей средой полярными головками (рис. 11.2). Во всех мембранах бислой выполняет две основные функции: матричную и барьерную. С одной стороны, бислой является структурной основой для размещения основных рецепторных и ферментных систем клетки, с другой стороны, двойной слой липидов является преградой для ионов и водорастворимых молекул.

Первая попытка представить молекулярную организацию биологической мембраны принадлежит Даниели и Давсону, которые в 1935 г. предложили модель клеточной мембраны. Согласно этой модели, липиды располагались в два слоя (см. рис. 11.2), а поверхность липидов с обеих сторон покрывали белки. По мере приобретения новых знаний о химическом составе и физических свойствах мембран эволюционировали и представления об их организации. В настоящее время наибольшее распространение имеет предложенная в 1972 г. Синджером и Николсоном жидко-мозаичная модель, в основе которой лежит все та же липидная бислойная мембрана. Эта липидная основа представляет собой как бы двумерный растворитель, в котором плавают более или менее погруженные белки. За счет этих белков полностью или частично осуществляются специфические функции мембран — проница­емость, активный перенос через мембрану, генерация электрического потенциала и т. д. Схематично жидко-мозаичная структура мембраны показана на рис. 11.3. Здесь 1 — поверхностные белки, 2 — полупогруженные белки, 3 — полностью погруженные (ин­тегральные) белки, 4 — белки, формирующие «ионный канал» 5.

В 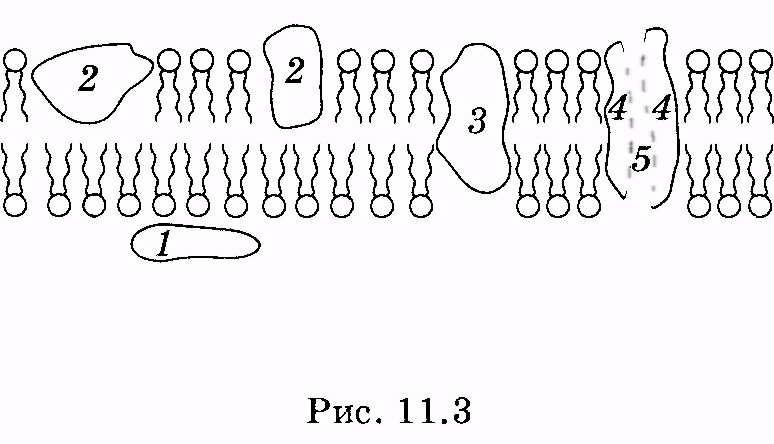целом, мембрана является динамичной структурой. Липиды могут перемещаться в плоскости мембраны (латеральная диффузия), а также переходить из одного монослоя в другой (флип-флоп переходы). При этом перемещение липидов в пределах одного мо­номолекулярного слоя происходит почти в 10 млрд раз чаще, чем флип-флоп переход. Белки также могут перемещаться в плоскости мембраны.

Уточнение строения биологических мембран и изучение их свойств оказалось возможным при использовании физико-химических моделей мембраны (искусственные мембраны). Наибольшее распространение получили три модели.
Р 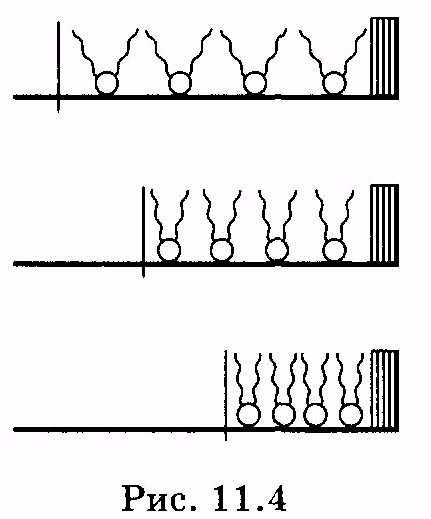ассмотрим первую модель — монослой липидов на границе раздела вода — воздух или вода — масло. На таких границах молекулы липидов расположены так, что гидрофильные головки находятся в воде, а гидрофобные хвосты — в воздухе или в масле (рис. 11.4). Если постепенно уменьшать площадь, занимаемую монослоем, в конце концов удастся получить монослой, в котором молекулы расположены так же плотно, как и в одном из монослоев мембраны. При изменении состояния липидных молекул (под действием температуры, взаимодействия липидов с различными лекарственными препа­ратами и пр.) меняется площадь, занимаемая молекулами. Поэтому в биологических и медицинских исследованиях широко используются монослои синтетических липидов, изолированных из различных природных мембран.

В 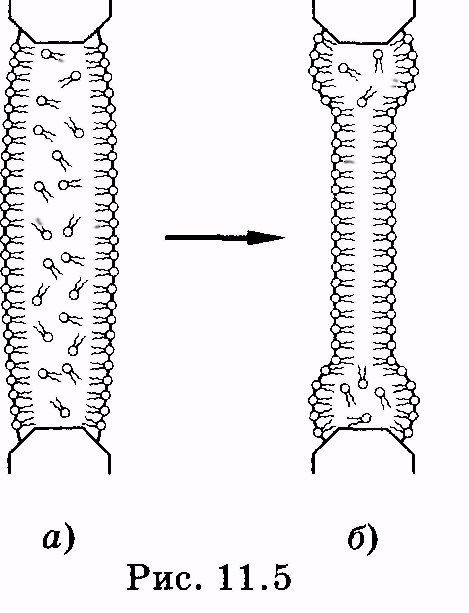торая широко использующаяся модель — бислойная липид-ная мембрана (БЛМ). Впервые такая модельная мембрана была создана в 1962 г. П. Мюллером с сотрудниками. Они заполнили отверстие в тефлоновой перегородке, разделяющей два водных раствора, фосфолипидом, растворенным в гептане (рис. 11.5, а). После того как растворитель и излишки липида растекаются по тефлону, в отверстии образуется бислой толщиной несколько на­нометров и диаметром около 1 мм (рис. 11.5, б). Расположив по обе стороны мембраны два электрода, можно измерить сопротив­ление мембраны или генерируемый на ней потенциал. Если по разные стороны перегородки поместить различные по химическо­му составу растворы, то можно изучать проницаемость мембраны для различных агентов, в том числе лекарственных препаратов.
Третьей известной моделью биологической мембраны являются липосомы. Они представляют собой мельчайшие пузырьки (ве­зикулы), состоящие из билипидной мембраны и полученные обра­боткой ультразвуком смеси воды и фосфолипидов. Липосомы фактически являются биологической мембраной, полностью ли­шенной белковых молекул. Схематически липосомы изображены на рис. 11.6

Е 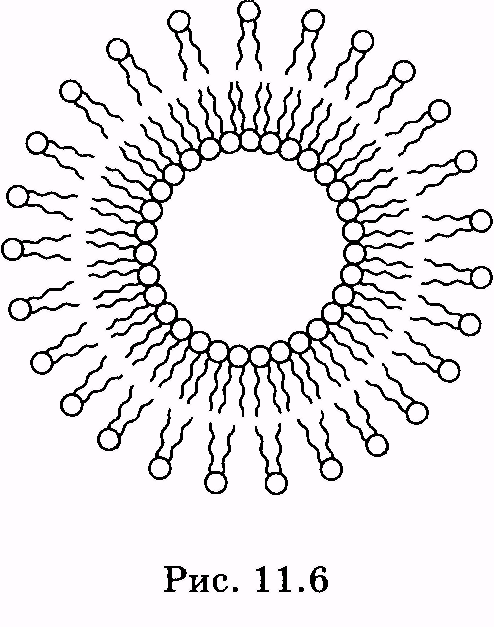сли липосомы приготовить в среде с каким-либо веществом, а затем удалить это вещество из внешней среды, то можно исследовать скорость выхода этого вещества из липосом данного липидного состава. На липосомах часто проводятся эксперименты по изучению влияния различных факторов, например состава фосфолипидов, на свойства мембраны или, наоборот, влияния мемб­ранного окружения на свойства встраиваемых белков. В медицине липосомы используют для доставки лекарственных веществ в определенные органы и ткани, приготавливая их в среде, содержащей нужное вещество. Липосомы не токсичны, полностью ус­ваиваются в организме и являются надежной липидной микрокапсулой для направленной доставки лекарства.

11.2. Некоторые физические свойства и параметры мембран

С появлением электронного микроскопа (см. § 23.2) впервые открылась возможность познакомиться со строением мембран. Тогда обнаружилось, что плазматическая мембрана животных и растительных клеток выглядит как трехслойная структура. На рис. 11.7 изображена электронная микрофотография плазматической мембраны эритроцита. Видно, что мембрана состоит из светлого слоя, соответствующего фосфолипидам бислоя, и двух темных слоев — они представляют собой полярные головки и белки. Толщина мембран в зависимости от вида составляет величину от 4 до 13 нм.

Измерение подвижности молекул мембран и диффузии частиц через мембрану свидетельствует о том, что билипидный слой ведет себя подобно жидкости. В то же время мембрана является упорядоченной структурой. Эти два фактора заставляют думать, что липиды в мембране при ее естественном функционировании находятся в жидкокристаллическом состоянии (см. § 8.2). Вязкость липидного бислоя на два порядка больше вязкости воды и соответствует приблизительно вязкости растительного масла. Однако при понижении температуры происходит фазовый переход, в результате которого липиды бислоя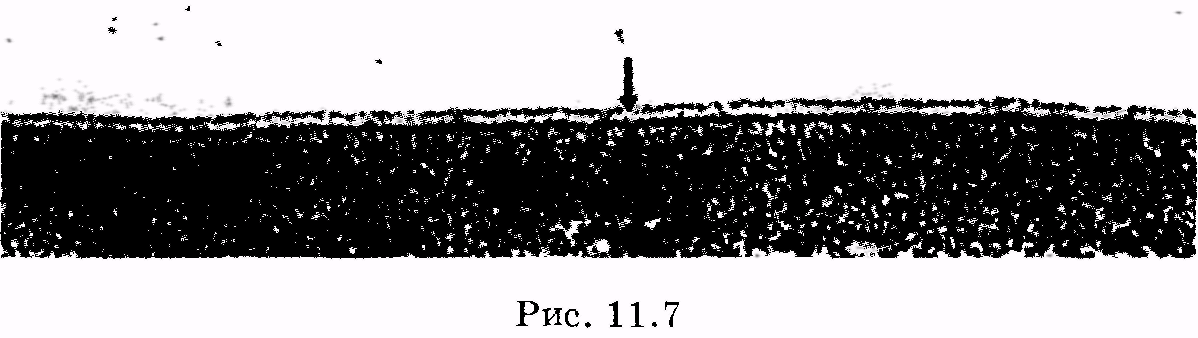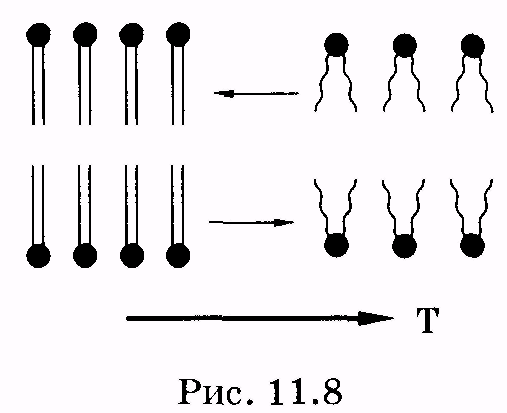
превращаются в гель (твердо-кристаллическое состояние). На рис. 8 схематически представлен процесс «пла­вления» мембранных фосфолипидов при увеличении температуры (слева направо). Очевидно, что при этом меняется толщина двойного слоя — в состоянии геля (рис. 11.8, а) она больше, чем в жидкокристаллическом (рис. 11.8, б). При фазовых переходах в бислое могут образовываться каналы, по которым через мембрану способны проходить различные ионы и низкомолекулярные соединения, размер которых не превышает 1—3 нм.

В жидкокристаллическом состоянии отдельная жирнокислотная цепь может принимать много различных конфигураций из-за вращения вокруг С—С связей. При том возможно образование в бислое полостей — «кинков» (от англ, kink— петля). В этих полостях могут находиться различные молекулы, захваченные из пространства вне мембраны. При тепловом движении хвостов липидов происходит движение такого «кинка», а вместе с ним и мо­лекул поперек мембраны или вдоль нее (рис. 11.9).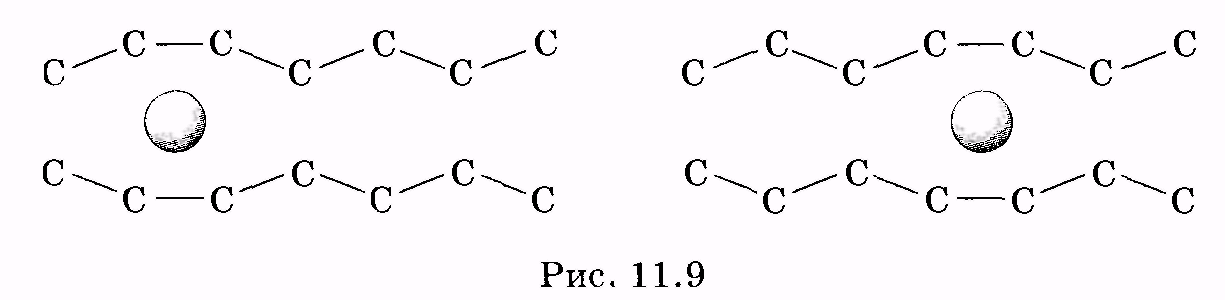



Проницаемость мембран для различных веществ зависит от поверхностного заряда, который создается заряженными головками липидов, придающими мембране преимущественно отрицательный заряд. Это приводит к тому, что на границе мембрана — вода созда­ется межфазный скачок потенциала (поверхностный потенциал) того же знака, что и заряд на мембране. Величина этого потенциала играет большую роль в процессах связывания ионов мембраной. Помимо поверхностного потенциала, для нормального функциони­рования ферментных и рецепторных мембранных комплексов огромное значение имеет трансмембранный потенциал, природа ко­торого будет рассмотрена ниже. Величина этого потенциала составляет 60—90 мВ (со знаком минус со стороны цитоплазмы). Из-за очень малой толщины мембран напряженность электрического поля в них достигает величины около (6—9) • 10⁶ В/м.

Мембрана по своей структуре напоминает плоский конденсатор, обкладки которого образованы поверхностными белками, а роль диэлектрика выполняет липидный бислой. Емкость такого конденсатора составляет значительную величину (табл. 18). Используя формулу плоского конденсатора, можно оценить диэлектрическую проницаемость  гидрофобной и гидрофильной областей мембран, зная пределы изменения толщины мембраны. Такие оценки дают для фосфолипидной области мембраны значение  = 2,0—2,2, а для гидрофильной части  = = 10—20.

В табл. 18 приведены некоторые физические параметры биологических мембран и в сравнении с ними — те же параметры для искусственно приготовленных липидных бислоев.
Таблица 18.физические свойства биологических мембран и липидных бислоев

Физические параметры	Биологические мембраны	Липидные бислой
Толщина, нм	4—13	4,6—9,0
Электрическое сопротивление, Ом • см2	102— 105	103— 109
Электроемкость, мкФ • см-2	0,5—1,3	0,3—1,3
Потенциал покоя, мВ	20—200	0—140
Показатель преломления	1,55	1,37
Поверхностное натяжение, мН • м-1	0,03—3	0,2—6,0
Коэффициент проницаемости для воды,
10 4 см • с-1	25—33	5—10
Напряжение пробоя, мВ	100	150—200
Плотность липидного бислоя, кг/м3	800	760—900
Эффективный модуль упругости, Па	0,45	0,3—0,5

Мембраны обладают высокой прочностью на разрыв, устойчи­востью и гибкостью. По электроизоляционным свойствам они значительно превосходят многие изоляционные материалы, при­меняемые в технике. Общая площадь мембран в органах и тканях достигает огромных размеров. Так, суммарная площадь клеточ­ных мембран печени крысы, весящей всего 6 г, составляет не­сколько сотен квадратных метров. Клетки, как правило, имеют микроскопические размеры, поэтому отношение их поверхности к объему очень велико. Благодаря этому клетки располагают до­статочной площадью для обеспечения многочисленных процес­сов, протекающих на мембранах. Одним из наиболее важных из них является процесс переноса веществ из клетки и в клетку.
11.3. Перенос молекул (атомов) через мембраны. Уравнение Фика

Важным элементом функционирования мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Существенно, что вероятность такого проникновения час­тиц зависит как от направления их перемещения, например в клетку или из клетки, так и от разновидности молекул и ионов.

Эти вопросы рассматриваются в разделе физики, относящемся к явлениям переноса. Таким термином называют необратимые процессы, в результате которых в физической системе происхо­дит пространственное перемещение (перенос) массы, импульса, энергии, заряда или какой-либо другой физической величины.

К явлениям переноса относят диффузию (перенос массы вещест­ва), вязкость (перенос импульса), теплопроводность (перенос энер­гии), электропроводность (перенос электрического заряда). Здесь и в следующих параграфах рассматриваются наиболее существенные для биологических мембран явления: перенос вещества и перенос заряда. Как синоним переноса частиц в биофизике широкое распро­странение получил также термин транспорт частиц.

Выведем основное уравнение диффузии (уравнение Фика), рассматривая процесс переноса в жидкостях.

П 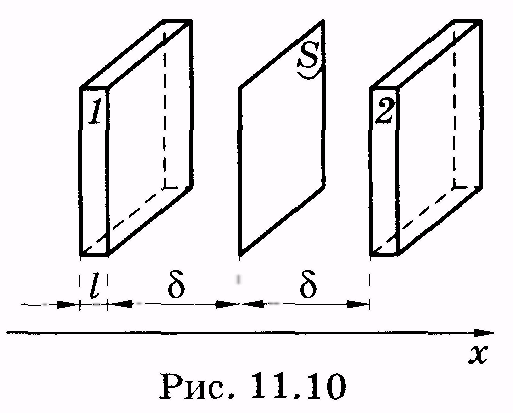усть через некоторую площадку S (рис. 11.10) во всех направ­лениях перемещаются молекулы жидкости. Учитывая теорию молекулярного строения жидкости (см. § 7.6), можно сказать, что молекулы пересекают площадку, перескакивая из одного положе­ния равновесия в другое.

На расстояниях, равных среднему перемещению  молекул (сред­нее расстояние между молекулами жидкости), вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины l(l<< ). Объем каждого параллелепипеда равен Sl. Если п — концентрация молекул, то внутри выделенных параллелепипедов имеет­ся Slnмолекул. Предположим, что кон­центрация молекул изменяется в про­странстве, в левом (1) выделенном па­раллелепипеде концентрация равна п₁, а в правом (2) — п₂. Следовательно, в одном параллелепипеде Sln_lмолекул, а в другом — Sln₂молекул.

Все молекулы вследствие хаотичного их движения можно ус­ловно представить шестью группами, каждая из которых пере­мещается вдоль или против направления одной из осей коор­динат. Отсюда следует, что в направлении, перпендикулярном площадке S, вдоль оси ОХ от первого параллелепипеда переска­кивает ¹/₆ Sln_lмолекул, а противоположно оси ОХ от второго па­раллелепипеда перескакивает ^l/₆Sln₂молекул.

Время t< «пролета» этими молекулами площадки S может быть найдено следующим образом. Предположим, что все молеку­лы из выделенных объемов движутся с одинаковыми средними скоростями <>. Тогда молекулы в объеме 1 или 2, дошедшие до площадки S, пересекают ее в течение промежутка времени

t = l/<>. (11.1)

Подставляя в (11.1) выражение для средней скорости <>= ,

получаем

(11.2)
где  — среднее время «оседлой жизни» молекулы, оно может рассматриваться как среднее время перескока. «Баланс» переноса молекул через площадку S за промежуток времени tравен

(11.3)

Умножая (11.3) на массу т отдельной молекулы и деля на t,находим массовый поток сквозь площадку S:

(11.4)

т. е. масса вещества, которая за 1 с переносится через площадку S. Изменение концентрации п₂- n_lмолекул можно представить как произведение dn/dxна расстояние 2 между выделенными объ­емами:

(11.5)

В уравнении (11.4) заменим tсогласно (11.2) и (п₂ – п₁)со­гласно (11.5):

(11.6)

Отношение потока к площади S, через которую он перено­сится, называется плотностью потока:

(11.7)

Произведение массы молекулы на их концентрацию есть плот­ность вещества (парциальная плотность):

(11.8)

Учитывая это, имеем из (11.7)



Это есть уравнение диффузии (уравнение Фика), которое обычно записывают в виде:

(11.9)

Знак «-» показывает, что суммарная плотность потока вещества при диффузии направлена в сторону уменьшения плотности (в сторону, противоположную градиенту плотности), D— коэффи­циент диффузии, применительно к рассмотренному примеру диффузии в жидкости он равен

(11.10)

Как видно из (11.10), единица измерения коэффициента диффу­зии [м²/с].

У равнение диффузии можно записать не только для плотности массового потока но и для плотности потока частиц и плотности потока вещества при этом в уравнении(11.9) вместо градиента плотности следует использовать соответственно градиент концентрации или градиент молярной концентрации :

(11.11)
А. Эйнштейн показал, что коэффициент диффузии пропорци­онален температуре:

(11.12)

И поэтому вместо (11.11) имеем

(11.13)

В формуле (11.12) и далее и_т— подвижность диффундирующих молекул (частиц), выраженная для моля. Вообще говоря, подвиж­ностью диффундирующей частицы (молекулы, атома, иона, электрона) и называют коэффициент пропорциональности между скоростью частицы и силой f, двигающей частицу, в том случае, когда на частицу не действуют другие силы (например, трение или соударение с другими частицами) и она перемещается равномерно:

 = ufили и = /f.(11.14)

Как видно из (11.14), единица подвижности 1 м/(с • Н). Величины и_ти и связаны через постоянную Авогадро:

и = и_mN_A. (11.15)

П 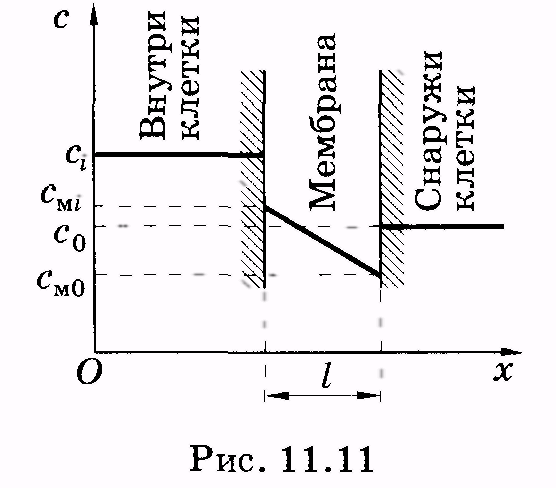реобразуем уравнение (11.9) применительно к биологической мембране. Будем считать, что концентрация частиц, диффунди­рующих через мембрану, изменяется в мембране по линейному закону (рис. 11.11). Молярные концентрации частиц внутри и вне клетки соответственно равны c_iи с₀. Молярная концентрация этих же частиц в мембране изменяется от внутренней к наружной ее части соответственно от с_мiдо с_м0. Учитывая линейное измене­ние концентрации молекул, запишем

(11.16)

где l — толщина мембраны, тогда вместо (11.11) имеем

(11.17)

Практически доступнее определить молярные концентрации час­тиц не внутри мембраны (с_мiи с_м0), а вне мембраны: в клетке (c_i) и снаружи клетки (с₀). Считают, что отношение граничных значений концентраций в мембране равно отно­шению концентраций в прилегающих к мембране слоях: с_м0/ с_мi = c₀/c_i; откуда

(11.18)

где k— коэффициент распределения вещества (частиц) между мембраной и окружающей средой (обычно водная фаза). Из (11.18) следует

(11.19)

Подставляя (11.19) в (11.17), имеем


Пусть

Р = Dk/l, (11.20)

где Р — коэффициент проницаемости. В результате получаем уравнение для плотности потока вещества при диффузии через биологическую мембрану:

J = P(с_i - c₀). (11.21)