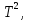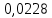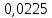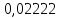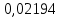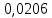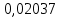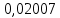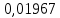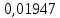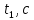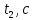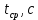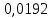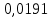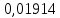Физический маятник(135). Физический маятник
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
|
Нижегородский государственный университет им. Н. И. Лобачевского Радиофизический факультет Отчёт по лабораторной работе №135: Физический маятник Выполнил: Козлов А. Д - студент 417 группы Проверил: Менсов С. Н. – Доцент кафедры общей физики Нижний Новгород 2021 г. Теоретическое обоснование: Цель работы: произвести замеры периодов колебаний при различных амплитудах, построить график зависимости T2(a), определить приведённую длину математического маятника. Приборы и оборудование: установка МАЯТНИК УНИВЕРСАЛЬНЫЙ ФМ-13, линейка. Введение: 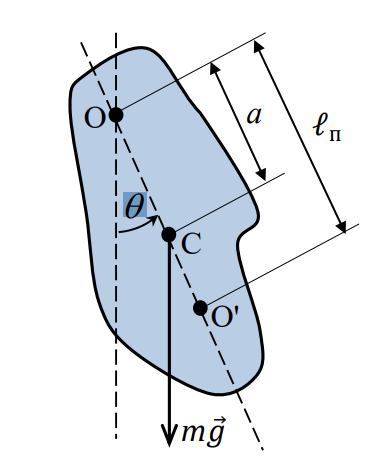 Физический маятник – это твёрдое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Физический маятник – это твёрдое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести.В данной лабораторной работе исследуется зависимость периода колебаний физического маятника от расстояния его центра масс и точкой подвеса. Рассмотрим твердое тело произвольной формы, совершающее колебания в поле тяжести вокруг горизонтальной оси О (рис. 1). Запишем уравнение вращательного движения тела в виде: 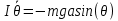 (1), (1),где I – момент инерции тела относительно оси О, m - масса тела, a – расстояние от оси до центра масс С, θ – угол отклонения прямой ОС от вертикали. При малых углах отклонения (θ<<1) можно положить sin и свести уравнение (1) к уравнению гармонического осциллятора (2): Рис.1 Физический маятник  (2) (2)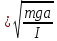 - собственная (круговая) частота. - собственная (круговая) частота.Решением данного уравнения является функция  (3), описывающая гармонические колебания. Амплитуда A и начальная фаза (3), описывающая гармонические колебания. Амплитуда A и начальная фаза  колебаний определяются начальными условиями. Период T находится по формуле: колебаний определяются начальными условиями. Период T находится по формуле: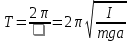 (4) (4)Входящий в формулу (4) момент инерции I относительно оси О можно выразить по теореме Гюйгенса-Штейнера через момент инерции  относительно оси, проходящей через центр масс С, как: относительно оси, проходящей через центр масс С, как: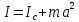 (5) (5)Подставляя формулу (5) в формулу (4), находим зависимость периода колебаний физического маятника от расстояния a: 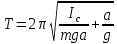 (6) (6)Зависимость T от a далее будем исследовать экспериментально. Приведенной длиной физического маятника п называется длина такого математического маятника, период колебаний которого равен периоду колебаний физического маятника. Сравнивая формулы (4) и (6) с формулой для периода математического маятника 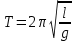 , получаем: , получаем: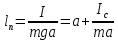 (7) (7)Точка О', лежащая на прямой ОС на расстоянии п от оси вращения (рис. 1), называется центром качания. Точки О и О' являются сопряженными: если физический маятник подвесить в точке О', то новым центром качания станет точка О, а период колебаний маятника не изменится (теорема Гюйгенса). Экспериментальная установка: В  экспериментальной установке используется физический маятник в виде стержня, на котором с помощью фиксирующих винтов закрепляют в выбранных точках треугольную призму-опору (П) и утяжеляющий груз (чечевицу Ч) (рис. 2). Маятник подвешивается на вертикальной стойке, установленной на массивной подставке. Для этого на стойке имеется горизонтальная платформа, на которую опирается закрепленная на стержне призма. Ребро призмы является осью вращения маятника. На стержне маятника с интервалом в 1 см сделаны кольцевые насечки для измерения расстояний. К горизонтальной платформе также подвешен с помощью двух нитей массивный шарик, выполняющий роль математического маятника. На вертикальной стойке закрепляется кронштейн с фотоэлектрическим датчиком, отмечающим прохождение маятником (стержнем или шариком) вертикального положения. Электронное устройство подсчитывает число полных циклов колебаний, совершенных с момента нажатия кнопки «ПУСК» до нажатия кнопки «СТОП», и измеряет общее время этих циклов. При изменении длины маятника кронштейн необходимо передвинуть так, чтобы маятник оказался в рабочей зона датчика. экспериментальной установке используется физический маятник в виде стержня, на котором с помощью фиксирующих винтов закрепляют в выбранных точках треугольную призму-опору (П) и утяжеляющий груз (чечевицу Ч) (рис. 2). Маятник подвешивается на вертикальной стойке, установленной на массивной подставке. Для этого на стойке имеется горизонтальная платформа, на которую опирается закрепленная на стержне призма. Ребро призмы является осью вращения маятника. На стержне маятника с интервалом в 1 см сделаны кольцевые насечки для измерения расстояний. К горизонтальной платформе также подвешен с помощью двух нитей массивный шарик, выполняющий роль математического маятника. На вертикальной стойке закрепляется кронштейн с фотоэлектрическим датчиком, отмечающим прохождение маятником (стержнем или шариком) вертикального положения. Электронное устройство подсчитывает число полных циклов колебаний, совершенных с момента нажатия кнопки «ПУСК» до нажатия кнопки «СТОП», и измеряет общее время этих циклов. При изменении длины маятника кронштейн необходимо передвинуть так, чтобы маятник оказался в рабочей зона датчика.Практика и расчёты: Физические характеристики приборов установки: масса чечевицы 315 грамм, масса стержня 199 грамм, длина стержня 44 сантиметра. Абсолютные погрешности приборов:  , ,  Задание №1: Расстояние от конца стержня до центра чечевицы  сантиметра. сантиметра.Расстояние от конца стержня до центра масс маятника 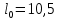 сантиметров. сантиметров.Задание №2:
Зависимость периода колебаний T от расстояния h (от конца стержня до ребра призмы). Таблица 1: измерения зависимости периода от расстояния 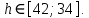

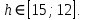
 Вычисление погрешностей при подсчёте квадратов периодов, запишем общую формулу:  , где , где 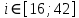  (8) (8)Подставляя в формулу (8) найдём погрешности измерения периодов в квадрате:   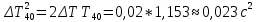 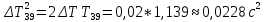  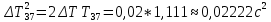 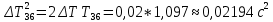 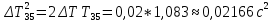    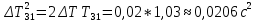   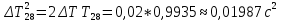  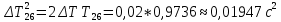   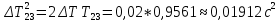 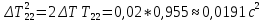  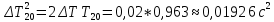  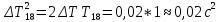   Задание №4: Подвешиваем физический маятник так, чтобы период колебаний был минимален и определяем соответствующую приведённую длину 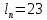 сантиметра. сантиметра.Задание №3: График зависимости T2(a): 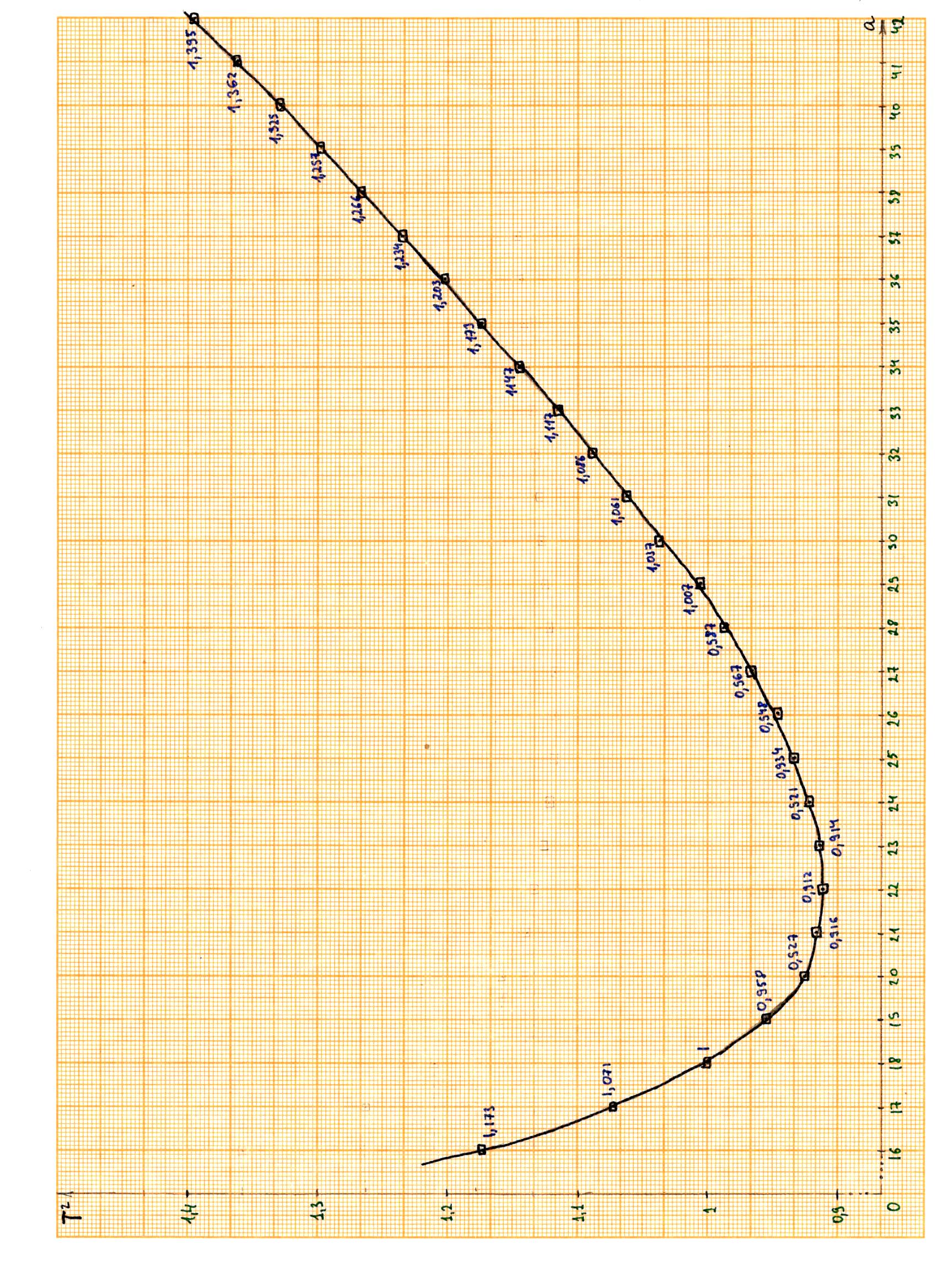  Протокол лабораторной работы Вывод: В ходе выполнения работы мы вычислили центр масс физического маятника, выявили зависимость периода колебаний от расстояния между точкой крепления и центром масс маятника. Построили график зависимости квадрата периода от расстояния между точкой крепления и центром масс маятника. Определили приведённую длину математического маятника при минимальном периода колебания физического маятника. Ответы на контрольные вопросы: Доказать, что суммарный момент распределённой по объёму физического маятника силы тяжести равен моменту суммарной силы тяжести, приложенной к центру масс маятника. Ответ:   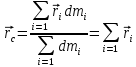 при равных dmi при равных dmiСледовательно:  Доказать сопряжённость точек O и  (Теорему Гюйгенса). (Теорему Гюйгенса). Ответ: Ответ:Запишем выражение для приведённой длины в точке O  Выразим из выражения приведённой длины момент инерции  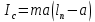 Теперь перейдём в точку   Следовательно, 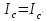 , точки O и , точки O и  сопряжённые. сопряжённые.Получить из формулы (6) выражения для  через через  и m. и m.Ответ: 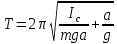 (6) (6)Вычислим производную 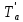 : : Найдём нули производной 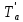 : :  Вычислим 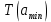 : :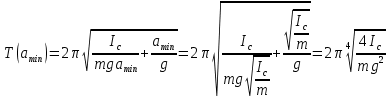 Получить теоретически, чему равно отношение 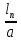 при при  . .Ответ: 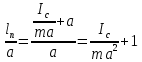 При  получим: получим: Получить формулу для расчёта ускорения свободного падения g без использования графика T2(a) – по данным измерений T при двух значениях a. Какие значения a следует брать при получении наибольшей точности расчёта? Ответ: Запишем формулу периода колебаний физического маятника:  Получим выражение:  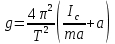 |

 , с
, с , с
, с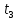 , с
, с , с
, с , с
, с