Физик а автор составитель, Лукина Галина Степановна, методист хкцтт

• Название: Физик а автор составитель, Лукина Галина Степановна, методист хкцтт
• Дата: 26.09.2018
• Размер: 487.5 Kb.
• Имя файла: 2008_k1_p_10.doc
• Тип: Документы; #51711

Ф И З И К А

Автор – составитель, Лукина Галина Степановна, методист ХКЦТТ

ЭЛЕМЕНТЫ СТАТИКИ

По учебному плану Хабаровской краевой заочной физико-математической школы в новым учебном году занятия физикой будут проводиться с акцентом на теме «Элементы статики». Эта тема включена в школьные программы только в классах с профильным обучением. Поэтому для учащихся общеобразовательных классов решение задач с использованием законов равновесия может представляться довольно сложным. Повторением этих законов мы и будем заниматься с учащимися старших классов в течение этого учебного года.

Для получения зачета по данной сессии минимальная сумма баллов для учащихся любого класса – 10. Для получения отличной оценки – 30 баллов.

И, как и в прошлые годы, учащимся младших классов предлагаем продолжить наблюдение за окружающим нас миром.

Учащимся 7-8 классов

Мир, в котором мы живем

Природа всегда неохотно отдает свои тайны. И пора­зительно не то, что существуют многочисленные вопросы, задаваемые нам самой природой, а то, что мы можем находить на них ответы. Приобретая новые знания, мы можем судить о предметах, совершенно удаленных во времени и в пространстве, например, о том, что происходило, допустим, во Вселенной 14 миллиардов лет назад. Ньютон, один из величайших гениев, писал: «Не знаю, кем я могу казаться этому миру, но самому себе я кажусь мальчиком, играющим на морс­ком берегу. Время от времени я... нахожу на берегу камешки и ракушки... в то время как великий океан Истины остается для меня полностью неисследован­ным».

Физика нас окружает повсюду - дома, на улице, в поле, в лесу, у реки. Нужно только уметь видеть, замечать и задавать вопросы. И каждый ответ на поставленный перед собой вопрос станет маленьким, но открытием, открытием мира для себя!

Для начала пред­лагаем вам заняться опытами. Для этого можно использовать буквально все, что нахо­дится под рукой, либо внимательно наблю­дать за окружающими вас явлениями. Вы убедитесь, что за многими, совсем простыми на первый взгляд событиями кроется вполне серьезная физика, требующая размышлений и смекалки.

Задание 1. (Каждый обоснованный ответ задания 1 оценивается 2 баллами. Для зачета по этому разделу нужно набрать не менее 10 баллов. При этом обязательно писать вначале сам вопрос, и только потом – ответ на него. Порядок вопросов значения не имеет.)

1. Посидите на табуретке, а затем пересядьте в кресло. Почувствовали разницу?

Вопрос: Почему в кресле сидеть удобнее?

2. Возьмите в руки два яйца – одно сырое, другое – сваренное вкрутую.

Вопрос: Можно ли, не разбивая скорлупы куриного яйца, узнать, сырое оно или вареное?

3. Выдуйте в трубочку мыльный пузырь. Понаблюдайте за его движением. Куда он движется – вверх или вниз? Проделайте этот же опыт в более холодном помещении.

Вопрос: Почему мыльный пузырь движется так, как вы это увидели? В каком помещении он движется быстрее – в холодном или теплом?

4. Возьмите в руки веревочку и сложите ее в несколько слоев. Взявшись за один конец, отпустите веревочку. Она повиснет. Теперь завяжите ее узлом или бантиком.

Вопрос: Почему узел крепко держит связанные им куски веревки?

5. Положите на вытянутые пальцы линейку так, чтобы она сохраняла равновесие. Теперь сдвигайте пальцы. Что происходит с линейкой? Какие возможны варианты ее движения?

Вопрос: Почему нарушается равновесие линейки при изменении точек ее опоры и в какую сторону?

6. Сядьте на стул так, чтобы спина и ноги были расположены вертикально. А теперь попробуйте встать со стула, не изменяя положения спины и ног.

Вопрос: Почему, вставая со стула, мы либо подаемся туловищем вперед, либо пододвигаем под стул ноги?

7. Возьмите стальную иголку и опустите ее в чашку с водой.

Вопрос: Можно ли добиться того, чтобы стальная игла плавала на поверхности воды? Если можно, то, как это сделать?

8. Поставьте на окно банку с водой и посмотрите сквозь нее на улицу. Какими вы видите предметы на улице? Отойдите от банки на шаг и снова посмотрите сквозь нее на улицу. Изменилось ли что-нибудь в увиденной картине? Вопрос: Как вы можете объяснить наблюдаемое явление?

9. Поставьте детскую игрушку неваляш­ку на шерохова­тую доску и приподнимите правый край доски.

Вопрос: В какую сторону откло­нится «голова»» игрушки при сохране­нии ее равновесия? _{Почему?}

10. Принимая ванну, попробуйте определить, какая вода – прохладная или горячая – держит вас лучше?

Вопрос: Может ли дерево, плавающее в холодной воде, утонуть в горячей воде?

Учащимся 7-10 класса

Задание 2. (Каждый ответ оценивается 2 баллами.)

1. Все мы увлекаемся или увлекались в свое время фантастикой. Давайте пофантазируем и сейчас: что произошло бы на Земле, если бы воздух внезапно исчез? Перечислите главные последствия исчезновения воздуха - что стало бы…

а) с температурой Земли;

б) с водными пространствами Земли;

в) со звуком на Земле;

г) цветом неба;

д) панорамой неба;

е) жизнью человека, фауны и флоры?

2. 
   Назовите самый легкий и самый тяже­лый камень на Земле. Чем обусловлен вес камня?
   
3. 
   Если надо быстро загасить образовавшееся пламя, то какой водой лучше его заливать - холодной или горячей? Почему?
   
4. 
   Обычно летом дождевые капли крупные, а осенью мелкие. Почему?
   

5. С какой скоростью упадет на землю пуля, выпу­щенная из винтовки вертикально вверх?

6. Сколько километров вы пролетели в мировом пространстве за время, пока вы читали этот вопрос?

Задание 3. Задачи – оценки. (Каждая задача оценивается в10 баллов)

Задача 1.С.А.Тихомирова, в статье «Архимедова сила в литературных произведениях» в журнале «Квант» приводит отрывок из книги «Детские годы Багрова-внука» С.Т. Аксакова, в котором описывается, как во время ледохода какая-то несчастная черная корова бегала по льдине, как безумная.

Оцените, каковы минимальные размеры льдины, на которой могла плыть корова. Прикиньте сами, чему равна масса коровы и толщина льда.

Задача 2.В этой же статье приводятся строки из произведения Н.А. Некрасова «Дедушка Мазай и зайцы»

«Мимо бревно суковатое плыло» Сидячи, стоя, и лежа пластом, Зайцев с десяток спасалось на нем.

«Взял бы я вас - да потопите лодку!» Жаль их, однако, да жаль и находку – Я зацепился багром за сучок И за собою бревно поволок...»

Оцените, при каком минимальном объеме бревна зайцы могли на нем плыть. Прикиньте сами, чему равна масса зайца.

Учащимся 8-11 класса

Задание 4. Экспериментальные задачи.

Э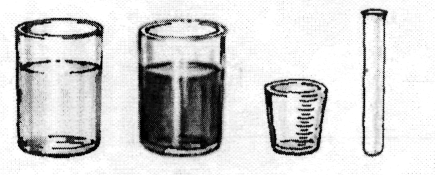то задание рассчитано на учащихся, которые готовятся к олимпиадам по физике различного уровня – от школьного до зонального Предлагаем для решения любую из трех экспериментальных задач, Для их решения требуют­ся и сообразительность, и умелые руки, и прочные знания школьного курса физики. Проверьте себя! Решение каждой задачи оценивается 10 баллами

Задача 1 (9-11 класс). Определите плотность неизвестной жидкости.

Оборудование: сосуд с водой, сосуд с неизвестной жидкостью (с раствором соли), мензурка, про­бирка.

З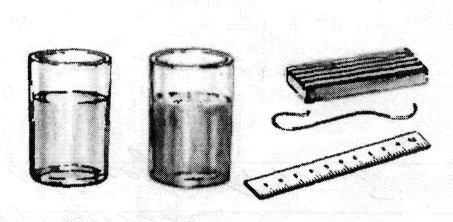адача 2 (10-11 класс). Сравните коэффициенты поверх­ностного натяжения воды и мыльного раствора.

Оборудование: стеклянная трубка, пластилин, кусок проволоки, сосуд с водой, сосуд с мыльным рас­творам, линейка.

Задача 3 (11 класс). Определите разрешающую способ­ность глаза и исследуйте ее зависи­мость от диаметра отверстия в экра­не, помещенном перед ним.

О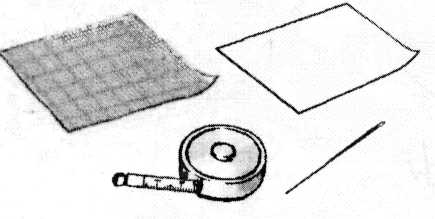борудование: лист мил­лиметровой бумаги, лист белой бу­маги, игла, рулетка или метровая линейка.

Решение должно сопровождаться:

1. кратким описанием теоретических положений, используемых для решения;

2. 
   планом и порядком выполнения работы;
   
3. 
   полученными результатами в виде вычислений или графиков;
   
4. 
   оценкой погрешности измерений.
   

Учащимся 9-11 класса.

1. Основные понятия статики

1.1. Центр масс. Одно из основных понятий статики – центр масс.

Центр масс существует у любого тела, более того - у любой системы тел. Он обладает замечательными свойствами, о которых мы будем говорить в следующих номерах нашего журнала.

Рассмотрим произвольную механическую систему твердых тел с заданным взаимным расположением в пространстве и с известными массами. Поступательное дви­жение такой системы под действием внешних сил эквивален­тно движению материальной точки, имеющей массу, равную массе системы, и находящейся под воздействием результиру­ющей силы всех внешних сил. Геометрическую точку, в которой располагается эта материальная точка, называют центром инерции или центром масс данной системы. Итак, центром масс тела или системы тел называется точка, которая движется так, как будто бы в ней сосредоточена вся масса тела.

Начнем с определения положения центра масс. Для произвольной неподвижной прямоугольной системы коор­динат (ее называют также лабораторной системой) коорди­наты центра масс определяются следующими формулами: x_С=x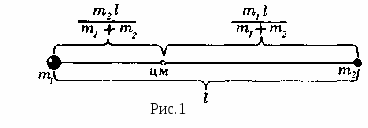_i, y_С==y_i, z_С==z_i, где m_i, x_i, y_i, z_i - массы и координаты центров масс тел, входящих в систему, а М - суммарная масса всех тел. Расчет выглядит так: x_C=; аналогично для координат y_C и z_C.

а) В случае двух точек массами m₁и m₂ выражение для x_C имеет наглядный смысл: центр масс лежит между точками, ближе к той, у кото­рой масса больше (рис.1); отношение расстояний до точек обратно отноше­нию их масс (проверьте это сами). В общем случае центр масс лежит где-то между точками сис­темы, отражая распределение масс в пространстве.

б) В определении положе­ния центра масс все материальные точки «участвуют» совершенно равно­правно. Значит, если расположение масс симметрично относительно ка­кой-то точки, то эта точка и будет центром масс. Например, центр масс однородного шара совпадает с его центром (то же для цилиндра, куба и т. п.).

П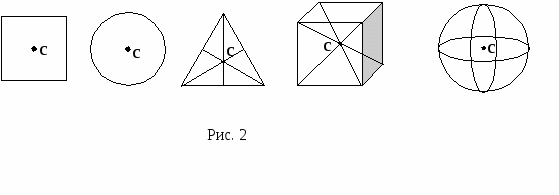
оэтому центр масс фигур и тел правильной геометрической формы совпадает с геометрическим центром (рис. 2).

в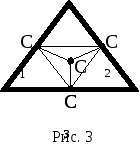) Еще одно очень важное замечание: положение центра масс не изменится, если мы, выделив какую-то часть рассматриваемой системы, сосредоточим всю массу этой части в одной точке – ее центре масс. Например, центр масс проволочного треугольника совпадает с центром масс системы трех точек, расположенных в серединах сторон этого треугольника (рис.3).

Если сумма внешних сил, действующих на систему, рав­на нулю, то центр масс остается неподвижным или движет­ся прямолинейно с некоторой постоянной скоростью (в зависимости от предыстории). В этом случае удобно рас­сматривать движение тел под действием внутренних сил в инерциальной системе отсчета, связанной с центром масс. В такой системе отсчета импульс системы равен нулю и будет оставаться нулевым при любых взаимодействиях меж­ду телами системы.

1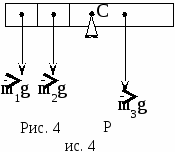.2. Центр тяжести. В повседневной жизни мы часто прибегаем не к понятию центра масс, а к понятию центра тяжести. Для тел, размеры которых очень малы по сравнению с радиусом Земли, силы тяжести, действующие на от­дельные частицы тела, можно счи­тать параллельными друг другу и направленными вертикально вниз. Равнодействую­щая всех элементарных сил тяжести есть сила тяжести, действующая на все тело. Направлена сила тяжести вертикально вниз.

Приложена эта сила к центру масс, так как любое тело, падающее сво­бодно (под действием только силы тяжести), движется поступательно. Поэтому центр масс называют цент­ром тяжести тела.

Итак, центром тяжести твердого тела называется точка, в которой при­ложена равнодействующая сил тя­жести, действующих на частицы дан­ного тела.

В основе расчета его местоположения в большинстве случаев лежит основное свойство центра тяжести: суммарный момент всех составляющих сил тяжести относительно оси, проходящей через центр тяжести тела, всегда равен 0: М_С = 0. Здесь С – центр тяжести тела или системы тел. Если тело закрепить в точке С, то оно будет находиться в равновесии. То есть, тело находится в равновесии, если центр вращения его находится в центре тяжести. Именно это свойство положено в основу расчета положения центра тяжести в большинстве задач (рис. 4).

Нужно отметить, что центр тяже­сти может лежать и вне пределов данного тела (например, для кольца, согнутого тонкого стержня и т. п.).

Найти центр тяжести однородного тела (или центр масс) часто помогают соображения симметрии. Если тело имеет пло­скость, ось или центр симметрии, то центр тяжести лежит соответственно в плоскости, на оси или в центре симметрии. Так, центр тяжести однородного круглого кольца, круглого диска, тонкого стержня, прямоуголь­ной пластины, шара находится в их центре симметрии (рис. 1).

1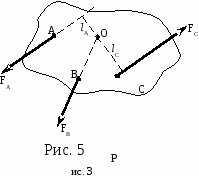.3. Момент силы. Вращательное действие, вызванное какой-либо силой, зависит не только от модуля этой силы, но и от расстояния от оси до линии действия силы. Кратчайшее расстояние от оси вращения (или точки вращения) до линии действия силы называют плечом силы, а так как кратчайшим расстоянием является перпендикуляр, то плечом является перпендикуляр, опущенный из центра вращения на направление силы. Обозначают плечо силы чаще всего буквой l (или L) (рис.5).

Моментом силы относительно оси называется физическая величина, численно равная произведению абсолютной величины (модуля) силы на плечо этой силы.

Момент силы – величина векторная, определяемая векторным произведением силы на плечо. Но так как это математическое действие в школьном курсе не изучается, упростим расчетную формулу момента силы: M = Fl.

И договоримся о знаке момента. Внешние силы могут вращать тело вокруг оси в противоположные стороны, поэтому моменту силы будем при­писывать знак «+» или « - ». Услов­но примем моменты сил, стремя­щиеся повернуть тело против часовой стрелки, брать со знаком «+», а по часовой - со знаком « - » (в соот­ветствии с правилом отсчета углов). Момент силы F_А (рис.5) положителен, так сила F_А стремится повернуть тело вокруг центра вращения 0 против часовой стрелки, М_А 0; момент силы F_В равен 0, так как плечо этой силы равно 0, М_В=0; момент силы F_С отрицателен, так как эта сила стремится повернуть тело вокруг центра вращения 0 по часовой стрелке, М_С 0.

В случае, если все действующие силы расположены в одной плоскости (плоской системы сил), можно вместо момента силы относи­тельно оси, перпендикулярной к плоскости действия сил, говорить о моменте силы относительно точки вращения, имея в виду точку пересечения этой оси с плоскостью.

1.4. Основные силы, действующие на тело в состоянии равновесия

а) Прежде всего надо назвать силу тяжести. Ли­ния действия силы тяжести прохо­дит через центр масс тела - центр тяжести.

б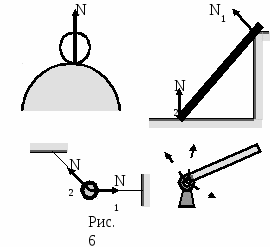) Реак­ции связей - силы, препятствующие перемещению тела в каком-нибудь направлении (рис. 6). Направление дейст­вия реакции связей противоположно тому направлению, в котором связь препятствует перемещению данного тела. Реакции связей - это силы упругости и силы трения. Особен­ность их в том, что абсолютное зна­чение их, а иногда и направление, наперед не известны и зависят от формы тел, состояния поверхностей, а также от других сил, действующих на тело. Правильное определение направ­ления сил реакции играет при реше­нии задач статики очень важную роль.

Поэтому рассмотрим, как направ­лены реакции некоторых видов связей.

1. Тело опирается на гладкую поверхность или опору. Трение от­сутствует. Когда соприкосновение те­ла с опорой происходит в одной точ­ке, сила реакции поверхности прило­жена в точке касания тел и направ­лена либо по общей нормали к поверх­ностям соприкасающихся тел в точке их касания, либо по нор­мали к поверхности тела или к по­верхности опоры. Такую реакцию называют нормальной.

2. Связь осуществляется гибкой нитью. Сила реакции нити всегда направлена вдоль нити от той точки, в которой нить прикрепляется к телу.

3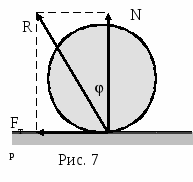. Шарнирная связь - цилинд­рический шарнир, в котором ось шар­нира перпендикулярна плоскости действия сил. Реакция такого шарнира может иметь любое направление в плоскости, перпенди­кулярной к его оси (в плоскости ри­сунка).

Рассмотренные виды связи яв­ляются идеальными, или связями без трения.

4. При наличии трения между те­лом и поверхностью связь, кроме нормальной реакции, дает еще до­полнительную реакцию - силу тре­ния F_тр. Сила трения всегда направ­лена в сторону, противоположную возможному перемещению тела по поверхности (рис. 7). Если тело, на которое действуют силы, покоится, то сила трения покоя всякий раз имеет то значение, которое необходимо для предотвращения скольжения. Мак­симальная величина силы трения по­коя определяется, как известно, из условия F_{тр max}= N, где  - коэффициент трения, а N - си­ла нормальной реакции поверхности. Таким образом, в зависимости от дру­гих сил, действующих на тело, сила трения покоя может принимать все значения от нуля до F_{тр max}. Подробнее о силах трения будет идти речь в следующих номерах журнала МИФ-2.

1.5. Основные задачи статики

В статике твердого тела рассмат­риваются две основные задачи:

1. Определение условий, при ко­торых тело под действием сил может находиться в равновесии.

2. Нахождение действующих на тело сил (в большинстве случаев- реакций связей), когда тело заведо­мо находится в равновесии.

Мы ограничимся рассмотрением только таких систем, в которых все действующие на тело силы лежат в одной плоскости, - так называемых плоских систем сил.

Любое движение твердого тела можно представить как наложение двух видов движения - поступатель­ного и вращательного (вокруг неко­торой оси). Тело будет оставаться в состоянии покоя, если не будет при­чин, приводящих к возникновению поступательного движения или вра­щения.

При поступательном движении тела можно рассматривать движе­ние одной точки тела - его центра масс.

Если сумма сил, приложенных к телу, равна нулю, то центр масс будет сохранять свою скорость неиз­менной и, в частности, будет по­коиться, если он был в покое. Но это еще не означает, что тело будет находиться в равновесии.

Р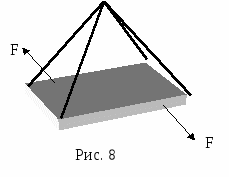ассмотрим следующую ситуацию. К бруску, лежащему на гладкой горизонтальной плоскости, в двух его точках приложены две силы, рав­ные по абсолютной величине и на­правленные в противоположные сторо­ны. (Такая система сил назы­вается парой сил.) Относительно ка­кой точки будет поворачиваться брусок?

О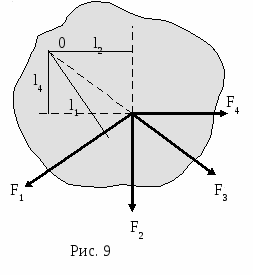пыт подсказы­вает, что брусок будет поворачи­ваться. Но так как сумма сил, дей­ствующих на тело, равна нулю, то центр масс его будет оставаться в покое, а пара сил вызовет вращение бруска вокруг оси, проходящей че­рез центр масс и перпендикулярной к плоскости, в которой лежат силы (рис. 8).

В общем случае; когда сумма сил, приложенных к телу, равна нулю (F_i = 0), а линии, вдоль которых действуют силы, не пересекаются в одной точке, центр масс сохраняет состояние движения неизменным, в частности, покоится, но само тело будет поворачиваться вокруг оси, проходящей через центр масс.

Итак, общие условия равно­весия для плоской системы сил:

Для равновесия тела необходимо и достаточно, чтобы были одновре­менно равны нулю векторная сумма приложенных к телу сил и алгебраи­ческая сумма моментов этих сил от­носительно любой точки О плоскости: F_i = 0 ;  М₀ (F_i) = 0 (рис. 9)

Для тела, способного вращаться вокруг закрепленной оси, единствен­ным условием равновесия будет ра­венство нулю алгебраической суммы моментов приложенных к нему сил относительно этой оси. Это правило называется правилом моментов.

Приступая к разбору следующих задач, укажем некоторые дополни­тельные легко доказуемые положения, которыми мы будем пользоваться.

1. Силу, приложенную к твердому телу, можно переносить по линии ее действия, при этом не изменяется ее момент относительно точки или оси.

2. Если на тело действует система сил, линии действия которых пере­секаются в одной точке, то мы можем перенести силы вдоль линий их дей­ствия в точку пересечения и сложить их, пользуясь правилом параллело­грамма. Если равнодействующая сила будет равна нулю и начальная ско­рость тела также равна нулю, то тело будет находиться в покое.

3. Если на тело действуют три не­параллельные силы, лежащие в одной плоскости, и под действием этих сил тело находится в равновесии, то ли­нии действия этих сил пересекаются в одной точке (это положение носит название теоремы о трех силах).

Примеры решения задач

З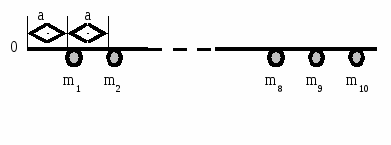адача 1. На невесомом стержне, разделен­ном на 10 равных частей, нанизаны десять шариков, массы которых рав­ны последовательно 1, 2, 3, ... , 9, 10 так, что их центры совпадают с точками делений. Опреде­лить, в каком месте должен опираться стержень на опору, чтобы находиться в равновесии.

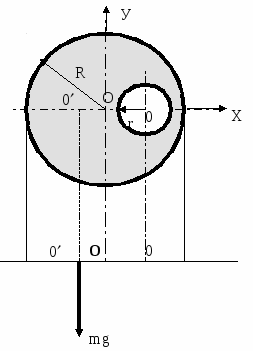Решение. Для выполнения условия F_i = 0 равновесия стержня не­обходимо, чтобы в точке опоры на стержень действовала сила реакции опоры, направленная вверх и равная по абсолютной величине R =  F = m_ig = 0,055 g (Н).

Чтобы выполнялось условие  М₀ (F_i) =0 рав­новесия, точка опоры должна нахо­диться на таком расстоянии х от точки 0 стержня, чтобы m_igх_i - Rx = 0, где х - расстояние от точки 0 до шарика с массой m_i:

(am₁g) + (2am₂g) + (3am₃g) +… + (10am₁₀g) = Rx.

Из этих равенств находим , то есть точка опоры совпадает с цент­ром шарика массы m₇. Рассмотренная задача по сущест­ву есть задача на определение центра тяжести для случая линейного распо­ложения точечных масс.

Задача 2. Найти центр тяжести круглой одно­родной пластины радиуса R с круг­лым вырезом радиуса r, центр кото­рого находится на середине радиуса R.

Решение. 1 способ. Центр масс данной системы лежит на оси Х (в силу симметрии). Поэтому рассчитать нужно только х_С. Положение центра масс (центра тяжести) можно найти по формуле , где m_i - масса всей системы. В данной задаче рассматриваются 2 тела – большой круг (его массу мы берем со знаком +) и малый круг (его массу мы берем со знаком « - », так как она отсутствует. В системе координат ХУ х_С =. Здесь m₁=; m₂ = -; х₁ = 0; х₂ = . Подставив эти значения в формулу для расчета х_С, получим - центр тяжести пластины нахо­дится слева от точки 0 на расстоянииот нее.

2 способ вычисления положения центра масс.

Найти центр масс (центр тяжести) однородного тела часто помогают соображения симметрии. Если тело имеет пло­скость, ось или центр симметрии, то центр тяжести лежит соответственно в плоскости, на оси или в центре симметрии. Так, центр тяжести одно­родного круглого кольца, круглого диска, тонкого стержня, прямоуголь­ной пластины, шара находится в их центре симметрии

В силу симметрии центр тяжести пластины лежит на линии, проходящей через центры большого (0) и маленького (o) кру­гов. Пусть он находится в точке 0 на расстоянии х от центра большого круга. «Дополним» фигуру до сплошного однородного круга. Центр тяжести при этом пере­местится в точку 0. 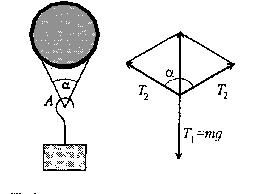Следовательно, сумма моментов сил тяжести перво­начальной фигуры и сплошного кру­га радиуса r относительно точки 0 равна нулю; , где  - плотность материала пластины. Отсюда - тот же самый результат.

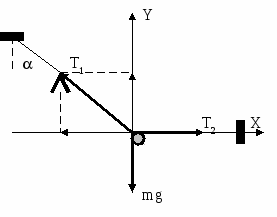Задача 3. На перекладину с круглым сечением надета петля из тон­кой легкой однородной нити. К петле с помощью не­весомого крюка А на такой же нити подвешен груз, массу ко­торого постепенно увеличивают до разрыва нити. Определи­те, при каких значениях угла α порвется петля, а при каких — нить, соединяющая груз с крюком.

Решение. Если выше и ниже крюка натяжения одинаковы, то 2Tcos(α/2)=T и α=120⁰. Значит, при 120⁰ нить может порваться в любом месте. Если α<120⁰ то Т₂<Т₁, поэтому нить порвется ниже крюка. Соответственно, если α>120⁰, то нить порвется выше крюка.

Задача 4. Груз массы m подвешен с по­мощью двух нитей так, что одна нить образует с вертикалью угол , a другая проходит горизонтально. Найти силы натяжения нитей.

Решение. На тело действуют сила тяжести mg и силы T₁ и Т₂ натяжения нитей (жирным шрифтом обозначим векторные величины). Спроектируем эти силы на оси координат Х и Yи запишем условия равновесия :

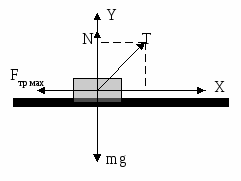по оси Х: Т₂ - T₁ sin  = 0;

по оси Y: T₁ Cos  - mg =0.

Решая эту систему уравнений, получаем

; .

Задача 5. Груз массы т перемещают с по­стоянной скоростью по горизонталь­ной плоскости с помощью троса. Коэффициент трения о плоскость ра­вен .

а) Найти силу Т натяжения троса, если он направлен под углом  к горизонту.

б) При каком угле  сила натяже­ния троса будет наименьшей? Чему она будет равна? Груз считать материальной точ­кой.

Решение. а) На груз дейст­вуют сила тяжести mg, сила N нормальной реакции плоскости, сила натяжения троса Т, максимальная сила трения F_тр._max (так как имеет место скольжение). Запишем усло­вия равновесия груза:

по оси Х: T Cos - F_тр._max= 0; по оси У: Tsin +N-mg = 0, N= mg - Tsin ;

F_тр._max= N = ( mg -Tsin ). Тогда Т.

Примечание. При решении этой задачи учащиеся допускают ошибку, считая

F_тр._max =mg.

б) Cила Т бу­дет минимальной, когда величина знаменателя (сos  +  sin ) мак­симальна. Обозначив  через tg , можно знаменатель преобразовать так:

cos  + tg sin =. Это выражение максимально при ( -  )= 0, откуда  =  = arc tg . Учитывая, что sin и , полу­чим .

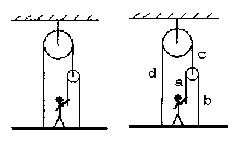Задача 6. С какой силой человек должен тянуть веревку, чтобы удержать платформу, на которой он стоит, если масса человека 60 кг, а масса платформы 20 кг?

Решение. Обозначим через F_a натяжение веревки на участке а, через F_b - на участке b и так далее. Тогда F_a = F_b = F и F_c = F_d = 2F. Условие равновесия: g(M + m) = F_a + F_b + F_d = 4F; F == 200 H

В задачах этого раздела исследуют условия равновесия тел. Обычно эти условия используют для нахождения сил в исследуемой системе.

Напомним условия равновесия те­ла: сумма сил, действующих на тело со стороны других тел, должна быть равна нулю и сумма моментов этих сил относительно любой точки тоже должна быть нулевой.

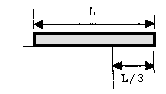Тут сразу может возникнуть вопрос: не получим ли мы сколько угодно уравнений, приравнивая нулю суммы моментов сил относительно разных точек, т. е. не получится ли урав­нений больше, чем неизвестных? Ока­зывается, оснований для беспокойства нет - у системы сил, сумма которых равна нулю (а мы имеем дело как раз с такими) суммарный момент одинаков относительно любой точки, так что «лишних» уравнений не будет.

Задача 7. Однородная доска массой М = 1 кг лежит на столе так, как показано на рисунке. Груз какой массы надо положить на правый конец, чтобы левый конец стал подниматься?

Решение. Из условия равенства моментов сил ; = 0,5кг.

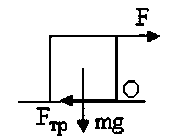Задача 8. Какое минимальное значение должен иметь коэффициент трения материала кубика, лежащего на шероховатой поверхности, чтобы его можно было опрокинуть через ребро горизонтально направленной силой, приложенной к его верхней грани. Чему равна эта сила, если масса кубика m.
Решение. Пусть длина ребра куба равна а, тогда условия равновесия имеют вид: Fa - mg = 0; F_тр – μmg = 0.
Значение минимальной силы, способной опрокинуть кубик,

F = = ; а так как F = F_тр , μ = 0,5.

Задача 9. Прямая балка длиной L= l м и массой М=200 кг подвешена за концы на вертикально натянутых тросах (рис.1). Найдите их натяже­ния, если центр тяжести балки нахо­дится на расстоянии L₁= 0,3 м от одно­го из ее концов.

Решение. Ясно, что если тросы целы, то балка находится в равновесии. Запишем уравнение для сил: Т₁+ Т₂ –Mg= 0. (1)

Неизвестных величин две – Т₁ и Т₂. Значит, нужно еще одно уравнение. Его мы получим, записав уравнение для моментов сил. Моменты можно брать относительно любой точки - выберем эту точку так, чтобы упро­стить решение системы уравнений.

Удобно взять ее на продолжении ли­нии действия одной (а если получит­ся, то и нескольких) из неизвестных сил. В нашем случае можно взять один из концов балки - например, левый: МgL₁ – Т₁L = 0. (2)

Решая систему уравнений (1) и (2), получим

T₁ = Mg(L - L₁)/L = 1,4·10³ Н,

T₂ = MgL₁/L = 0,6 ·10³ Н.

Обратите внимание: вместо уравнения (1.) можно было взять уравнение мо­ментов относительно другого конца балки, тогда ответы можно было бы записать сразу. Попробуйте сами обосновать возможность такого выбо­ра уравнений.

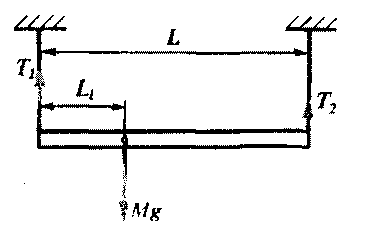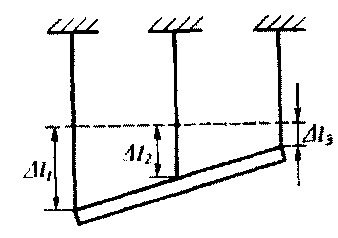И еще одно замечание: если тросы растянулись совсем немного, то балка практически останется горизонтальной, и, значит, наше решение оста­нется в силе. Раз так, то мы вообще вправе пренебрегать растяжением тро­сов (т. е, можно считать их нерастя­жимыми).

Задача 10. Балка висит не на двух, а на трех тросах - третий трос дер­жит балку посередине. Тросы нареза­ны из одного куска, в нерастянутом состоянии тросы были одинаковой длины. Найдите силы натяжения тро­сов. Указание: растяжения тросов малы и для упрощения расчетов тро­сы можно считать вертикальными. Де­формациями балки пренебречь.

Решение. Нарисуем чертеж условно, сильно увеличив для наглядности де­формации тросов. Из геометрических соображений ; Δl₂ = (Δl1+ Δl₃).

Уравнения сил и моментов: Т₁+T₂+Т₃ = Мg, MgL₁- Т - T₃L = 0.

Считая деформации упругими, запи­шем: T₁: T₂ : T₃ = Δl₁: Δl₂ : Δl₃. Последнее уравнение дополняет ус­ловия равновесия, которых явно недо­статочно для решения этой задачи (такие системы называют статически не определенными, имея в виду необ­ходимость дополнительных уравне­ний).

Теперь получилась система: Т₁+T₂+Т₃ = Мg,

T₂ + 2T₃ = 2Мg,

2T₂ = Т₁+ Т₃.

Решив ее, находим T₁ = Mg( - ) = Mg, T₂ = Мg, T₃ = Mg( - ) = Мg.

Если тросы нерастяжимы, то до­статочно взять средний чуть длин­нее - и вся нагрузка ляжет на край­ние, а если будет чуть короче, исчез­нет нагрузка на правый трос. Понят­но, что в этой задаче пренебречь растя­жимостью тросов нельзя. Но даже ес­ли бы мы забыли об этом, задача сама напомнила бы нам - нехваткой уравнений.
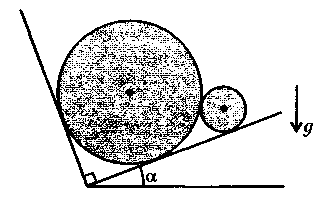Задача 11. Цилиндр радиусом R и массой М соприкасается с дном и боковой стенкой наклонной прямоугольной коробки (рис.). Второй цилиндр меньшего радиуса r и массой m соприкасается с первым цилиндром и дном коробки. Найдите отношение масс М/m, если при угле наклона дна с горизонталью α первый цилиндр начи­нает подниматься. Трение между цилиндрами, стенкой и дном коробки отсутствует.

Решение. Сила нормального давления N одного цилиндра на другой образует угол β с дном коробки такой, что sin β = (R - r)/(R + r). Из равновесия правого цилиндра име­ем mg sin α = N cos β (проекции сил вдоль дна коробки ). Для левого цилиндра (проекции сил вдоль стенки) получаем

Mg cos α = N sin β. Отсюда находим tgαtgβ =.

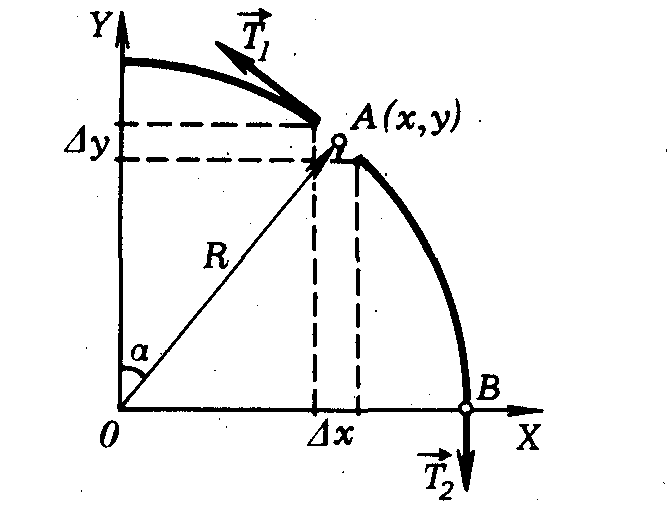Задача 12. На гладком блоке радиусом R висит однородный гибкий канат массой m и длиной l. Определить максимальную силу натяжения каната.

Решение. Рассмотрим кусочек каната длиной Δl, находящийся в точке А с координатами (х, у). Момент силы тяжести относительно точки 0 равен

ΔM = g Δl·x = g Δl R sinα =gR Δy.

Следовательно, момент силы тя­жести куска каната АВ относительно точки 0 равен М_AB=gR·y и условие его равновесия имеет вид T₁R = T₂R+M_AB = T₂R +gyR, где T₁ и T₂ - натяжение каната в точках А и В соответственно. Из последнего равенства видно, что T_{1 max}= T₂+ gR. Так как 2Т₂= g(l - πR), то T_{1 max}=

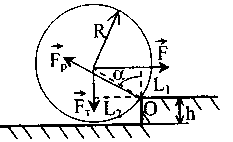Задача. 13. Тяжелый цилиндрический каток необходимо поднять на ступеньку высоты h. Определить наименьшую силу F_мин, которую необходимо приложить к центру катка в горизонтальном направлении, если каток имеет радиус R, а сила тяжести равна F_т.

Решение. На каток действуют силы: Fт = mg – сила тяжести, F_p – реакция опоры (учтите, что эта сила направлена не точно на центр катка для того, чтобы был некоторый момент, который придавал бы ему вращение); F – прилагаемое усилие.

Условие равновесия катка относительно точки О имеет вид: M₁ = M₂; FL₁= F_тL₂; (момент силы реакции опоры F относительно точки О равен 0). Здесь L₁= Rcos α; L₂ = Rsinα. Отсюда F = F_тtgα = mgtgα.

Видно, что, чтобы поднять каток на ступеньку, необходимо приложить силу F = F_т·tg α₀, где α₀ - угол в момент отрыва. tg α₀ = , тогда F_мин= F_т.

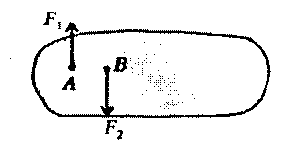Задание 5. Задачи-вопросы. (Каждый ответ оценивается 2 баллами)

1. При перемещении тела с экватора на полюс действующая на него сила тяжести меняется. Отражается ли это на положении центра тяжести тела?

2. Можно ли найти центр тяжести «гантели», состоящей из двух массив­ных шариков, соединенных невесо­мым стержнем, при условии, что дли­на «гантели» сравнима с диаметром Земли?

3. 
   Почему при резком торможении автомобиля его передняя часть опус­кается?
   

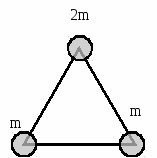4. Однородное тело находится в покое. К точкам А и В приложили две равные и противоположно направлен­ные силы, как показано на рисунке. В каком направлении станет двигаться точка В?

5. Где находится центр тяжести буб­лика?

6. В цилиндрический стакан понем­ногу наливают воду. Как будет изме­няться положение центра тяжести си­стемы стакан - вода?

7. Какой длины конец надо отрезать от однородного стержня, чтобы его центр тяжести сместился на Δl ?

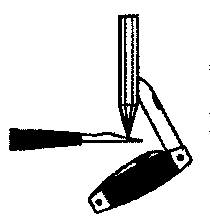8. Однородный стержень согну­ли посередине под прямым углом. Где оказался теперь его центр тяжес­ти?

9. Найдите центр тяжести системы шаров, находящихся в вершинах равностороннего невесомого треугольни­ка, изображенного на рисунке.

10. Невысокий деревянный ци­линдр, обточенный с одного конца в форме полушара, остается в покое, если его поставить на горизонталь­ную плоскость любой точкой закруг­ления. Где находится его центр тяже­сти?

11. Почему трудно передвигаться на ходулях?

12. Когда канатоходцу легче удер­жать равновесие - при обычном пере­движении по канату или при переносе сильно изогнутого коромысла, нагру­женного ведрами с водой?

13. Как объяснить сохранение рав­новесия в случае, показанном на ри­сунке?

Задание 6. Расчетные задачи (Решение каждой задачи оценивается 5 баллами)

1. На невесомом стержне, разделен­ном на 5 равных частей, нанизаны десять шариков, массы которых рав­ны последовательно 1, 2, 3, 4, 5 так, что их центры совпадают с точками делений. Опреде­лить, в каком месте должен опираться стержень на опору, чтобы находиться в равновесии.

2. Три однородных шара ничтожно малого радиуса массами 100 г, 200 г и 300 г крепятся на невесомом стержне на расстоянии 30 см друг от друга. На каком расстоянии от центра третьего шара находится центр тяжести системы?

3. На правом конце стержня длиной 30 см прикреплен шар радиусом 6 см. Определить положение центра тяжести системы относительно левого конца стержня, если масса стержня вдвое меньше массы шара.

4. Стержень состоит наполовину длины из материала с плотностью 8100 кг/м³, наполовину из алюминия с плотностью 2700 кг/м³. Определить местоположение центра тяжести стержня относительно его геометрического центра, если вся длина его 80 см, а сечение по всей длине одинаково.

5. Груз массы 10 кг подвешен с по­мощью двух нитей так, что одна нить образует с вертикалью угол 30^о, a другая проходит горизонтально. Найти силы натяжения нитей.

6. На перекладине висит груз массой 600 кг на расстоянии 1/3 длины от одного из концов. Короткий конец перекладины поддерживается тросом, длин­ный лежит на опоре. Определить силу натяжения троса.

7. На гладком блоке радиусом 10 см висит однородный гибкий канат массой 12 кг и длиной 5 м. Определить максимальную силу натяжения каната.

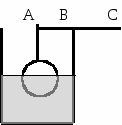8. К концу однородной палочки массой 4,4 г подвешен на нити алюминиевый шарик радиуса 0,5 см. Палочку кладут на край стакана с водой так, что половина объема шарика оказывается в воде. Определить отношение плеч ВС к АВ, при котором палочка будет находиться в равновесии.

9. На шероховатом полу лежит деревянный ящик в форме куба. Какое минимальное значение должен иметь коэффициент трения между ящиком и полом, чтобы его можно было опрокинуть через ребро горизонтально направленной силой, приложенной к середине его верхней грани. Чему равна эта сила, если масса ящика 20 кг?

10. Длинная однородная деревянная доска плавает в воде, погрузившись в нее наполовину своего объема. На один конец доски положили груз, в результате чего этот конец опустился в воду до своего верхнего ребра. Какая часть объема доски в этом случае будет погружена в воду? Ответ выразить с точностью до тысячных.