практическое занятие по информатике. ЗЖУ 1912. Фон Неймана 2
 Скачать 112.3 Kb. Скачать 112.3 Kb.
|
Содержание Принцип фон Неймана 2 Введение 2 Как работает машина фон Неймана 3 Формула Хартли 6 Формула Шеннона 8 Единицы международной системы единиц (СИ) 9 Принцип фон Неймана ВведениеВ 1946 году Д. фон Нейман, Г. Голдстайн и А. Беркс в своей совместной статье изложили новые принципы построения и функционирования ЭВМ. В последствие на основе этих принципов производились первые два поколения компьютеров. В более поздних поколениях происходили некоторые изменения, хотя принципы Неймана актуальны и сегодня. По сути, Нейману удалось обобщить научные разработки и открытия многих других ученых и сформулировать на их основе принципиально новое. Принципы фон Неймана: Использование двоичной системы счисления в вычислительных машинах. Преимущество перед десятичной системой счисления заключается в том, что устройства можно делать достаточно простыми, арифметические и логические операции в двоичной системе счисления также выполняются достаточно просто. Программное управление ЭВМ. Работа ЭВМ контролируется программой, состоящей из набора команд. Команды выполняются последовательно друг за другом. Созданием машины с хранимой в памяти программой было положено начало тому, что мы сегодня называем программированием. Память компьютера используется не только для хранения данных, но и программ. При этом и команды программы и данные кодируются в двоичной системе счисления, т.е. их способ записи одинаков. Поэтому в определенных ситуациях над командами можно выполнять те же действия, что и над данными. Ячейки памяти ЭВМ имеют адреса, которые последовательно пронумерованы. В любой момент можно обратиться к любой ячейке памяти по ее адресу. Этот принцип открыл возможность использовать переменные в программировании. Возможность условного перехода в процессе выполнения программы. Не смотря на то, что команды выполняются последовательно, в программах можно реализовать возможность перехода к любому участку кода. Самым главным следствием этих принципов можно назвать то, что теперь программа уже не была постоянной частью машины (как например, у калькулятора). Программу стало возможно легко изменить. А вот аппаратура, конечно же, остается неизменной, и очень простой. Для сравнения, программа компьютера ENIAC (где не было хранимой в памяти программы) определялась специальными перемычками на панели. Чтобы перепрограммировать машину (установить перемычки по- другому) мог потребоваться далеко не один день. И хотя программы для современных компьютеров могут писаться годы, однако они работают на миллионах компьютерах после несколько минутной установки на жесткий диск. Как работает машина фон Неймана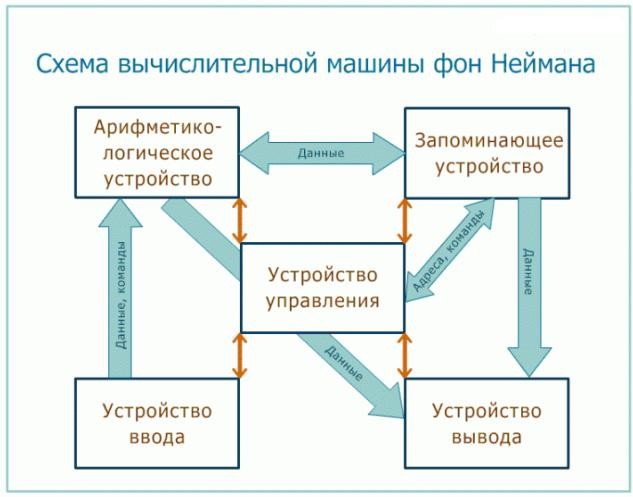 Рисунок1МашинафонНеймана Машина фон Неймана (Рисунок 1 Машина фон Неймана) состоит из запоминающего устройства (памяти) - ЗУ, арифметико-логического устройства - АЛУ, устройства управления – УУ, а также устройств ввода и вывода. Программы и данные вводятся в память из устройства ввода через арифметико-логическое устройство. Все команды программы записываются в соседние ячейки памяти, а данные для обработки могут содержаться в произвольных ячейках. У любой программы последняя команда должна быть командой завершения работы. Команда состоит из указания, какую операцию следует выполнить (из возможных операций на данном «железе») и адресов ячеек памяти, где хранятся данные, над которыми следует выполнить указанную операцию, а также адреса ячейки, куда следует записать результат (если его требуется сохранить в ЗУ). Арифметико-логическое устройство выполняет указанные командами операции над указанными данными. Из арифметико-логического устройства результаты выводятся в память или устройство вывода. Принципиальное различие между ЗУ и устройством вывода заключается в том, что в ЗУ данные хранятся в виде, удобном для обработки компьютером, а на устройства вывода (принтер, монитор и др.) поступают так, как удобно человеку. УУ управляет всеми частями компьютера. От управляющего устройства на другие устройства поступают сигналы «что делать», а от других устройств УУ получает информацию об их состоянии. Управляющее устройство содержит специальный регистр (ячейку), который называется «счетчик команд». После загрузки программы и данных в память в счетчик команд записывается адрес первой команды программы. УУ считывает из памяти содержимое ячейки памяти, адрес которой находится в счетчике команд, и помещает его в специальное устройство — «Регистр команд». УУ определяет операцию команды, «отмечает» в памяти данные, адреса которых указаны в команде, и контролирует выполнение команды. Операцию выполняет АЛУ или аппаратные средства компьютера. В результате выполнения любой команды счетчик команд изменяется на единицу и, следовательно, указывает на следующую команду программы. Формула ХартлиДопустим, нам требуется что-либо найти или определить в той или иной системе. Есть такой способ поиска как «деление пополам». Например, кто-то загадывает число от 1 до 100, а другой должен отгадать его, получая лишь ответы «да» или «нет». Задается вопрос: число меньше? Ответ и «да» и «нет» сократит область поиска вдвое. Далее по той же схеме диапазон снова делится пополам. В конечном итоге, загаданное число будет найдено. Посчитаем сколько вопросов надо задать, чтобы найти задуманное число. Допустим загаданное число 27. Начали: Больше 50? Нет Больше 25? Да Больше 38? Нет Меньше 32? Да Меньше 29? Да Больше 27? Нет Это число 26? Нет Ура! если число не 26 и не больше 27, то это явно 27. Чтобы угадать методом «деления пополам» число от 1 до 100 нам потребовалось 7 вопросов. Кто-то может задаться вопросом: а почему именно так надо задавать вопросы? Ведь, например, можно просто спрашивать: это число 1? Это число 2? И т.д. Но тогда вам потребуется намного больше вопросов (возможность того, что вы телепат, и угадаете с первого раза не рассматривается). «Деление пополам» самый короткий рациональный способ найти число. Объем информации заложенный в ответ «да» или «нет» равен одному биту. Действительно, ведь бит может быть в состоянии 1 или 0. Итак, для угадывания числа от 1 до 100 нам потребовалось семь бит (семь ответов «да» - «нет»). 𝑁 = 2𝑘 Такой формулой можно представить, сколько вопросов (бит информации) потребуется, чтобы определить одно из возможных значений. N – это количество значений, а k – количество бит. Например, в нашем примере 100 меньше чем 27, однако больше, чем 26. Да, нам могло потребоваться и всего 6 вопросов, если бы загаданное число было бы 28. Формула Хартли: 𝑘 = log2 𝑁. Количество информации (k), необходимой для определения конкретного элемента, есть логарифм по основанию 2 общего количества элементов (N). Формула ШеннонаВ случае, когда вероятность элементов не одинакова, для определения количества информации, достаточной для выявления элемента, используют формулу Шеннона. Ее можно получить из формулы Хартли. 𝑘 = 𝑁 (формула Хартли) 𝑁 – вероятность каждого исхода, если все они равновероятны. − 𝑁2𝑁 – вклад в k (общую неопределенность, количество информации) одного исхода. При неравновероятных исходах пусть вклад каждого обозначается буквой P с индексным номером: 1, 2, 3, 4 …. N. Получаем формулу: 𝑘 = −𝑃1 log2 𝑃1 - 𝑃2 log2 𝑃2 - 𝑃3 log2 𝑃3 - … - 𝑃𝑁 log2 𝑃𝑁 Чем больше k, тем больше информации содержится в системе. Максимальное значение k имеет лишь тогда, когда все исходы равновероятны. Единицы международной системы единиц (СИ)В следующей таблице приведены примеры производных единиц СИ, наименования и обозначения которых образованы с использованием наименований и обозначений основных единиц СИ.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
