Формальные языки и грамматики

• Название: Формальные языки и грамматики
• Дата: 16.10.2020
• Размер: 174 Kb.
• Имя файла: (3);(4.....);(5);(20....).doc
• Тип: Задача; #143411

Министерство образования и науки Украины

Севастопольский национальный технический университет

Кафедра кибернетики

и вычислительной техники

Расчетное задание №3

по дисциплине

«Алгоритмы и формальные преобразования»:

«Формальные языки и грамматики»

Выполнила

студентка группы М- 21д

Дятлова Е. А.

вариант 16

Проверила

Иванова Л. В.
Севастополь

2004

1. 
   Задача №1
   
   1. 
      Постановка задачи
      

К какому типу по Хомскому относится данная грамматика? Какой язык она порождает? Каков тип языка?
a) S  APA b) S  aQb | e

P  + | - Q  cSc

A  a | b
c) S  1B d) S  A | SA | SB

B  B0 | 1 A  a

B  b

2. 
   Решение
   

а) Это грамматика типа 1, так как она является неукорачивающей. и S  APA где и

Грамматика порождает язык вида - это язык 3 типа когда
б) Это грамматика 2 типа, то есть контекстно-свободная, так как

и S  aQb | e , где ,

Грамматика порождает язык вида - это язык 3 типа.
в) Это грамматика 3 типа, то есть регулярная, так как

и B  B0 | 1 , где ,

Грамматика порождает язык вида - это язык 0 типа когда
г) Это грамматика 2 типа (контекстно-свободная), когда S  A | SA | SB , где ,

Грамматика порождает язык 3 типа, когда
2. Задача №2

2.1 Постановка задачи

4. 
   Построить грамматику, порождающую язык:
   

1. 
   L = { aⁿ b^m | n, m >= 1}
   
2. 
   L = { acbcgc | a, b, g - любые цепочки из a и b}
   
3. 
   L = { a₁ a₂ ... a_n a_n ... a₂ a₁ | a_i = 0 или 1, n >= 1}
   
4. 
   L = { aⁿ b^m | n ¹ m ; n, m >= 0}
   
5. 
   L = { цепочки из 0 и 1 с неравным числом 0 и 1}
   
6. 
   L = { w | w Î {0,1}⁺ и содержит равное количество 0 и 1, причем любая подцепочка, взятая с левого конца, содержит единиц не меньше, чем нулей}.
   
7. 
   L = { | n >= 1}
   

2.2 Решение

а)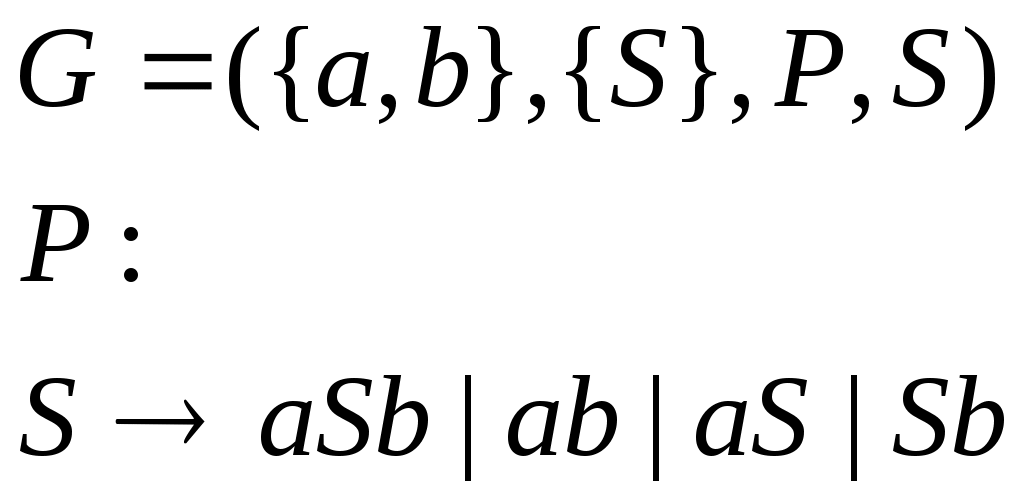



в)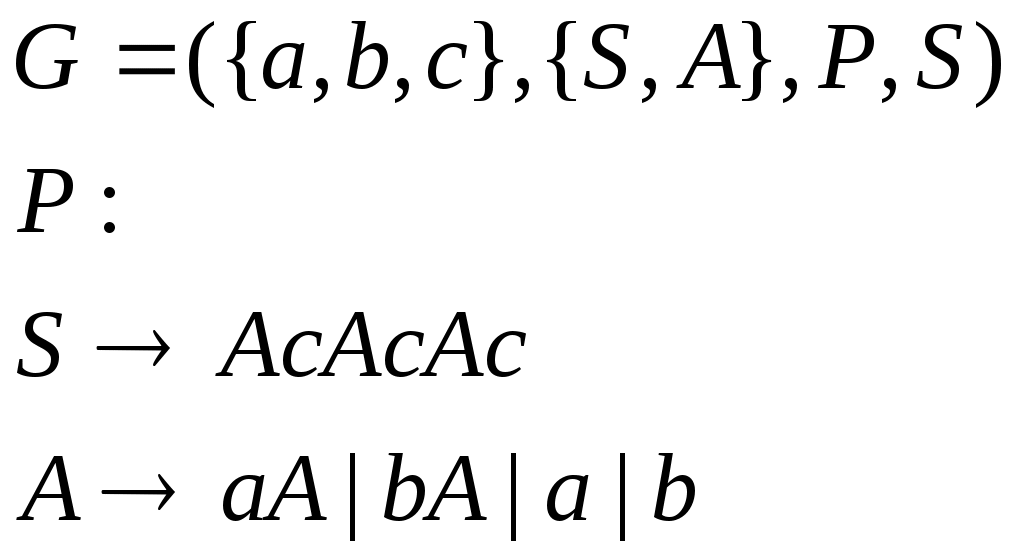



с)



д)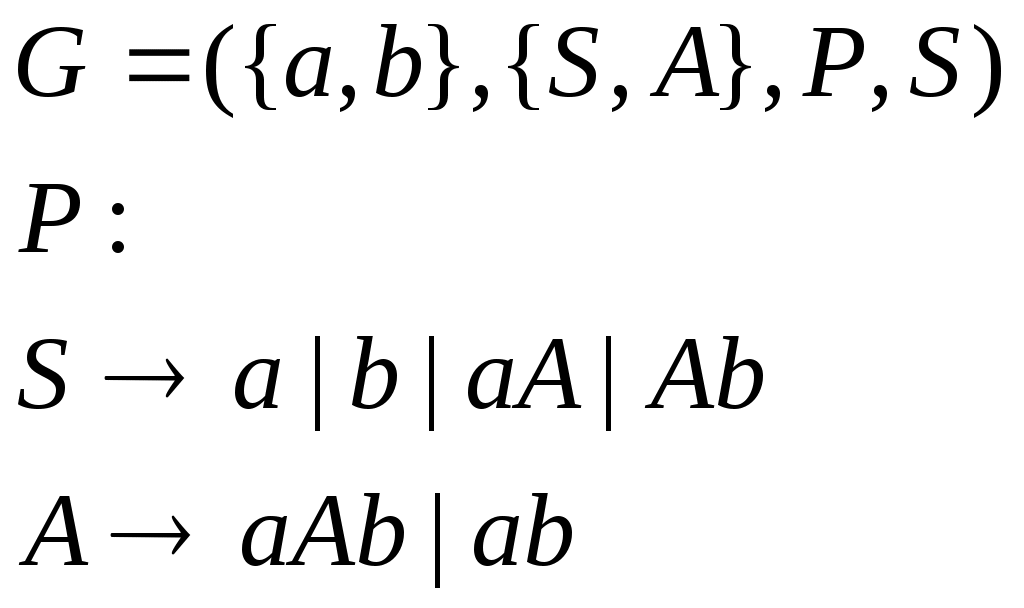



е)



f)



g)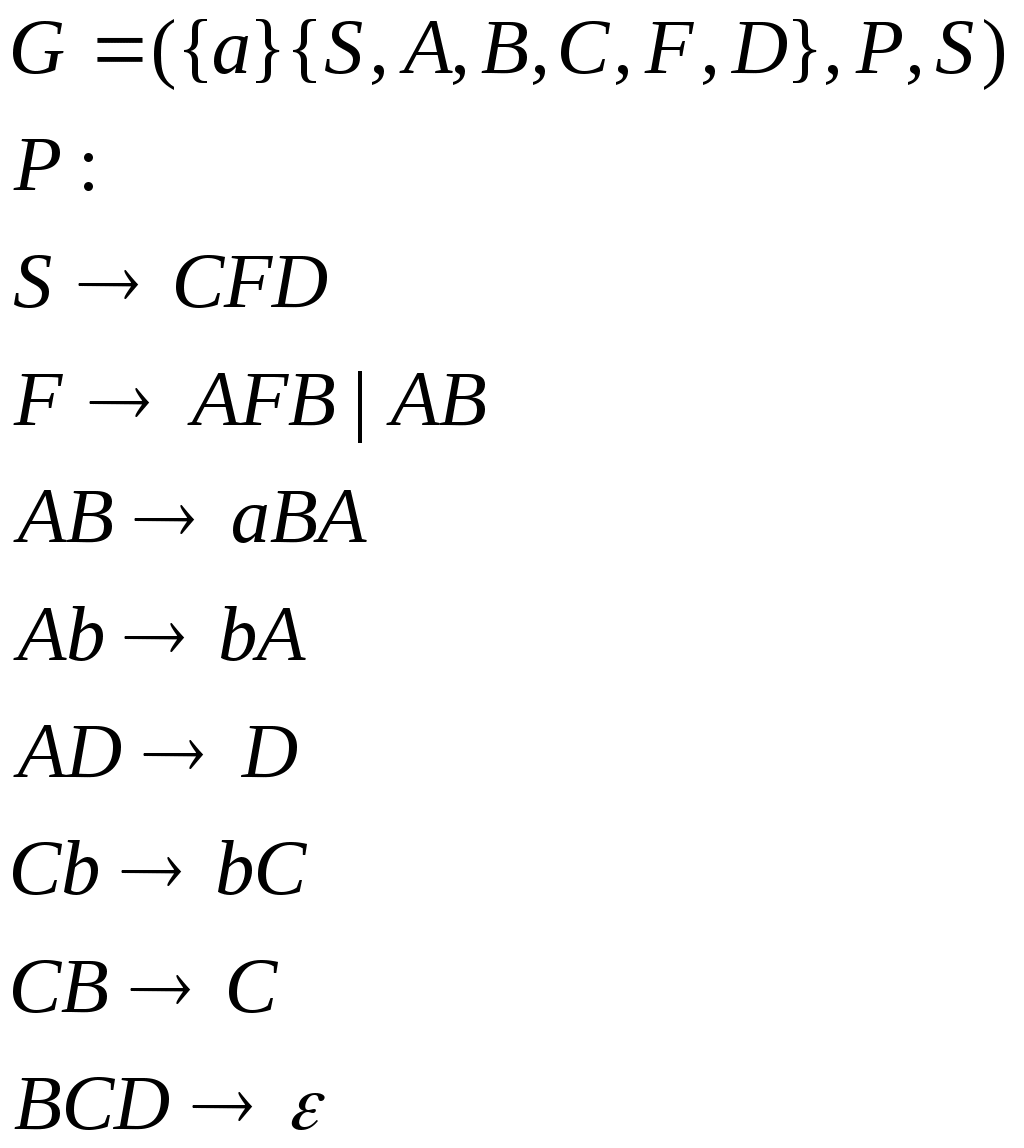

3. 
   Задача №3
   

3.1 Постановка задачи


К какому типу по Хомскому относится данная грамматика? Какой язык она порождает? Каков тип языка?
a) S  a | Ba b) S  Ab

B  Bb | b A  Aa | ba
c) S  0A1 | 01 d) S ® Ab | c

0A  00A1 A ® Ba

A  01 B ® cS

*e) S  A | B *f) S  0A | 1S

A ® aAb | 0 A ® 0A | 1B

B ® aBbb | 1 B ® 0B | 1B | ^
*g) S ® 0S | S0 | D *h) S ® 0A | 1S | e

D ® DD | 1A | e A ® 1A | 0B

A ® 0B | e B ® 0S | 1B

B ® 0A | 0
*i) S ® SS | A *j) S ® AB^

A ® a | bb A ® a | cA

B ® bA


3.2 Решение

a) Это грамматика типа 3, когда B  Bb | b , где ,

Порождаемый язык - Тип языка -3

2. 
   Это грамматика типа 2 (контекстно-свободная), так как все правила имеют вид , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 1 (контекстно-зависимая), так как некоторые правила имеют вид , где ,
   

Порождаемый язык - . Тип языка - 1

2. 
   Это грамматика типа 3 , когда , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 2 (контекстно-свободная), так как все правила имеют вид , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 3 , когда , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 2 (контекстно-свободная), так как все правила имеют вид , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 2 (контекстно-свободная), так как все правила имеют вид , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 2 (контекстно-свободная), так как все правила имеют вид , где ,
   

Порождаемый язык - . Тип языка - 3

2. 
   Это грамматика типа 3 , когда , где ,
   

Порождаемый язык - . Тип языка - 3

3. 
   Задача №4
   

4.1 Постановка задачи

Написать КС-грамматику, порождающую язык L, и вывод для цепочки 110000111 в этой грамматике.
L = {1ⁿ 0^m 1^p | n+p>m; n, p, m>0}.
4.2 Решение

Грамматика, порождающая язык L:


Вывод, для цепочки 110000111:

3. 
   Задача№5
   

5.1 Постановка задачи

Написать общие алгоритмы построения по данным КС-грамматикам G1 и G2, порождающим языки L1 и L2, КС-грамматики для

1. 
   L1ÈL2
   
2. 
   L1 * L2
   
3. 
   L1^*
   

5.2 Решение

Грамматика языка L будет иметь вид

а) Для случая, когда для построения грамматики языка нужно:

1.

2.

3.

Если выполняются пункты 1-2, но пункт 3 нужно будет преобразовать, так чтобы не получилось недопустимых цепочек

б) Для построения грамматики языка нужн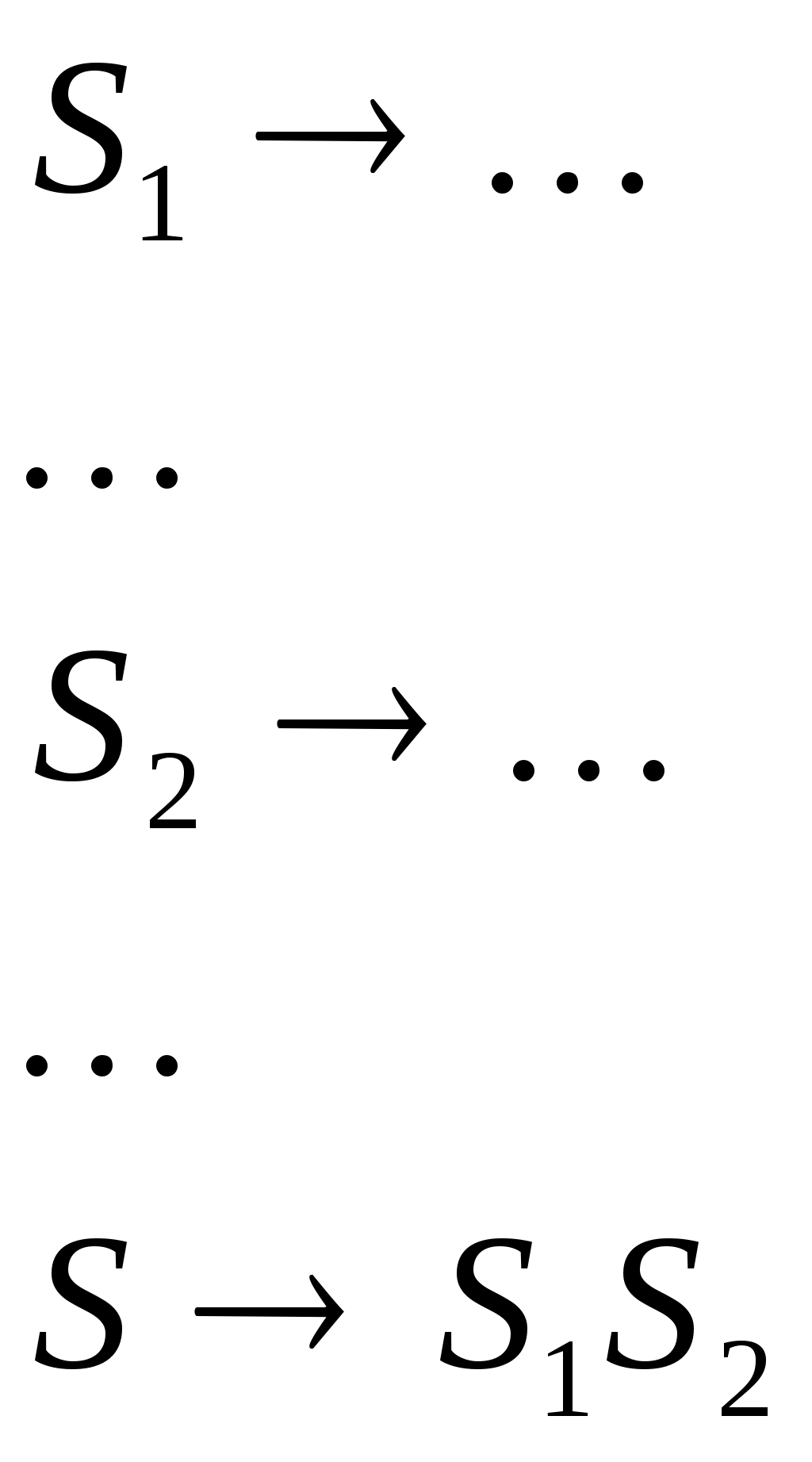о:

1.

2.

3 Р:



в) Для построения грамматики языка нужн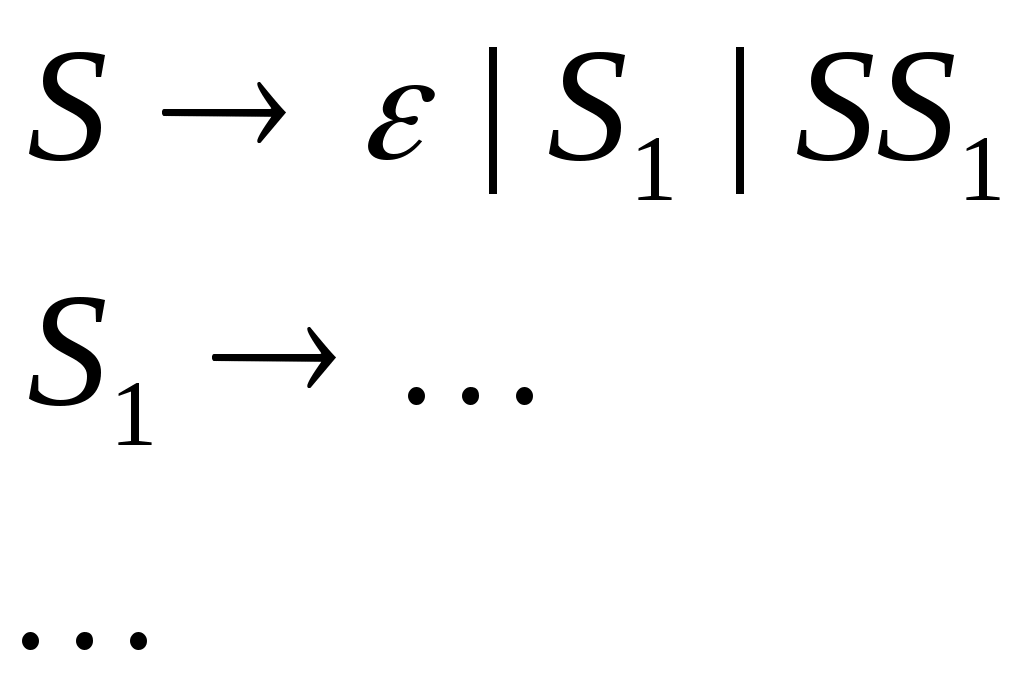о:

1.

2.

3 Р: