лб 1. Формирование выборки экспериментальных данных с заданными статистическими характеристиками
 Скачать 95.52 Kb. Скачать 95.52 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Школа: Инженерная школа ядерных технологий Направление: 01.04.02 Прикладная математика и информатика Профиль: Математическое моделирование и компьютерные вычисления Отчёт по лабораторной работе №1 «Формирование выборки экспериментальных данных с заданными статистическими характеристиками» Выполнил студент гр.0ВМ02 Захаров В.К. Проверил преподаватель: Кочегуров А. И. Томск – 2021 Задание 1. Сгенерировать последовательность x (n) в виде выборки случайных данных с нормальным законом распределения с помощью датчика случайных чисел (ДСЧ).Значения атематического ожидания и дисперсии выбрать из таблицы 1 в соответствии с вашим вариантом.Объем выборки 200 значений. 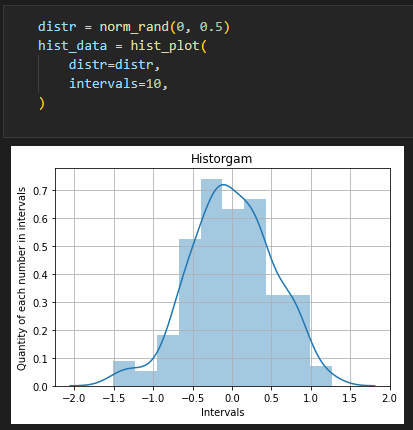 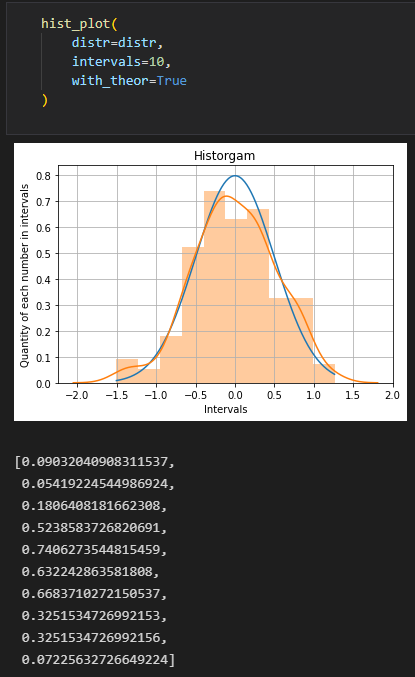 Получившееся распределение: [0.09032040908311537, 0.05419224544986924, 0.1806408181662308, 0.5238583726820691, 0.7406273544815459, 0.632242863581808, 0.6683710272150537, 0.3251534726992153, 0.3251534726992156, 0.07225632726649224]. Число степеней свободы 10 - 3 = 7, тогда полученная оценка критерия Пирсона: Найдем оценки математического ожидания и дисперсии и сравним их с заданными значениями. Проверим несмещенность и состоятельность полученных оценок. 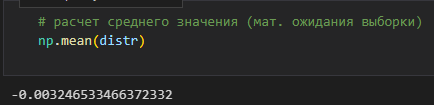 Полученное значение находится в окрестности теоретической (0), что подтверждает несмещенность полученной оценки. При увелении выборки, видно, что математическое ожидание стремится к 0, что подтверждает состоятельность оценки, такой же вывод можно по оценки дисперсии.  Вывод: Была сгенерированна последовательность из псевдослучайных величин, согласно заданным параметрам дисперсии и математического ожидания. Согласно оценке, дисперсия и мат. ожидание максимально сходится с заданными изначально. Для увеличения точности можно увеличить объем выборки. Дополнительные инструменты: # helping functools # function that returns normal distribution def norm_rand(mu: float, sigma: float) -> np.ndarray: return np.random.normal(mu, sigma, 200) # histograms def hist_plot(distr: Union[np.ndarray, List], intervals: int, with_theor=False) -> None: if with_theor: x, y = normal_dist(distr) plt.plot(x, y) plot = sns.distplot(distr, intervals) plt.xlabel("Intervals") plt.ylabel("Quantity of each number in intervals") plt.title("Historgam") plt.grid() plt.show() return [h.get_height() for h in plot.patches] # normal distribution def normal_dist(distribution: Union[np.ndarray, List]): x = np.linspace(min(distribution), max(distribution), 200) mean = 0 sd = 0.5 prob_density = 1 / (np.sqrt(2 * np.pi)*sd) * np.exp(-0.5*((x-mean)/sd)**2) return x, prob_density |
