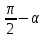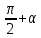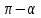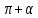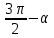10 класс 16.11.2020 1 урок. Формулы приведения
 Скачать 66.31 Kb. Скачать 66.31 Kb.
|
|
Формулы приведения - Это соотношения, с помощью которых значения тригонометрических функций аргументов и др., выражаются через значения sinα, cosα, tgα, ctgα. Тригонометрические тождества — математические выражения для тригонометрических функций, выполняющиеся при всех значениях аргумента (из общей области определения).  Рисунок 1. Знаки тригонометрических функций на окружности по координатным четвертям.
В формулах приведения есть такое понятие – «Кофункция» - это та же самая функция с добавлением или удалением приставки «КО». Например, для функции sin α (синус) кофункцией будет cos 𝛼 (КОсинус), а для функции КОсинуса будет синус (без КО) Если «точка привязки» 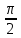 (90°) или (90°) или 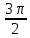 (270°), то функция меняется на кофункцию. (270°), то функция меняется на кофункцию.Если «Точка привязки» 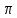 или или 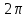 , то функция не меняется. , то функция не меняется. Пример. cos ( 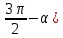 . Смотрим. . Смотрим. У нас здесь число 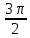 , а значит, функция меняется. Получается sin α. Осталось определить знак. Для этого рисуем Окружность и смотрим на ней, в какую сторону идём. , а значит, функция меняется. Получается sin α. Осталось определить знак. Для этого рисуем Окружность и смотрим на ней, в какую сторону идём.  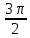 - это 270°. Для того, чтобы отнять - это 270°. Для того, чтобы отнять 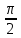 , нам нужно повернуть влево. В этой координатной четверти знак синуса отрицательный (смотри рисунок 1). , нам нужно повернуть влево. В этой координатной четверти знак синуса отрицательный (смотри рисунок 1).Рассмотрим еще один пример. cos ( 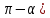 . Опять же. У нас здесь число π , а это значит, функция не меняется. Получается cos α. Осталось определить знак. Визуально представляем, что α = . Опять же. У нас здесь число π , а это значит, функция не меняется. Получается cos α. Осталось определить знак. Визуально представляем, что α = 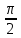 , тогда, чтоб отнять от числа π число , тогда, чтоб отнять от числа π число 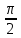 , на координатной окружности, линия перейдёт во вторую четверть. Здесь знак минус. , на координатной окружности, линия перейдёт во вторую четверть. Здесь знак минус. Ответ: - cos 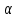   Вычислите следующие примеры: cos ( 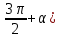 + sin ( + sin (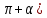 sin ( 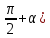 – cos( – cos(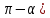 2sin( 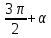 )+ sin( )+ sin(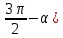 tg( 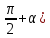 +2 tg( +2 tg(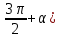 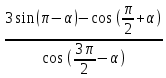 | |||||||||||||||||||||||||||||||||||||||||||||||