фракталы. проект фракталы. Фрактальная геометрия в природных объектах

• Название: Фрактальная геометрия в природных объектах
• Анкор: фракталы
• Дата: 14.04.2022
• Размер: 1.85 Mb.
• Имя файла: проект фракталы.docx
• Тип: Документы; #474894

Муниципальное автономное общеобразовательное учреждение

«Гимназия № 5» г. Альметьевска РТР

ПРОЕКТ

на тему «Фрактальная геометрия в природных объектах»

(Математика)

ученика 10А класса

Даминова Алишера Фаниловича

Руководитель проекта: учитель математики

Храмова Анжела Александровна

г. Альметьевск, 2022 г.

Оглавление

Введение 3

Глава 1. Теоретические аспекты фрактала. 4

Введение 3

Глава 1. Теоретические аспекты фрактала. 4

1.Понятие фрактала. История создания фрактала. 4

2.Классификация фракталов. 5

2.1Геометрические фракталы 5

2.2Алгебраические фракталы 7

4. 
   . Физические фракталы 8
   

Глава 2. Создание фрактального изображения 10

1. Описание создания фрактального изображения 10

2. Сравнение фрактального изображения с реальным………………………...12

Заключение ………………………………………………………………………15

Список литературы ……………………………………………………………...16

Введение

Природа Земли очень разнообразна, и может показаться, что она беспорядочна, хаотична, но если приглядеться, то можно увидеть характерные черты, присущие лепесткам цветка и даже извилистому течению реки. Она создаёт сложные по форме объекты (например, пористые облака, кроны деревьев и т.д.), которые достаточно сложно изобразить с помощью обычных геометрических фигур, например, треугольников, окружностей, прямых, сфер и т.д.

В мире вокруг нас присутствует геометрия. Эта геометрия выражается фракталами. Они приближают нас к пониманию некоторых процессов и явлений.

Актуальность проблемы: Фракталы находят своё применение в различных сферах деятельности: компьютерной графике; естественных науках; экономике. Они помогают изучить различные процессы и явления.

Чтобы изучить тему, нам нужно было решить следующую проблему: как построить фрактал, который будет идентичен реальному природному объекту?

Цель: Сравнить реальное изображение природного объекта с искусственно созданным фракталом.

Для достижения поставленной цели в работе решаются следующие задачи:

1) Изучить теоретические аспекты фрактала (понятие фрактала, его классификация)

2) Создать фрактальное изображение и описать алгоритма его построения.

3) Сравнить полученное изображение с реальным.

Гипотеза: Средства фрактальной графики позволяют создавать изображения, близкие к природным объектам.

Предполагается, что будет сгенерировано изображение искусственного фрактала, которое будет сравнено с реальным.

Глава 1. Теоретические аспекты фрактала.

1. Понятие фрактала. История создания фрактала.

Термины фрактал и фрактальная геометрия, появившиеся в конце 70-х, начали крепко входить в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Первые идеи фрактальной геометрии возникли в 19 веке, тогда и появился один из простейших фракталов – «Пыль Кантора» (рис. 1).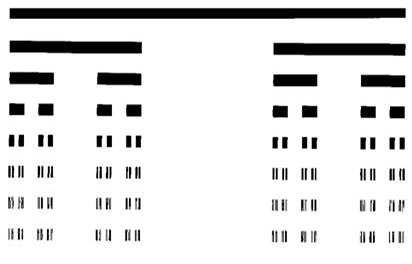



Рис. 1 Пыль Кантора

Понятие фрактал было предложено Бенуа Мандельбротом в 1975 году для обозначения самоподобных объектов, которыми он занимался. Появление фрактальной геометрии обычно связывают с выходом в 1977 году книги Мандельброта «The Fractal Geometry of Nature» (Фрактальная геометрия природы). Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"[1]. В своих работах он также использовал научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф).

Математическая база для появления теории фракталов была заложена за много лет до рождения Бенуа Мандельброта, но развиться она смогла лишь с появлением вычислительных устройств. В самом начале своей научной деятельности Бенуа работал математическим аналитиком в исследовательском центре компании IBM, когда сотрудники центра трудились над передачей данных на расстояние. В ходе исследований ученые столкнулись с шумовыми помехами, из-за которых часть данных терялась. Бенуа Мандельброт изучал эти шумы в электронных схемах, которые невозможно было описать с помощью статистики, и, просматривая результаты измерений шума, он заметил закономерность — графики шумов в разном масштабе выглядели одинаково. Идентичная картина наблюдалась независимо от того, был ли это график шумов за один день, неделю или час. Стоило изменить масштаб графика, и картина каждый раз повторялась. Вскоре это стало одним из основных свойств фракталов, когда небольшая часть фрактала содержит информацию о всем фрактале.

Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется задать линии и поверхности очень сложной формы. С точки зрения графики, фрактальная геометрия незаменима при генерации природных объектов, таких как искусственные облака, горы, поверхности морей и т.д.

2. Классификация фракталов.

Для того, чтобы понять всё многообразие фракталов, удобно прибегнуть к их общепринятой классификации. Фракталы как правило разделяют на две крупные категории: созданные учёными и фрактальные объекты природы. В свою очередь, созданные учёными разделяются еще на три группы:

• 
  Геометрические фракталы
  
• 
  Алгебраические фракталы
  
• 
  Стохастические фракталы
  

1. Геометрические фракталы

История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса — самые наглядные, потому что в них сразу видна самоподобность. В двухмерном случае геометрические фракталы получают с помощью некоторой ломаной, называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.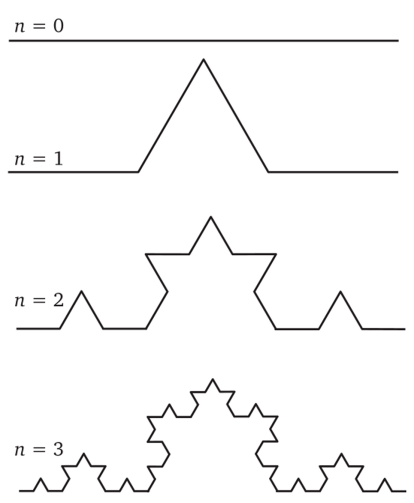



Рис. 2 Триадная кривая Коха

Рассмотрим один из таких фрактальных объектов - триадную кривую Коха. Построение кривой начинается с отрезка единичной длины (рис.2) - это 0-е поколение кривой Коха. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.2 через n=1. В результате такой замены получается следующее поколение кривой Коха. В 1-ом поколении – это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис.2 представлены три поколения кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным обьектом.[1]

В графике геометрические фракталы могут использовать для получения изображений деревьев, кустов, береговой линии и т.д. Но помимо графики, фрактальная геометрия применяется и в повседневной жизни. Так в 1995 году фрактальную геометрию использовали при проектировании антенных устройств. Американский инженер Натан Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, после чего присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск. В данный момент американская фирма “Fractal Antenna System” разработала антенну нового типа. С помощью этих технологий можно отказаться от использования в мобильных телефонах торчащих наружных антенн. Так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.

2. Алгебраические фракталы

Вторая большая группа фракталов - алгебраические. Алгебраические фракталы - фракталы, которые строят на основе алгебраических формул.

Первые исследования в этом направлении относят к началу XX века и связывают с именами французских математиков Гастона Жюлиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жюлиа, в котором описаны множества Жюлиа - целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, поэтому оценить красоту открытых объектов было невозможно. Но всё изменилось с появлением компьютеров: люди первые иллюстрации алгебраических фракталов. Теперь же, когда персональные компьютеры стали достаточно мощными, появилось даже целое направление в искусстве - фрактальная живопись, причем заниматься ею может практически любой владелец компьютера.

Одним из популярных примеров алгебраических фракталов является множество Мандельброта (рис.3).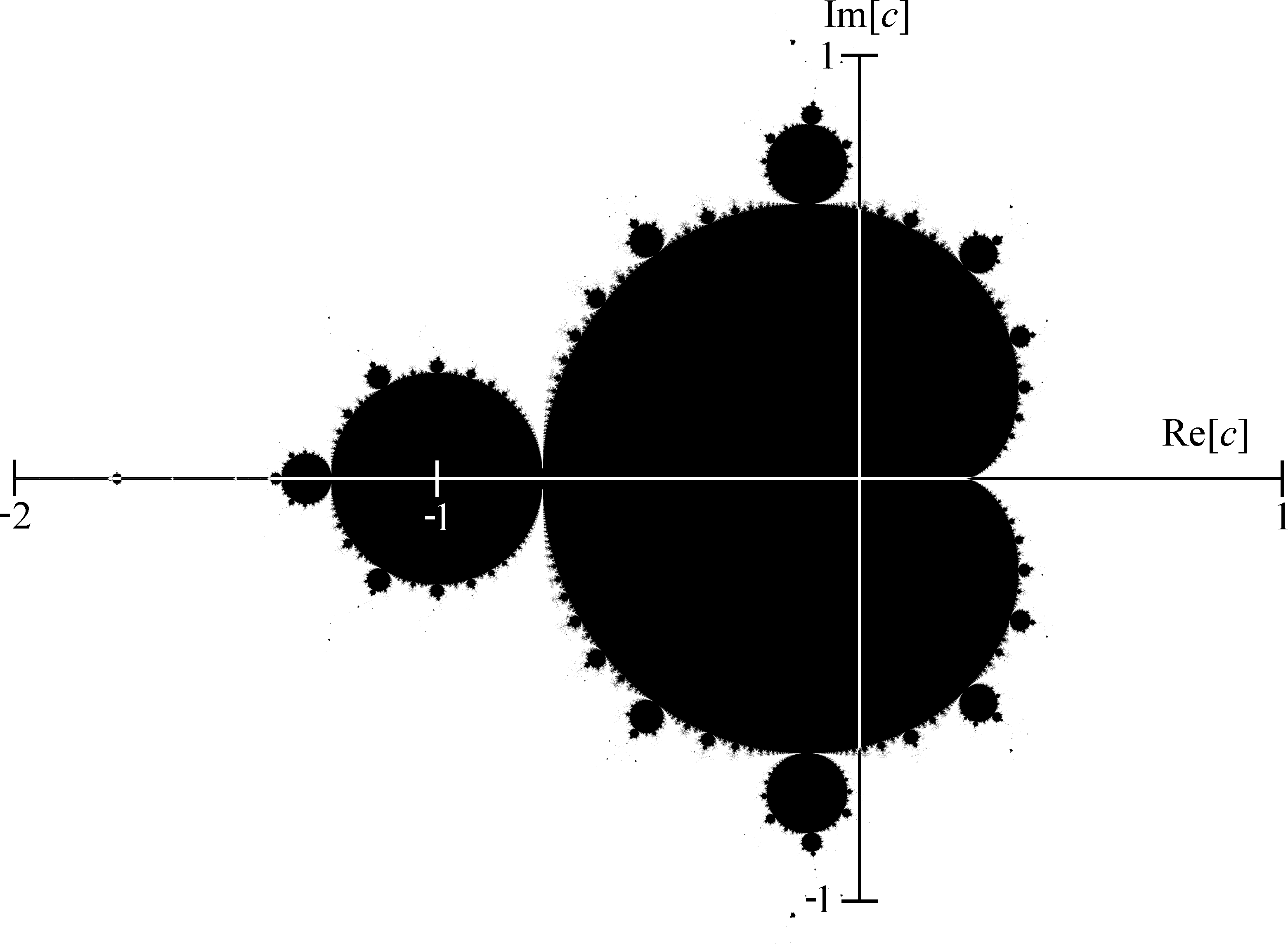



Рис. 3 Множество Мандельброта

3. 
   Стохастические фракталы
   

Третьей крупной разновидностью фракталов являются стохастические фракталы, которые образуются путем многократных повторений случайных изменений каких-либо параметров. Термин «стохастичность» происходит от греческого слова, обозначающего «предположение».

Наиболее ярким примером стохастического фрактала является траектория броуновского движения на плоскости и в пространстве.

Изменяя и комбинируя окраску стохастических фракталов, можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также составлять из полученных фигур «фрактальную композицию». Стохастические фракталы чаще всего можно увидеть в границах географических объектов и береговых линий, форме облаков и разрядах молний [2].



Рис. 4 Пример стохастического фрактала

4. 
   Физические фракталы
   

Фрактальные объекты, созданные природой, выделяют в один большой класс – физические фракталы. Основное и практически единственное их отличие от математических - отсутствие бесконечного самоподобия.

Частыми примерами являются: космическая пыль (рис.5), шаровая молния, облака и т.д.



Рис. 5 Фрактальная модель космической пылинки

На основе изученного материала мы составили классификацию фракталов в виде схемы (рис. 6).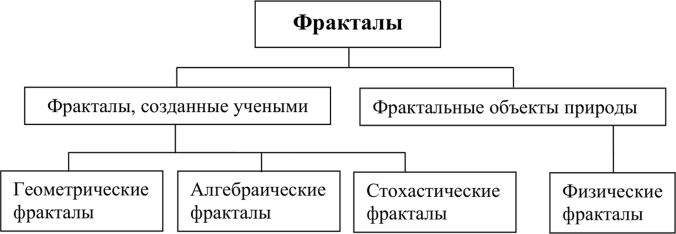



Рис. 6 Классификация фракталов

Глава 2. Создание фрактального изображения.

1. 
   Описание создания фрактального изображения.
   

Для получения изображения искусственно созданного фрактала мы выбрали редактор фрактальной графики Apophysis (рис.7).



Рис. 7 Главная страница приложения Apophysis

В самом редакторе мы использовали эффекты фракталов Spherical и Linear. С их помощью были сгенерированы узоры фрактала. Для того чтобы снежинка была симметричной, все треугольники были расположены точно по кругу, поэтому мы работали в полярной системе координат. Сначала нужно определить, сколько лучей будет у снежинки. В нашем случае их 8. Было рассчитано, под каким углом будут располагаться лучи снежинки по кругу.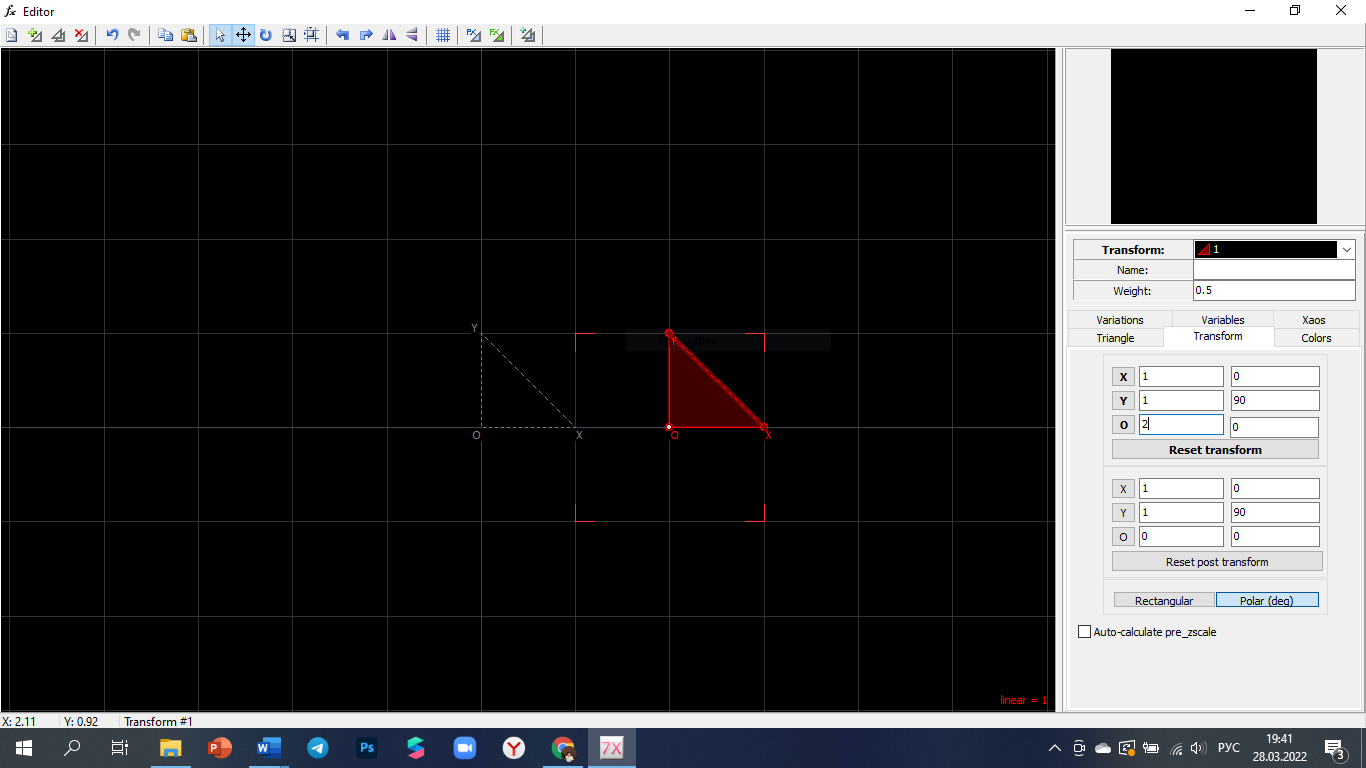



Рис. 8 Создание треугольника в редакторе

В редакторе программы был создан треугольник (рис.8) и выбраны характеристики, которые нам необходимы. Количество треугольников было увеличено до 8 для того, чтобы сгенерировать полное количество лучей снежинки.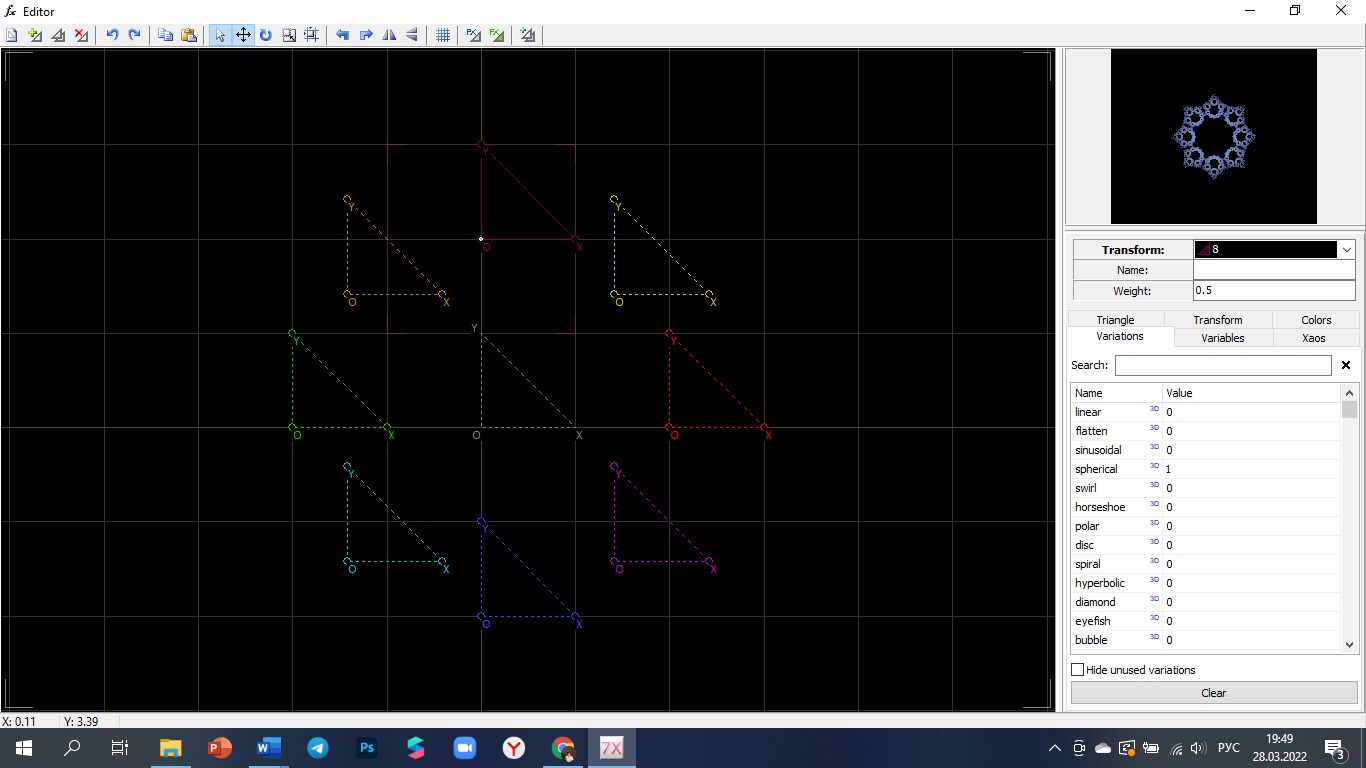



Рис. 9 Преобразование треугольников

Далее треугольники были преобразованы (рис. 9). Для каждого треугольника выставлялся конкретный угол, под которым он должен находиться, чтобы снежинка была симметрична. Таким образом была создана внешняя часть снежинки.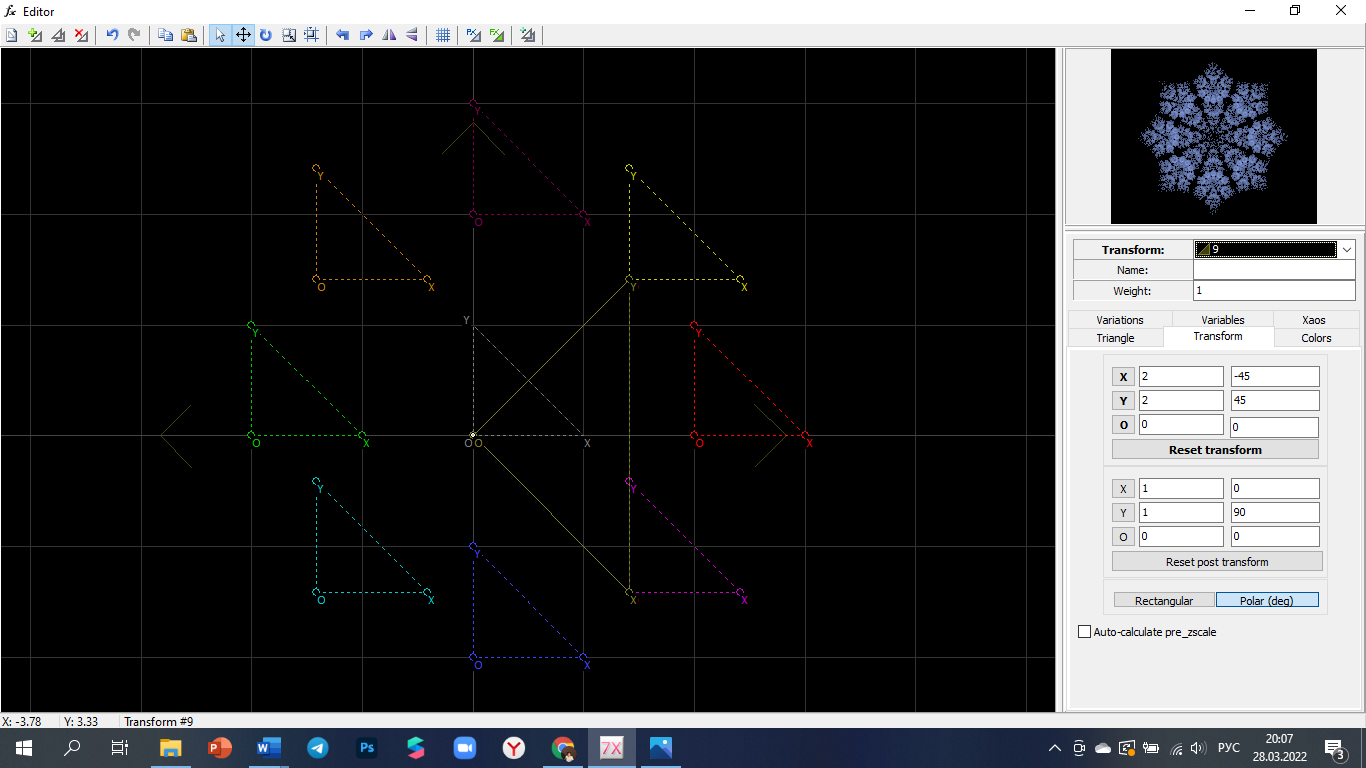



Рис. 10 Базовая форма фрактала

У нас уже получилось создать снежинку, но середина в ней пустая. Для того чтобы заполнить эту пустоту, необходимо создать еще один треугольник, но уже с другими параметрами. В результате, мы создали базовую форму фрактала (рис. 10).



Рис. 11 Фрактальное изображение снежинки

Чтобы наша снежинка была более реалистичной, мы задаём соответствующие ей цвета. В нашем случае был использован бело-голубой градиент. После рендеринга было получено изображение фрактала, похожего на снежинку (рис. 11).

1. 
   Сравнение фрактального изображения с реальным.
   

Для того чтобы объективно сравнить полученное фрактальное изображение с реалистичной снежинкой мы воспользовались крупнейшей поисковой системой интернета, принадлежащей корпорации Google Inc: Google. В качестве запросов в Google Поиске можно использовать изображения.

При использовании поиска по картинкам можно получить следующие результаты:

• 
  похожие картинки;
  
• 
  сайты, на которых размещено это изображение;
  
• 
  это же изображение других размеров.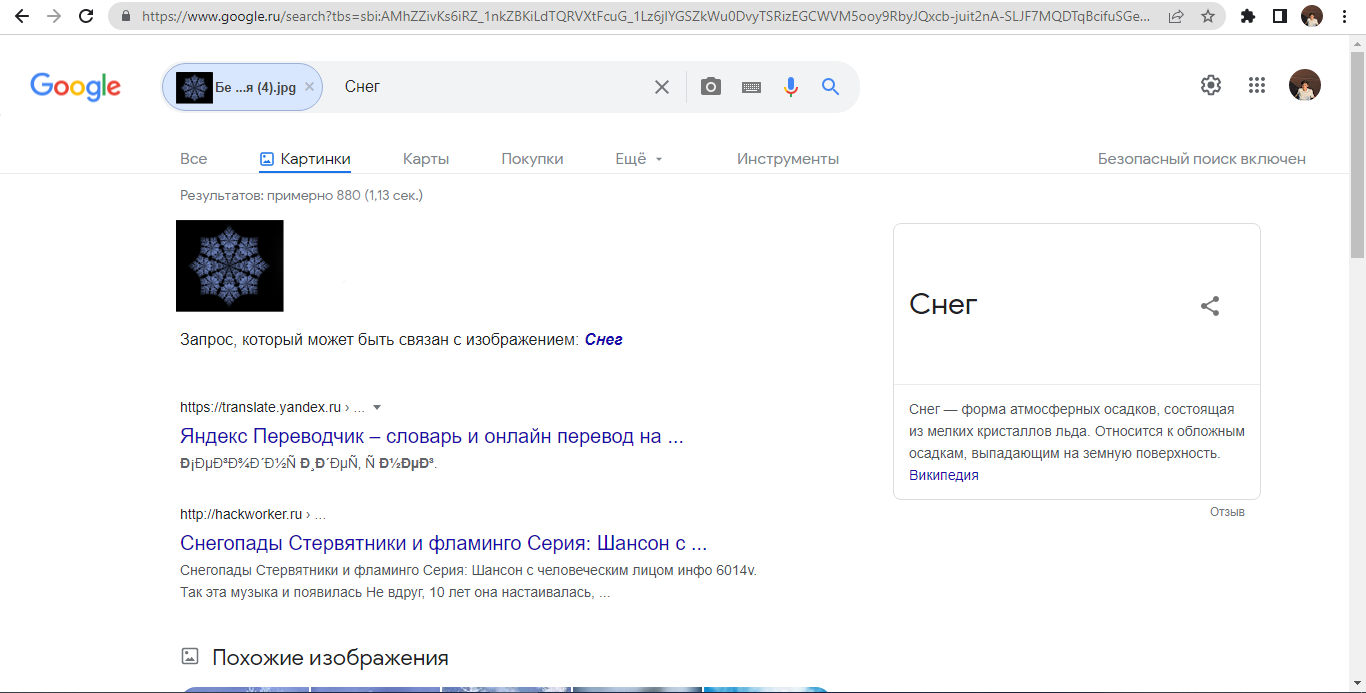
  

Рис. 12 Поиск по изображению в поисковой системе Google

Но главным является тот факт, что данная система позволяет определить, что находится на картинке, которую пользователь загрузил в поиск. Изображение фрактала, полученное нами, было загружено в данную систему. Результатом поиска было определение изображения – «снег» (рис.12).

Для верности эксперимента было проведено аналогичное исследование с использованием другой поисковой системы: «Яндекс» — поисковый движок, принадлежащий российской корпорации «Яндекс», основной продукт компании. Поиск по картинке основан на алгоритмах компьютерного зрения. В результате поиска могут быть найдены как точные копии исходного изображения, так и картинки, незначительно отличающиеся от оригинала.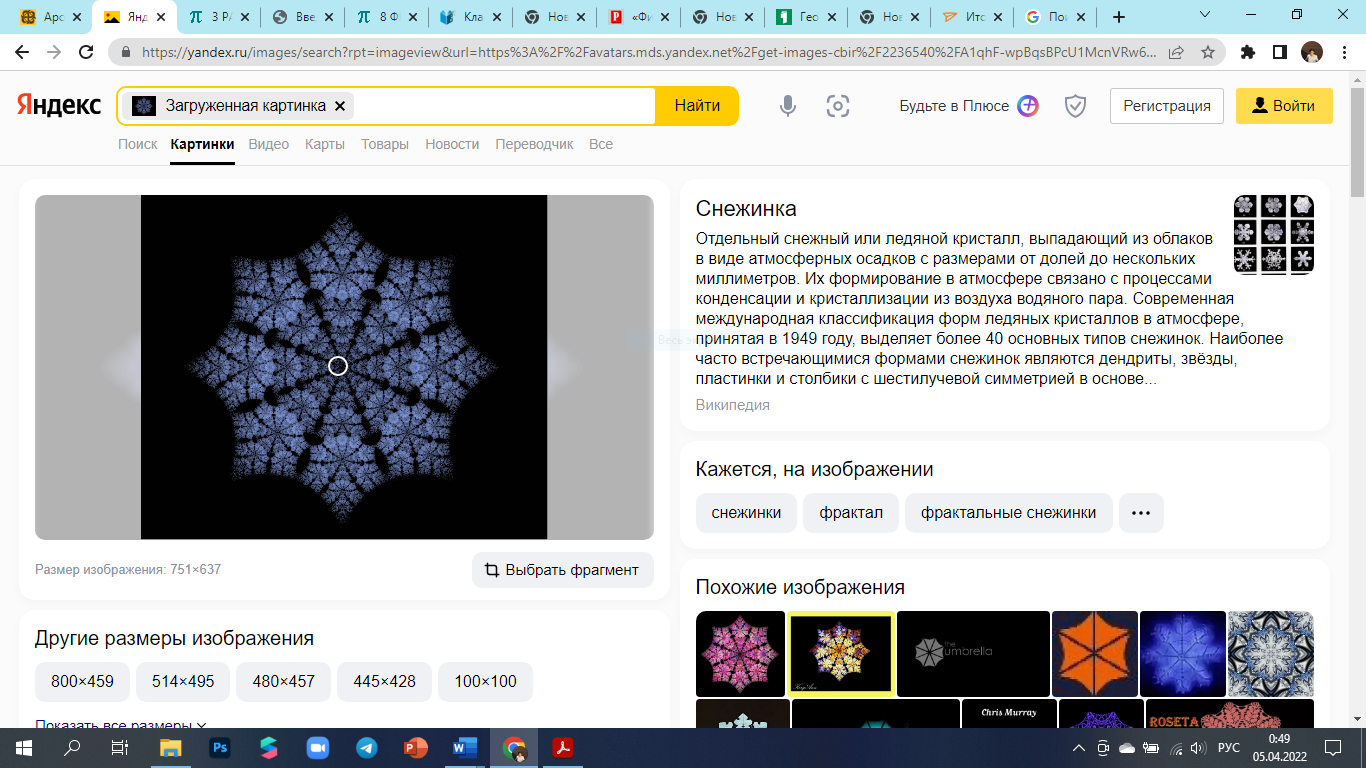



Рис. 13 Поиск по изображению в поисковой системе Яндекс

В данном случае система определила, что на изображении «снежинка» (рис. 13).

Проведенные действия показывают нам, что изображение искусственного фрактала снежинки имеет достаточную схожесть с реалистичными изображениями.

Заключение

На сегодняшний день фракталы незаметно входят в нашу жизнь. Они уже применяются в компьютерной графике. Пейзажи и текстуры, похожие на естественные появляются в кино и компьютерных играх, это является причиной более детального изучения фрактальной графики и её развития.

Проведенное исследование позволяет сделать следующие выводы:

1. 
   Под фракталом понимается структура, состоящая из частей, которые в каком-то смысле подобны целому. Выделяют два основных вида фракталов: созданные учёными и фрактальные объекты природы. Нами составлена обобщенная схема классификации.
   
2. 
   Использование фрактальной геометрии может открыть новые возможности в различных областях знаний, в том числе в информационных и коммуникационных технологиях.
   
3. 
   Простейшие фракталы можно построить, используя всего лишь чертежную линейку; для построения сложных фракталов с присутствием хаотических (случайных) воздействий возможно с использованием современных компьютеров и специализированных программ
   
4. 
   Фрактал способен повторять форму, черты и облик природных объектов.
   

В мире есть еще много интересного и неизученного в области фрактальной геометрии и графики.

“Трудно найти человека, равнодушного к фракталам. Многие считают, что знакомство с фрактальной геометрией подарило им совершенно неповторимые эстетические впечатления и обогатило новым научным опытом. В этом смысле фракталы безусловно оригинальны настолько, насколько это вообще возможно”. (Б. Мандельброт).

Список литературы

1. 
   Федер Е. Фракталы. Пер. с англ.-М. 1991. 254с.
   
2. 
   Ватолин, Д. Применение фракталов в машинной графике // Computerworld, Россия.1995. 11c.
   
3. 
   Мандельброт Б.Б. Фрактальная геометрия природы. Пер. с англ. Логунов.А.Р. 2002. 656с.
   
4. 
   Открытый урок, https://urok.1sept.ru/articles/518889
   
5. 
   Шабаршин А.А. Введение во фракталы. Екатеринбург.199
   

Приложение 1

Продукт проекта. Фрактальное изображение (рис.1).



Рис. 1 Фрактальное изображение