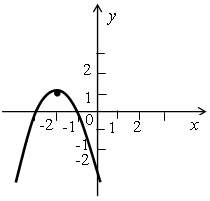Функция у х n

• Название: Функция у х n
• Дата: 16.11.2022
• Размер: 44.63 Kb.
• Имя файла: funktsiya_yxn.docx
• Тип: Урок; #792828

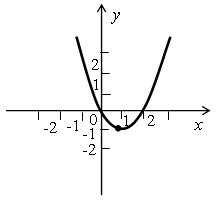
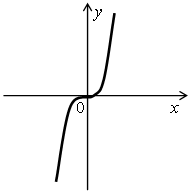
Урок алгебры в 9 классе. Автор учебника Макарычев Ю.Н.

Тема: «Функция у = хⁿ».

Цели: изучить свойства и график степенной функции; формировать умение строить и различать графики степенных функций с четными и нечетными показателями.

Ход урока

I. Организационный момент.

II. Проверка усвоения изученного материала.

1. 
   Проверка домашнего задания.
   
2. 
   Устная работа.
   

№1 Определите, график какой функции изображен на рисунке:

а) у = х2 + х – 1; б) у = х2 – 2х; в) у = –х2 + 2х; г) у = х2 – 2х – 1.

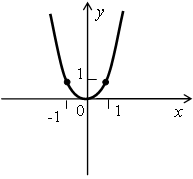
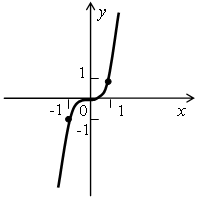
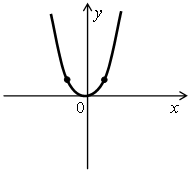
№2 Определите, график какой функции изображен на рисунке:

а) у = –х2 – 2х + 1; б) у = х2 + 4х – 3; в) у = –х2 – 4х – 3; г) у = –х2 + 2х.

3. 
   Постройте график функции
   

а) у = х² + 4х + 2; б) у = –2х² + 4х + 1.

III. Объяснение нового материала.

При изучении степенной функции следует больше внимания уделить самостоятельной работе учащихся, предложив им сделать основные выводы и перечислить свойства новой функции.

О б ъ я с н е н и е может быть построено по следующей схеме:

1. Предложить учащимся построить в одной системе координат графики функций у = х², у = х⁴ и у = х⁶, заполнив таблицы значений этих функций.

х	–2	–1,5	–1	–0,5	0	0,5	1	1,5	2
у

Затем задать учащимся в о п р о с ы:

– В чем состоит сходство построенных графиков?

– Чем отличаются графики функций?

– Как будут выглядеть графики функций у = х⁸ и у = х¹⁰?

– Может ли функция у = х¹⁸ принимать отрицательные значения?

2. Предложить учащимся в одной системе координат построить графики функций у = х³ и у = х⁵, а затем ответить на следующие в о п р о с ы:

– В чем состоит сходство построенных графиков?

– Чем отличаются графики функций?

– Как будет выглядеть график функции у = х⁷?

– Может ли функция у = х⁹ принимать отрицательные значения?

3. Сообщить учащимся, что функции, графики которых они строили, называются степенными функциями с натуральным показателем и записываются в общем виде:

у = хп

Далее спросить учащихся, на какие две группы можно разбить все степенные функции, и предложить им перечислить свойства каждой из выделенных групп.

у = х2п	у = х2п + 1
1) D (у) = R; 2) Е (у): [0; +∞); 3) у = 0 при х = 0; 4) если х ≠ 0, то у > 0; 5) : [0; +∞), : (–∞; 0].	1) D (у) = R; 2) Е (у) = R; 3) у = 0 при х = 0; 4) у > 0, если х (0; +∞), у < 0, если х (–∞; 0); 5) Функция возрастающая.

IV. Формирование умений и навыков.

На этом уроке основное внимание следует уделить заданиям на изображение и различение графиков степенных функций, а также на использование их свойств.

Упражнения:

1-я г р у п п а.

1. Определите, график какой функции изображен на рисунке:

а)	у = х16 у = –2х10 у = х11 у = х2 + 2х
б)	у = х2 – 4х у = х3 у = х9 у = х12

2. № 142.

3. № 145 (в, г), № 146.

2-я г р у п п а.

1. № 136, № 137.

2. Функция задана формулой f (х) = х³². Сравните:

а) f (1,7) и f (4); в) f (–5) и f ;

б) f (–2,1) и f ; г) f (20) и f (–17).

3. Функция задана формулой g (х) = х³⁷. Сравните:

а) f (3,6) и f (4,7); в) f (50) и f (–40);

б) f и f (–2); г) f (25) и f (–25).

V. Итог урока. Рефлексия.

В о п р о с ы у ч а щ и м с я:

– Какая функция называется степенной функцией с натуральным показателем?

– На какие две группы можно разделить степенные функции?

– Перечислите свойства степенной функции с четным показателем.

– Перечислите свойства степенной функции с нечетным показателем.

Домашнее задание: п. 8 № 138, № 139, № 143, № 145 (а, б).