Контрольная по математике. Где числа, i m,, j n, называются коэффициентами системы, числа свободными членами
 Скачать 28.24 Kb. Скачать 28.24 Kb.
|
|
1. Решить систему линейных алгебраических уравнений: 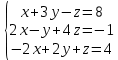 Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида 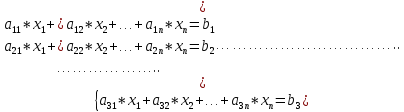 (1) (1)где числа 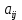 , i 1,...m, , j=1,...n, называются коэффициентами системы, числа , i 1,...m, , j=1,...n, называются коэффициентами системы, числа 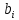 - свободными членами. - свободными членами.Решением системы линейных уравнений (1) называется такая совокупность n чисел ( 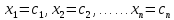 ), при подстановке которых в каждое из уравнений системы обращается в тождество. ), при подстановке которых в каждое из уравнений системы обращается в тождество.Систему (1) можно записать в матричной форме: A*X=B , где A= 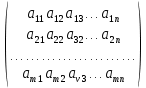 - матрица системы, X= - матрица системы, X= – столбец неизвестных, – столбец неизвестных,B= 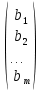 - столбец свободных членов. - столбец свободных членов.В нашем задании число уравнений равно числу переменных: n=m. Тогда матрица А системы является квадратной, а ее определитель 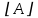 называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной. Решение невырожденной системы выполняем методом Крамера. называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной. Решение невырожденной системы выполняем методом Крамера.Если определитель матрицы системы (1) n линейных уравнений с n неизвестными отличен от нуля, то данная система имеет единственное решение, которое находится по формулам: 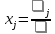 , j=1,2…n, (3) , j=1,2…n, (3)где - определитель матрицы A , а определитель j - определитель матрицы который получается после замены в матрице А j - го столбца на столбец свободных членов. Формулы (3) называют формулами Крамера. Если определитель системы A 0, то система линейных алгебраических уравнений совместна, и ее решение может быть найдено по формулам Крамера: x 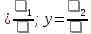 ; ; 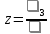 . Составим матрицу А коэффициентов системы: A= . Составим матрицу А коэффициентов системы: A=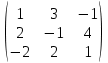 , найдем определитель системы = , найдем определитель системы =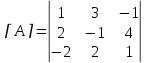 . Определитель высчитывается по формуле: . Определитель высчитывается по формуле: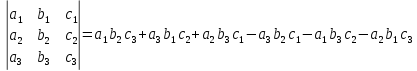 . (4) . (4)= 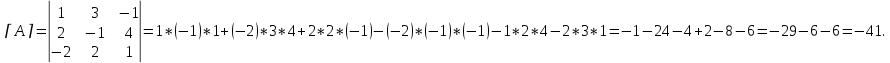 Затем вычислим определители 1, 2, 3 . 1 получается из определителя заменой первого столбца на столбец свободных членов (правые части уравнения): 1= 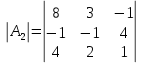 =8*(-1)*1=4*3*4+(-1)*2*(-1)-4*(-1)*(-1)-8*2*4-(-1)*3*1=-8+48+2-4-64-(-3)=-23. =8*(-1)*1=4*3*4+(-1)*2*(-1)-4*(-1)*(-1)-8*2*4-(-1)*3*1=-8+48+2-4-64-(-3)=-23.2 получается из определителя заменой второго столбца на столбец свободных членов: 2 = 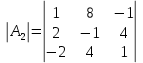 =1*(-1)*1+(-2)*8*4+2*4*(-1)-(-2)*(-1)*(-1)-1*4*4-2*8*1= =1*(-1)*1+(-2)*8*4+2*4*(-1)-(-2)*(-1)*(-1)-1*4*4-2*8*1==-1-64-8+2-16-16=-73+2-32=-103. 3 получается из определителя заменой третьего столбца на столбец свободных членов: 3= 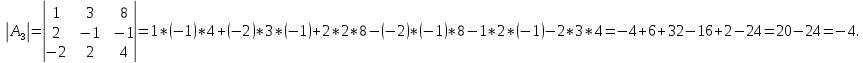 В итоге получим решение системы: x  = =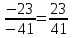 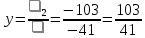 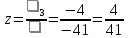 . .Ответ: ( 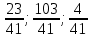 ). Проверка осуществляется подстановкой чисел x= ). Проверка осуществляется подстановкой чисел x=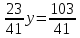 z= z=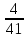 в каждое уравнение исходной системы. в каждое уравнение исходной системы.2. Дано z1=1-5i z2=3+2i Выполнить действия: a) z1+z2 б) z1*z2 в) z1/z2 a) Для комплексных чисел z1 = x1 + iy1, z2 = x2 + iy2 сумма и разность находятся по формулам z1 ± z2 = (x1 ± x2) + i(y1 ± y2). В нашем случае имеем z1 + z2=(1+3)+i(-5+2)=4-3i б) Перемножаем z1 и z2 как двучлены с учетом равенства i2 = -1: z1*z2 =(1-5i)*(3+2i)=1*3-15i+2i-10*(-1)=3-15i+2i+10=13+i(-15+2)=13-13i в) Для нахождения частного 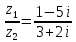 умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю, т.е. на 3 – 2i; получим умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю, т.е. на 3 – 2i; получим 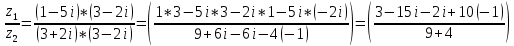 = =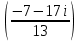 = =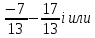 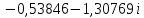 . .3. Найти математическое ожидание и дисперсию функции, заданной законом распределения:
Свойства дискретных случайных величин: все их значения можно перенумеровать натуральными числами; каждому значению сопоставить отличную от нуля вероятность. Поочередно умножаем пары: xi на pi. Складываем произведение каждой пары xi*pi. В задании для n = 4: m = ∑xipi = x1p1 + x2p2 + x3p3 + x4p4. Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. M[X]=2*0.4+3*0.3+4*0.1+5*0.2=0.8+0.9+0.4+1=3,1. Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]=22*0,4+32*0,3+42*0,1+52*0,2-3,12=4*0,4+9*0,3+16*0,1+25*0,2-3,12=1,6+2,7+1,6+5-9,61=1,29. 4. Вычислить предел 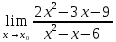 при x0=2 при x0=2Подставляем число x0=2 в функцию 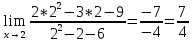 5. Найти производную функции y= 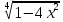 6. Вычислить неопределенный интеграл 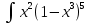 dx dx |
