курсовой проект. 1 Гео КУрсач Microsoft Office Wordvfr. Геодезический курс при землеустройстве

• Название: Геодезический курс при землеустройстве
• Анкор: курсовой проект
• Дата: 28.09.2022
• Размер: 0.67 Mb.
• Имя файла: 1 Гео КУрсач Microsoft Office Wordvfr.docx
• Тип: Документы; #702607
• страница: 2 из 7

y_{9 –10} =y₁₀ –y₉ ∆y_{9 –1} =y₁ –y₉
По найденным значениям приращений координат ∆xи ∆y, вычислим табличный угол

^tgr9 –10 ^{= ∆y}9 –10 ^/∆x9 –10 ^tgr9 –1 ^{= ∆y}9 –1 ^/∆x9 –1

отсюда

r= arctg|∆y/∆x|

По знакам приращений координат ∆xи ∆y определено, в какой четверти находится данное направление. Затем, руководствуясь со- отношением между табличным и дирекционным углами, находим дирекционный угол направлений 9-10и 9-1 .

Подставим значения в формулы (3) и (2).

Таблица 2 - Результаты вычисления площади участка сенокоса с прудом

№ точек	Координаты, м		Разности координат, м		r = arctg|∆y/∆y|	α	β9=α9-10 - α9-1
	Х	У	Xi - Xi-1	Yi - Yi-1
1	1200	1500	5,6	735,6	89,56	89,56	80,74
9	1194,4	764,4
			-905,6	154,8	9,70	170,30
10	288,8	919,2
P=2,50			2P(м3) = absinβ9 + bcsinφ + acsin (β9+φ-180) =					49933,15683
			P =					24966,57842

^9 ^{ }910 ^91 ^{, (3)}

Подставляем значения в формулу и подсчитываем P

P = 49933,16 (м²)

P= P/20000 = 49933,16/20000 = 2,50 (га)

Вычисляем площадь пруда по данным абриса, используя формулу

трапеции:

Р_трап. = 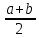h (4)

а = 86,66 (м)

b = 40,6 – 33,8 = 6,8 (м)

h = 124,1 – 48,7 = 75,4(м)

Р_пруда= (86,66 + 6,8) 75,4/2 = 3523,49/10000 = 0,35 (га)

Площадь пруда в северной части:

а =85,91 (м)

b= 112,56 (м)

h= 69,39 (м)

Р_пруда= (85,91 + 112,56)69,39/2 = 6352,7/10000 = 0,64 (га)
Площадь проектируемой дороги в фермерском хозяйстве вычис-

ляем по формуле:

^Рдор,(га)

 b 5( м²) (5)

Р_дор. = 183,3  5/10000 = 0,09 (га)

Результаты вычислений округляем до 0,01 га и заносим в табл.3.

Таблица 3 – Состав площадей

Название угодий	Площадь, га
Сенокос	2,15
Под водой	0,35
Всего	2,50
Дорога	0,09

В соответствии с рисунком 3, по результатам измерений в натуре вычисляем площадь леса. Для этого рассчитываем угол при точке 3 как разность дирекционных углов линий 3-2 и 3-4.

Площадь леса вычисляем по формуле:

^2P_{лесга}^a₁ ^c₁ ^d₁ ^{sin }₃ ^b₁ ^c₁ ^d₁ ^{sin a}₁^b₁ ^sin _^{}₃ ^{180) (6)}

Результаты вычислений округляем до 0,01 га и заносим в табл.4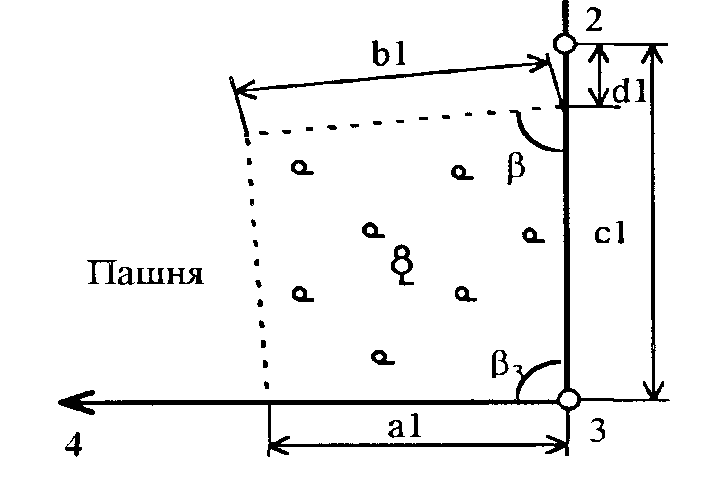

Рисунок 3. Схема участка леса
а₁= 173,4 м; b₁ = 304,8 м; d₁ =100,9 м; с₁ = S_2-3;  = 4732
S_2-3 = =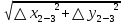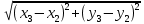

Таблица 4 - Результаты вычисления площади участка леса

№ точек	Координаты, м		Разности координат, м		r = arctg|∆y/∆y|	α	β3=α3-2 - α3-4
	Х	У	Xi - Xi-1	Yi - Yi-1
2	13,4	1501,4	879,6	-5,9	0,38	359,62	101,87
3	-866,2	1507,3
			-333,3	-1535	77,75	257,75
4	-1199,5	-27,7
P=14,02			2P(м3) = acsinβ3 + bcsinβ + absin (β3+β-180) =				280328,9725
			P =				140164,4862

3 ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ УЧАСТКОВ ГРАФИЧЕСКИМ (ГРАФОАНАЛИТИЧЕСКИМ) СПОСОБОМ

Графический способ определения площадей по плану иначе называют геометрическим. Состоит в том, что участки, изображённые на плане, разбивают на простые фигуры: треугольники, трапеции, параллелограммы.

Графический способ менее точен, потому что, помимо погрешностей измерений на местности на точность вычисленной площади влияют погрешности составления плана и определения площади по плану, применяют для определения площадей и землепользований, и полей севооборотов, и контуров угодий, ограниченных ломаными линиями,

Площади различных геометрических фигур вычисляют по формулам:

для треугольника: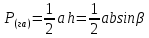

где a, b, c– горизонтальное проложение сторон в метрах;

h– высота в метрах;

β– угол между сторонами aи bтреугольника, для параллелограмма: ^P_(га) ^{ ah}

длятрапеции: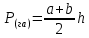

для четырехугольника: _{2P( га)}  absin _{ 1}  cdsin _{ 2}

где _1 , _2 – углы между соответствующими сторонами.
Определяем графическим способом площадь производственного центра, разбив его на простейшие геометрические фигуры – 3 треугольника и 2 трапеции. В каждой фигуре на плане измеряем высоту и основание, по которым вычисляем площадь, используя следующие формулы: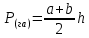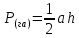

;

где h– высота в метрах;

a– основание в метрах;

b – основание в метрах.
Таблица 5 - Результаты вычисления площади участка производственного центра

Тип фигуры	Высота, м	Нижнее основание, м	Верхнее основание, м	Площадь, га
Треугольник 1	381,61	773,75	-	14,76
Треугольник 2	308,4	426,18	-	6,57
Треугольник 3	126,09	140,95	-	0,89
Трапеция 1	139,08	308,4	143,08	3,14
Трапеция 2	82,4	143,08	140,95	1,17

Сумма площадей фигур даст площадь производственного центра.