Практическое занятие, способы определения площадей в землеустройстве. СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ ПРИ ЗЕМЛЕУСТРОЙСТВЕ. Способы определения площадей при землеустройстве характеристика способов определения площадей землепользования и землевладений
 Скачать 81.64 Kb. Скачать 81.64 Kb.
|
|
СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ ПРИ ЗЕМЛЕУСТРОЙСТВЕ 1. Характеристика способов определения площадей землепользования и землевладений Составление различного рода проектов, связанных с использованием земельной территории, изучение ее природных богатств, учет и инвентаризация земель требуют определения площадей. При проведении этих работ определяют небольшие площади строений, сооружений, уличных проездов, площадей, парков, усадебных участков, огородов и большие площади – городов или сельских населенных пунктов, целых землепользований и севооборотных массивов. Наряду с величиной площади требуется знать и точность ее определения. В зависимости от хозяйственной значимости участков и массивов, их размеров, конфигурации и вытянутости, наличия результатов измерения линий и углов на местности и планово-картографического материала, а также топографических условий местности применяются следующие способы определения площадей. 1. Аналитический: площадь вычисляется по результатам измерений линий и углов на местности или по их функциям – координатам вершин фигур. 2. Графический: площадь вычисляют по результатам измерений линий и углов (транспортиром) или по координатам точек на плане (карте). 3. Механический: площади определяют на плане при помощи специальных приборов (планиметров, картометров) и приспособлений (палеток, ротометров). Нередко эти способы применяют комбинированно. Наиболее точным, но требующим больших материальных затрат на производство полевых измерений, является аналитический способ, так как его точность не зависит от точности плана. Его применяют для вычисления площадей, когда по их границам проложены теодолитные ходы и полигоны, а также при обмере ценных в хозяйственном отношении участков. Менее точен графический способ, так как, помимо погрешностей измерений на местности, на точность влияет погрешность плана. Его применяют для определения площадей, ограниченных ломаными линиями. Чем меньше площадь участка, тем больше относительная погрешность. Для больших площадей точность этого способа приближается к точности аналитического. Наименее точным, но наиболее распространенным является механический способ, так как, пользуясь им, можно быстро и просто определить площадь участка любой формы. Его применяют при определении площадей с извилистыми границами. 2. Аналитический способ Если граница какой-либо территории наложена на план по координатам, то можно по ним вычислить ее площадь, заключенную в многоугольник. Вычисление производится по формуле 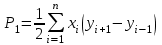 , т.е. площадь многоугольника равна полусумме произведений каждой абсциссы на разность ординат последующей и предыдущей вершин многоугольника. , т.е. площадь многоугольника равна полусумме произведений каждой абсциссы на разность ординат последующей и предыдущей вершин многоугольника.Контролем служит формула 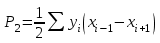 , т.е. площадь P многоугольника равна полусумме произведений каждой ординаты y на разность абсцисс x предыдущей и последующей вершин. Расхождение между P1 и P2 не должно превышать 0.1 м2. , т.е. площадь P многоугольника равна полусумме произведений каждой ординаты y на разность абсцисс x предыдущей и последующей вершин. Расхождение между P1 и P2 не должно превышать 0.1 м2.Для вычисления площади треугольника и четырехугольника пользуются формулами, состоящими из двух произведений. Для треугольника: 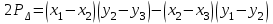 , или , или 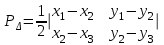 . .Для четырехугольника: 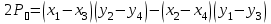 , или , или 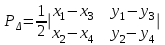 . .Значение координат для площадей менее 200 га округляют до 0.1 м, для больших площадей – до 1.0 м. Относительная погрешность определения площади аналитическим способом несколько больше относительной погрешности измерений линий, но относительные погрешности вычисления площадей полигонов, включенных в геодезическую сеть, значительно меньше 1/2000 (т.е. погрешности измерения линии). 3. Графический способ Вычисление площадей графическим способом состоит в том, что участки, изображенные на плане, разбивают на простейшие геометрические фигуры – преимущественно на треугольники, реже – на трапеции. В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь. Сумма площадей фигур дает площадь участка. Чем больше углов имеет граница участка, тем меньше эффективность этого способа. Следовательно, для определения площадей участков, имеющих большое количество углов, целесообразно вычислять площадь по графическим координатам точек, т.е. координатам, измеренным на плане при помощи измерителя или координатографа, координатометра и др. Наилучшим вариантом разбивки участка на треугольники будет тот, при котором треугольники близки к равносторонним (вернее, их высоты близки по величине к основаниям). Если высоты или основания, по которым определяют площади фигур, представляют линии, измеренные на местности, например, стороны теодолитного полигона, то для повышения точности определения площадей на плане длины этих линий не измеряют, а принимают величины, полученные на местности. Точность вычисления площади неравностороннего треугольника будет выше, если короткое основание (или высота) измерено на местности, а длинная высота (или основание) определена по плану. Для контроля и повышения точности площадь каждого треугольника определяют дважды: по двум различным основаниям и двум высотам. Если расхождение допустимо, то из двух значений площади вычисляют среднее. Допустимость расхождения между двумя значениями площади определяют по формуле 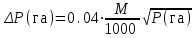 , ,где M – знаменатель численного масштаба плана. Для обеспечения контроля вычислений и повышения точности при выборе высот и оснований не следует стремиться к тому, чтобы в смежных треугольниках они повторялись, так как это ведет к зависимости результатов вычислений, и могут оказаться незамеченными грубые ошибки. Пример вычисления графическим способом площади полигона (рис. 12) приведен в табл. 1. 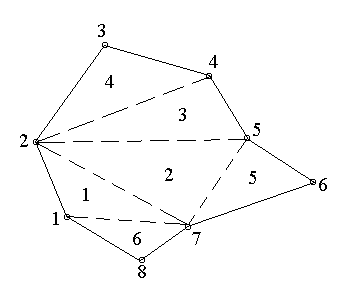 Рис. 12 Т а б л и ц а 1
4. Вычисление площадей с помощью палетки Для определения площадей небольших участков с криволинейными контурами на плане применяют палетки, в основном прямолинейные. К прямолинейным палеткам относятся известные и наиболее распространенные квадратные и параллельные палетки. Квадратная палетка представляет собой сеть взаимно перпендикулярных линий, проведенных через 1–2 мм на прозрачном целлулоиде, плексигласе, фотопленке, стекле или кальке. Площадь фигуры определяется простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитываются на глаз (рис. 13). Квадратной палеткой не рекомендуется определять площади больше 2 см2 на плане. Недостаток ее применения (помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз) в том, что подсчет количества целых клеток нередко сопровождается грубыми погрешностями. 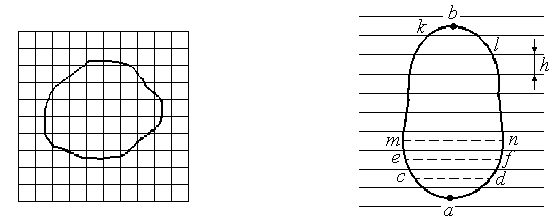
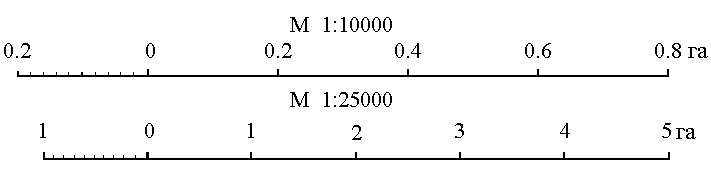 Рис. 15 Такие недостатки не наблюдаются при определении площадей параллельной палеткой, представляющей собой листок прозрачного целлулоида, плексигласа или кальки, на котором нанесены параллельные линии преимущественно через 2 мм одна от другой. Площадь контура определяют этой палеткой следующим образом. Накладывают ее на контур так, чтобы крайние точки a и b разместились посредине между параллельными линиями палетки. Тогда, весь контур оказывается разделенным параллельными линиями на фигуры, близкие к трапециям, с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций (рис.14). Пунктиром показаны основания этих трапеций. Сумма площадей трапеций, т.е. площадь контура, равна 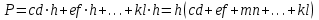 . .Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т.е. сумму отрезков параллельных прямых внутри контура, и умножить на расстояние между ними. Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля, которую определяют по масштабной линейке и полученную длину умножают на h, м (рис.15). Чтобы не выполнять подобных вычислений, для каждого масштаба строят специальную шкалу, по которой отсчитывают площадь контура, зная сумму средних линий. Расчет шкалы: М 1:10000, h = 2 мм, при длине шкалы 1 см площадь равна (0.2 см 100 м) (1 см 100 м) = 2000 м2 = 0.2 га. Параллельной палеткой не следует определять площади больше 10 см2 на плане. 5. Точность вычисления площадей графическим способом и с помощью палетки При разбивке участка на простейшие фигуры точность вычисления для различных вариантов не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее, чем площади других фигур. Следовательно, площадь при разбивке участка на треугольники вычисляется точнее, чем при разбивке на другие фигуры (трапеции, прямоугольники). При разбивке участка на треугольники из всех вариантов будет лучшим тот, в котором треугольники будут равносторонними или высота h примерно равна основанию a. Погрешность уменьшается, если вычислять площадь треугольника не как 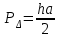 , а по формуле Герона , а по формуле Герона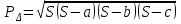 , ,где 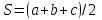 . Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если оно измеряется на местности, а не на плане. . Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если оно измеряется на местности, а не на плане.При разбивке площади на треугольники погрешность площади участка 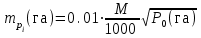 , ,где M – знаменатель численного масштаба плана. Если 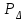 вычисляют два раза, то вычисляют два раза, то 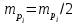 . .Число треугольников, на которое разбивается участок, не влияет на погрешность площади. Поэтому при разбивке участка на треугольники не надо стремиться к тому, чтобы их было меньше. Точность однократного определения площади квадратной и параллельной палетками, а также ротометром характеризуется эмпирической формулой 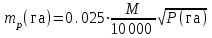 . .6. Механический способ определения площадей Механический способ определения площади фигуры любой формы состоит в обводе ее на плане при помощи механического прибора (планиметра). Планиметром называют механический прибор, дающий возможность путем обвода плоской фигуры любой формы определить ее площадь. Планиметры делятся на линейные (простейшие; например, топорик) и полярные наиболее распространенные. Полярный планиметр состоит из двух рычагов (обводного R и полюсного R0), соединенных шаровым шарниром. Обвод фигуры производится обводным индексом, расположенным на конце обводного рычага. Обводной индекс представляет собой либо конец шпиля, либо точку на нижней поверхности стекла. Площадь по результатам обвода определяют с использованием формул: 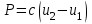 – при положении полюса вне фигуры, – при положении полюса вне фигуры, 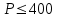 см2, см2,или 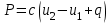 – при положении полюса внутри фигуры, – при положении полюса внутри фигуры, где u1 – начальный отсчет; u2 – конечный отсчет; c – цена деления планиметра; q – постоянная планиметра при установке его внутри контура искомой площади. Перед обводкой определяют q и c: 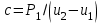 ; ; 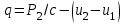 , ,где P1, P2 – известная площадь (обычно P1 – площадь километрового квадрата картографической сетки; P2 – площадь 4…6 таких квадратов). При работе с полярным планиметром следует соблюдать следующие правила. 1. При обводе контура угол между рычагами не должен быть меньше 30° и больше 150°. 2. Обводное колесо должно вращаться свободно. 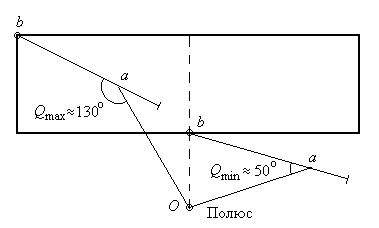 Рис. 16 Точку для начала обвода выбирают в том месте фигуры, где угол между рычагами наиболее близок к 90°, так как в этом случае погрешность отсчета минимальна (рис. 16). 7. Определение площади по способу Савича Способ Савича применяют для определения больших площадей, когда межевые знаки по границам не имеют вычисленных значений координат или границы проходят по кривым линиям живых урочищ. Сущность способа в том, что площадь участка, заключенная в целое число квадратов координатной сетки P0, определяется по их числу. Планиметром обводятся лишь площади секций, выходящие за пределы этих квадратов (рис.17) a1, a2,a3 и a4, и дополнения их до целого b1, b2,b3 и b4. Площади ai и bi обводят планиметром при двух положениях полюса по два обвода в каждом положении и выражают в делениях планиметра. Очевидно, что  . Искомая площадь участка . Искомая площадь участка  . Для исключения грубых промахов обводят всю фигуру планиметром при положении полюса внутри фигуры. . Для исключения грубых промахов обводят всю фигуру планиметром при положении полюса внутри фигуры.Преимущества способа Савича. 1. Автоматически учитывается деформация бумаги, на которой составлен план. 2. Уменьшается площадь обводимых фигур, что повышает точность определения площади.  Рис. 17 Точность определения площади по способу Савича тем выше, по сравнению с непосредственным обводом всей фигуры или по частям, чем больше отношение площади целых квадратов координатной сетки к площади всей фигуры. 8. Точность определения площади планиметром Средняя квадратическая погрешность mp определения площади P зависит от средней квадратической погрешности цены деления планиметра c и средней квадратической погрешности числа делений  . Она не может быть меньше 0.7 деления планиметра, а относительная средняя погрешность не может быть меньше 1:1000. . Она не может быть меньше 0.7 деления планиметра, а относительная средняя погрешность не может быть меньше 1:1000.Общая средняя квадратическая погрешность: 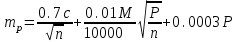 при при 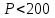 см2 на плане; см2 на плане;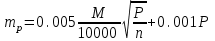 при при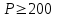 см2 на плане, см2 на плане,где c – цена деления планиметра; n – количество обводов; M –знаменатель численного масштаба; P – площадь, га. Погрешность площадей, определенных планиметром, очень велика для очень узких вытянутых полос. Основное геометрическое условие планиметра – направление рифельных штрихов на ободке счетного ролика должно быть параллельно оси обводного рычага. | ||||||||||||||||||||||||||||||||||
