Лобачевский. Геометрия лобачевского
 Скачать 495.87 Kb. Скачать 495.87 Kb.
|
|
Лобачевский Николай Иванович – народный просветитель, математик. ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО История геометрии Лобачевского — это история попыток доказать пятый постулат Евклида. Этот постулат - одна из основных геометрических аксиом Евклида. Пятый Постулат Евклида если две прямые пересекаются третьей таким образом, что с любой стороны от нее сумма внутренних углов меньше двух прямых углов, то прямые линии пересекаются на этой стороне. 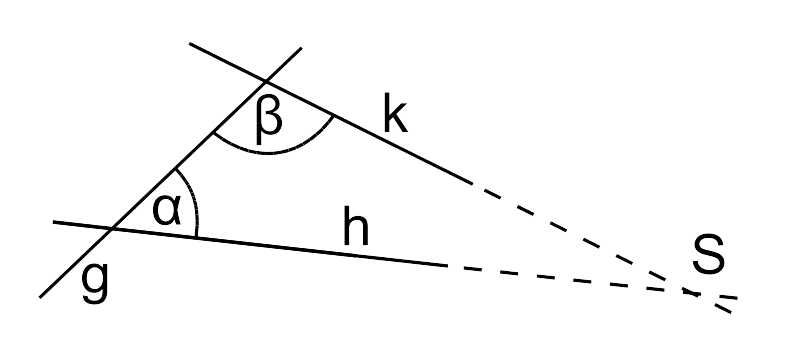 Многие математики, жившие после Евклида, пытались доказать, что эта аксиома может быть доказана как теорема на основе других аксиом, но все потерпели неудачу. И только в XIX веке эту загадку решил профессор Казанского университета Лобачевский. Он пытался вывести различные последствия, основываясь на отрицании пятого постулата, надеясь, что рано или поздно он придет к противоречию. Однако он доказал многие десятки теорем, не обнаружив логических противоречий. А потом он догадался, что геометрия, в которой пятый постулат заменен его отрицанием, не противоречит. Лобачевский назвал эту геометрию воображаемой. Она кардинально изменила наше понимание физической реальности и повлияла на исследования Альберта Эйнштейна и открытие им теории относительности. Геометрия Лобачевского – одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных аксиомах, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием. «Через точку Р вне данной прямой проходит более одной прямой, параллельной данной» Этим утверждением два математика Лобачевский и Бойяи почти одновременно решили проблему постулата о параллельных прямых, и поэтому они являются основоположниками первой неевклидовой геометрии. Они оба считаются авторами гиперболической геометрии, хотя они даже не слышали друг о друге и совершили открытие независимо друг от друга. Тому было несколько причин. Лобачевский писал только на русском языке, и его работы стали широко известны лишь через много лет после его смерти. Однако в настоящее время гиперболическая геометрия чаще всего ассоциируется именно с ним. В 1868 году итальянский математик Бельтрами изучил вогнутую поверхность, называемую псевдосферой, и доказал, что на этой поверхности работает геометрия Лобачевского! 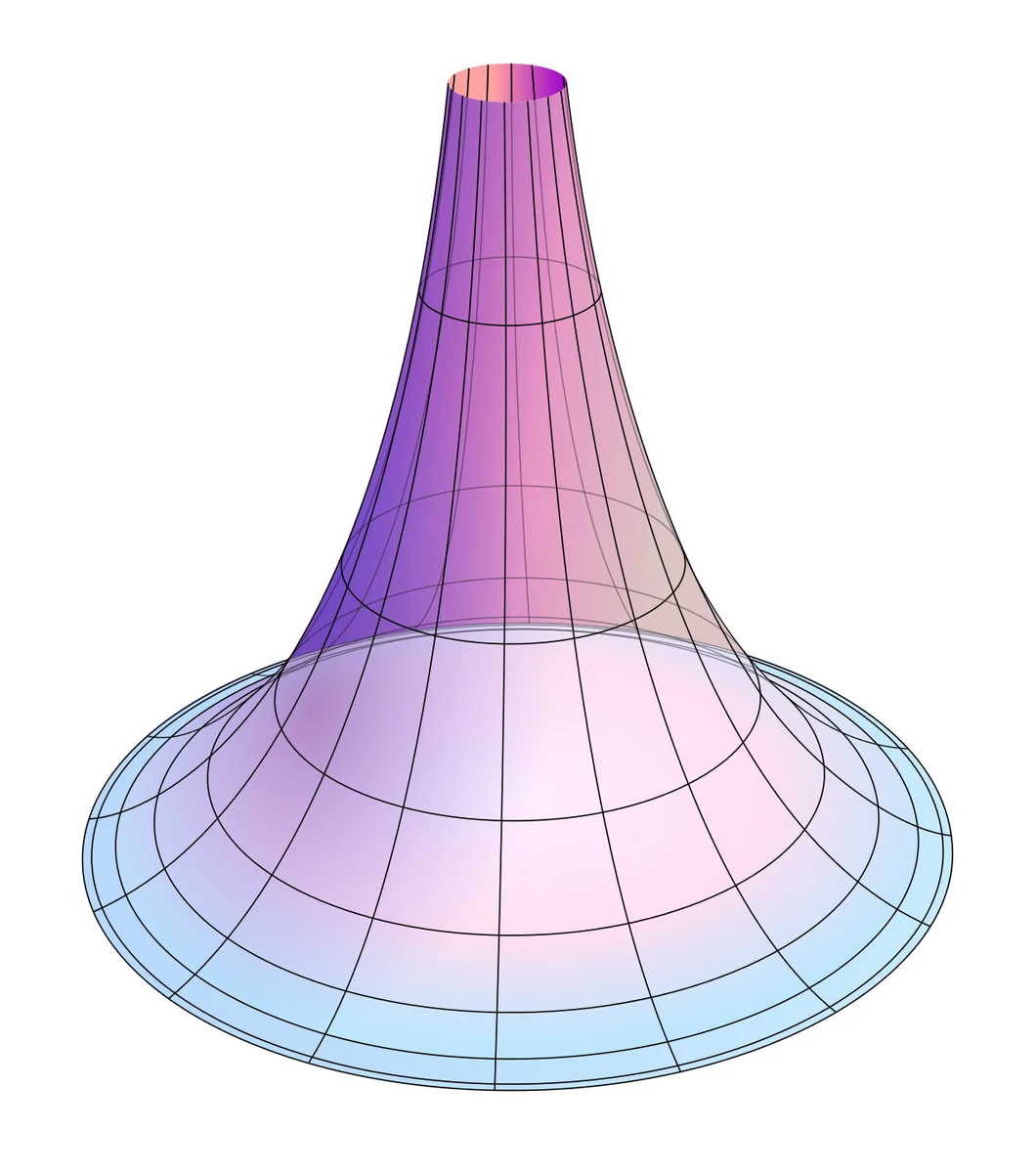 Если провести на этой поверхности кратчайшие линии и по этим линиям измерить расстояние, сделать из дуг этих линий треугольники и т. Д., То окажется, что все формулы геометрии Лобачевского могут быть реализованы (в частности, сумма углы любого треугольника меньше 180°). Впоследствии появились и другие модели геометрии Лобачевского. Эти модели окончательно установили, что геометрия Лобачевского не противоречива. Таким образом, было показано, что евклидова геометрия не единственно возможная. Это оказало большое прогрессивное влияние на все дальнейшее развитие геометрии и математики в целом. А в XX веке было обнаружено, что геометрия Лобачевского важна не только для абстрактной математики как одна из возможных геометрий, но и имеет прямое отношение к приложениям математики в физике. Выяснилось, что отношения пространства и времени, описанные в специальной теории относительности, напрямую связаны с геометрией Лобачевского. Например, формулы геометрии Лобачевского используются при разработке синхрофазотрона. ДРУГИЕ НАУЧНЫЕ ДОСТИЖЕНИЯ Лобачевский получил ряд ценных результатов и в других разделах математики: так, в алгебре он разработал, независимо от Ж. Данделена, метод приближённого решения уравнений, в математическом анализе получил ряд тонких теорем о тригонометрических рядах, уточнил понятие непрерывной функции, дал признак сходимости рядов и др. В разные годы он опубликовал несколько содержательных статей по алгебре, теории вероятностей, механике, физике, астрономии и проблемам образования. |
