практика. практика (2). Геометризация месторождений полезных ископаемых при их разведке и разработке

• Название: Геометризация месторождений полезных ископаемых при их разведке и разработке
• Анкор: практика
• Дата: 09.04.2023
• Размер: 308.09 Kb.
• Имя файла: практика (2).docx
• Тип: Документы; #1048817
• страница: 2 из 3

Проекции с числовыми отметками. Сущность метода проекций с числовыми отметками заключается в том, что на некоторую плоскость, называемую плоскостью проекций, ортогонально проектируются точки, принадлежащие некоторым элементам или пространственному телу. На плоскости проекций получают изображение проектируемых элементов или тела в двух измерениях. Третьим измерением являются числовые отметки точек.

Числовой отметкойназывают расстояние по нормали от проектируемой точки до плоскости проекций. За основную плоскость проекций в практике чаще всего применяется горизонтальная.

На рис.6 показано изображение точек в проекциях с числовыми отметками. В пространстве взяты произвольные точки А и В и горизонтальная плоскость Н. Точка С взята на плоскости и ее числовая отметка равна нулю. Проекции точки 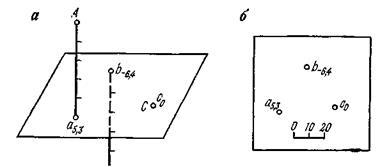  , В провести перпендикулярные к плоскости линии до пересечения с ней, то получим прямоугольные проекции точек а, b на плоскости Н. Нетрудно видеть, что точка С совпадает со своей проекцией с₀, и лежит на плоскости проекции. Числовые отметки точек, расположенных над плоскостью проекций, считаются положительными, ниже плоскости -отрицательными. Знак минус пишется только у отрицательных числовых отметок.



Рис.6. Проецирование точек на горизонтальную плоскость проекций:

а - точки А и В расположены вне плоскости проекций ; б - точка С на плане.

Часто некоторые объекты проецируются на вертикальную плоскость V (рис.7). На рис. 7 показан способ проецирования точек Д и Е на вертикальную плоскость. При этом отрицательные отметки имеют точки, расположенные за плоскостью 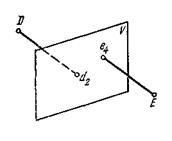проекций.

Проецирование точек на вертикальную плоскость проекций.

Если горизонтальную или вертикальную плоскости проекций принимают за любую условную плоскость, то числовые отметки называют условными отметками(относительными).

Проекции точек и прямых линий.В практике часто некоторые выработки принимают за точку и прямую линию. Это скважины и горных выработки, линии простирания и падения залежей полезного ископаемого, горных пород и другие.

Отрезок прямой на плане в проекциях с числовыми отметками может быть задан координатами двух точек а_16,2 и в_48,2 прямой (ав) (рис. 8,а), координатами одной точки с_10,5 и направлением прямой под дирекционным углом α (рис. 8,6) и углом падения прямой β (рис. 8,в).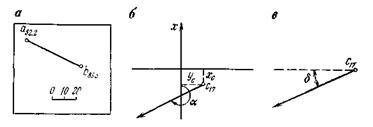



Рис. 8. Изображение отрезка прямой линии в проекциях с числовыми отметками.

Углом направления α прямой называется угол между северным направлением оси х и направлением прямой в сторону ее понижения, отсчитываемый по ходу часовой стрелки. Углом наклона β называется угол падения прямой к горизонту. В зависимости от знака угла наклона различают угол восстания (+β) и угол падения (-β) . Углы восстания и падения численно равны. На рис. 9 показана прямая АВ. Отрезок СВ этой прямой имеет угол падения δ, а отрезок СА этой же прямой - угол восстания, равный также δ.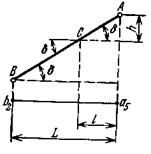



Рис. 9. К определению угла наклона прямой

Тангенс угла наклона прямой называется уклоном прямой, т.е.   . Проекция прямой на горизонтальную плоскость Н между двумя точками называется заложением l.

При решении различного характера задач в геологии, маркшейдерии и горном деле пользуются уклоном прямой, заложением и высотой сечения h этой прямой.

Градуированием прямойназывается определение на проекции прямой точек с дискретными (или кратными) числами, равные высоте сечения. Например, кратными числами могут быть 0,5, 1, 2,5 м и т.д.

Градуирование прямой может быть выполнено на глаз, с помощью трафарета или аналитическими способами. Аналитический способ градуирования прямой заключается в следующем: Пусть на рис. 10 дан в плане отрезок a₁₆b₂₅.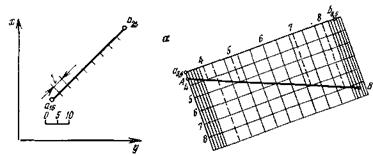



Рис. 10. Аналитический способ градуирования прямой

Требуется этот отрезок проградуировать при h=1м. Допустим, что длина отрезка a₁₆b₂₅ (горизонтальное положение) составляет 36мм. Величина заложения l на 1 м превышения определяется из соотношения:



Отсюда:     

Тогда отрезком в 4 мм и градуируется прямая a₁₆b₂₅. Если данные точки имеют дробные или некратные заданному числу отметки, то предварительно находят на прямой точку с целыми или кратными величине h числовыми отметками.

Графический способ градуирования может быть выполнен двумя способами: способ профиля и способ трафарета.

Способ профиля (рис.11,а). Градуирование указанным способом проводится с помощью миллиметровой бумаги. Отрезок прямой a_3,4b_8,5 необходимо проградуировать через 1 м.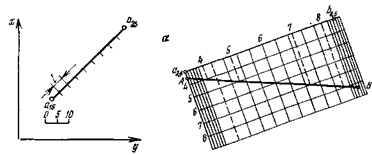



 Графический способ градуирования прямой: а- способом профиля; б- способом трафарета.

 

Способ трафарета (палетки) (рис.11,б). На кальке или на прозрачной бумаге строят трафарет (или палетку), т.е. проводят ряд параллельных линий на одинаковом расстоянии. Расписывают палетку через заданную высоту сечения h=1 м. Накладывают ее на данный отрезок (а_12,6в_19,5) таким образом, чтобы отметка точки а_12,6 на плане совпадала с отметкой на палетке. Закрепляют палетку иголкой в точке а_12,6 и вращают ее до тех пор, пока она не займет положение, при котором отметка точки в₁₉ на плане будет соответствовать такой же отметке на палетке. Закрепляют палетку в таком положении и, приложив к линии линейку, делают легкие наколы точек пересечения линии палетки с отрезком a_12,6b_19,5 (точки 14,16,18 м). Снимают палетку, и у точек накола выписывают отметки соответствующих линий палетки.

Взаимное положение прямых.Две прямые в пространстве могут пересекаться,скрещиваться, быть параллельными.

Прямые параллельнымежду собой, если параллельны их проекции, заложения равны, числовые отметки возрастают в одну сторону (рис. 12,а).

Прямые пересекаются,если пересекаются их проекции, а точка пересечения К_17,5 для обеих прямых имеет одну и ту же числовую отметку (рис. 12,б).

Прямые скрещиваются, если проекции прямых пересекаются, но в точке пересечения имеют разные отметки; проекции прямых параллельны, но имеют разные заложения, или имеют одинаковое заложение, но возрастание отметок идет в разные стороны (рис. 12,в).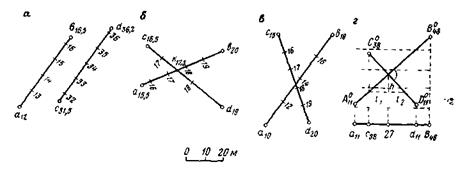



Рис. 12. Взаимное положение прямых.

Взаимное положение плоскостей.Плоскость в пространстве и ее изображение на плане может быть определена следующими элементами:

1) тремя точками, не лежащими на одной прямой;

2) прямой линией и точкой, находящейся вне этой прямой;

3) двумя пересекающимися прямыми;

4) двумя паралле льными прямыми.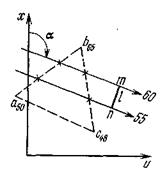



Плоскость может быть изобрежена в горизонталях (рис.13).

Плоскости в пространстве могут пересекаться и быть параллельными.

Пересекающиеся плоскости.Две плоскости пересекаются в пространстве, если соблюдается одно из следующих условий: а) одноименные горизонтали обеих плоскостей пересекаются; б) горизонтали заданных плоскостей параллельны и имеют противоположное направление; в) горизонтали заданных плоскостей параллельны, имеют одно направление, но заложения этих плоскостей неодинаковы по величине.

Пример 1: Пусть заданы две плоскости Р₁ и Р₂ (рис. 14). Определить линию пересечения плоскостей Р₁ и Р₂. и ее элементы залегания.

По заданным геометрическим элементам плоскости Р₁ и Р₂. изображают в проекциях с числовыми отметками в виде горизонталей (рис.14,а). Одноименные горизонтали плоскостей пересекаются в точках а и б. Соединив точки а и б, получим линию пересечения плоскостей Р₁ и Р₂. Графически измеряется угол простирания (   )линии пересечения.

Для определения угла падения строится вспомогательный разрез (рис.15,6). На разрезе по заложению d=аб линии пересечения и высоте сечения горизонталей h= 80-70=10 м.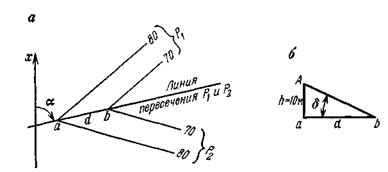



Рис.14. Построение линии пересечения двух плоскостей.

Пример 2: Пусть в проекциях с числовыми отметками заданы плоскости Р₁ и Р₂. (рис. 15,а). Горизонтали их пересекаются за пределами чертежа. Линию пересечения плоскостей Р₁ и Р₂ можно определить по способу вертикальных разрезов.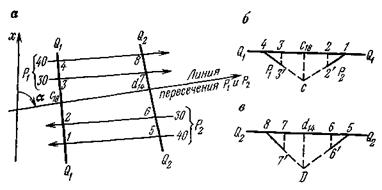



Рис. 15. Построение линии пересечения двух плоскостей при условии, если их одноименные горизонтали пересекаются за пределами чертежа

На рис.16 приведено решение аналогичной задачи, если горизонтали заданных плоскостей Р₁ и Р₂ направлены в одну сторону.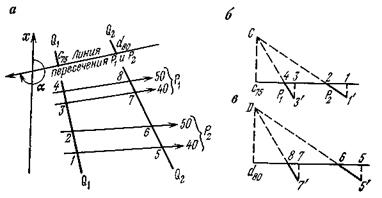



Рис. 16. Построение линии пересечения двух плоскостей при условии, что горизонтали направлены в одну сторону: а- план; б и в – вспомогательные разрезы.

Взаимное положение прямой и плоскости.Прямая линия и плоскость могут иметь следующее взаимное расположение: 1) прямая принадлежит плоскости; 2) прямая пересекает плоскость; 3) прямая параллельна плоскости.

Прямая принадлежит плоскости, если все три координаты двух ее точек совпадают с координатами точек заведомо принадлежащих плоскости (рис. 17,а).

Простирание прямой, расположенной в заданной плоскости, может иметь любое значение от 0 до 360°, а угол наклона прямой к горизонту может изменяться от 0° до 90⁰. В геолого-маркшейдерской часто встречаются различные виды задач.

Например: Пусть дана плоскость в проекциях с числовыми отметками и на ней прямая а₅в₂(рис. 17а,6). Определить угол наклона ab. Нетрудно видеть, что отрезок представляет собой заложение прямой ab на h=10 м. По заложению la и превышению h строится прямоугольный треугольник, в котором определяется угол наклона заданной прямой б (рис. 17,в).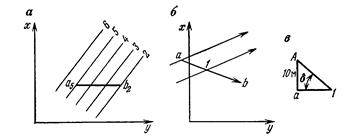



Рис.17.Прямая, принадлежащая плоскости.

Построение и получение сглаженных кривых содержания компонента по разведочной выработке

Параметры подсчёта запасов и способы их определения.

Общие формулы для подсчета запасов твердого ПИ в недрах следующие:

Q = S m_СР γ_СР, - количество полезного ископаемого,

Р = Q*c_CP*10^-2 – количество полезного компонента.

Величины, входящие в эти формулы, являются параметрами подсчета запасов.

S – площадь залежи или ее части, м²;

m_СР – средняя мощность залежи, м;

γ_СР – средняя объемная масса ПИ, т/м³;

c_CP – среднее содержание полезного компонента, %.

Подсчету запасов предшествует оконтуривание месторождений, разбивка его на блоки (определение границ залегания полезных ископаемых на плане или разрезе).

Внутренним контуром залежи называют линии, соединяющие крайние рудные скважины, встретившие полезные ископаемые.

Внешний контур – линия, соединяющая точки предполагаемой границы залежи.

Площадь залежи, заключенная между ними, называют междуконтурной полосой (рис. 6.1).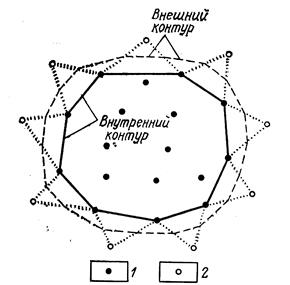



Внешний контур определяется интерполяцией на половину расстояния между крайними рудными и соседними безрудными скважинами. При отсутствии безрудных скважин этот контур может быть определен графически на вертикальных разрезах по углу выклинивания залежи в данном направлении. На плане изомощностей внешним контуром служит изолиния нулевой мощности.

 Рисунок 6.1 – Внутренний и внешний контур залежи, построенные интерполяцией на середину:

1 – рудные скважины; 2 – безрудные скважины.

Площадь при подсчете запасов определяется следующими способами: 1) планиметром (ошибка определения – около 3%); 2) графическим способом с разбивкой участка на простейшие фигуры; 3) с помощью палетки; 4) аналитически по координатам угловых точек участка:

S = 0,5 ∑ Y_n (X_n-1 – X_n+1) = 0,5 ∑ X_n (Y_n+1 – Y_n-1),

где n – порядковый номер вершины при обходе определяемого контура по часовой стрелке.

Определение средней мощности При равномерном распределении в пределах контура балансовых запасов точек, в которых измерена мощность залежи, среднее ее значение определяют как среднее арифметическое.

при большой изменчивости мощности, и особенно при неравномерном распределении точек замера, необходимо определять средневзвешенное значение из выражения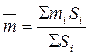



где m_i , S_i – численное значение измеренной мощности и площади, тяготеющей к i-й точке;

Для подсчета запасов берут полезную мощность, без прослоев.

Объемной массойγ полезного ископаемого называется масса единицы его объема в естественном состоянии. Определяется следующимиспособами:

Способ пробной вырубкиприменяется для слабых, трещиноватых, пористых и сильно загрязненных включениями залежей. В массиве ПИ вырубывается полость объемом V не менее 1 м³, из которой извлекается полезное ископаемое для взвешивания. Полученная полость тщательно измеряется для определения ее объема. Объемная масса определяется по формуле: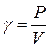



Лабораторный способприменяется для сравнительно плотных и однородных по составу полезных ископаемых. Образец весом около 300 г взвешивают (Р₁) на технических весах с точностью до ± 0,1 г. Затем его помещают в сосуд с водой и кипятят для насыщения водой. После охлаждения вновь взвешивают (Р₂). Затем насыщенный водой образец взвешивают в воде на гидростатических весах (Р₃).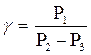



где Р₁ – вес образца до насыщения водой; Р₂ – после кипения; Р₃ – в воде.

 Аналитический способ применяется при наличии хорошо выраженной зависимости между γ и содержанием отдельных компонентов

γ = γ_o + k₁ A_C + k₂ S + k₃ W;

где γ_o – среднее значение объемной массы, определенное для конкретного шахтопласта, т/м³ (1,0 – 1,6);

k_i – коэффициенты, характеризующий изменение объемного веса при изменении золы, содержания серы, влаги на 1%; (могут изменяються в пределах 0,005 – 0,01).

А, S, W – среднее содержание внутренней золы, серы и влаги в массиве.

Например, для антрацитов Донбасса применима формула:

 ,

где А – внутренняя зольность угля;

W – пластовая влажность.