гидравлический расчет сифона. Гидравлический расчет. Гидравлический расчет сифонного трубопровода Содержание работы
 Скачать 370.09 Kb. Скачать 370.09 Kb.
|
|
Гидравлический расчет сифонного трубопровода Содержание работы 1. Теоретическая часть. Теоретические основы гидравлического расчета сложных трубопроводов и трубопроводов, работающих под вакуумом. 2. Расчетная часть. Сифонный трубопровод составлен из трех труб с заданными характеристиками Li, di, i (i = 1,2,3) и суммарными коэффициентами местных сопротивлений на i - том участке i; плотность ρ, вязкость керосина ν. Давление насыщенного пара при данной температуре pн.п. = 60 кПа. 1) Определить расходы Q1, Q2, Q3,используя графоаналитический метод. 2) Показать влияние на расходы увеличения температуры. 3) При какой температуре возможен максимальный расход? 4) Определить напор Н = z1 – z2 необходимый для того, чтобы обеспечить расход Q2= 5 л/с при закрытой задвижке на третьей трубе. Схема гидравлической системы 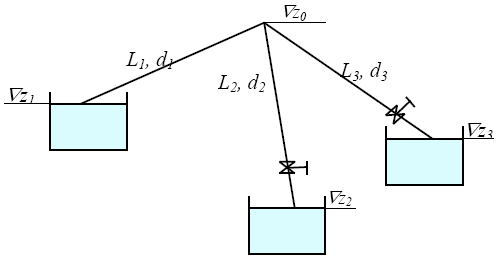 Решение. 1) Для обеспечения нормальной (бескавитационной) работы трубопровода должно выполнять условие pв0 ≤ pат – pн.п. = 100 – 60 = 40 кПа. Необходимый напор в наивысшей точке сифона  = = 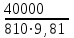 = 5,03 м. = 5,03 м.Принимаем в первом приближении квадратичную область сопротивлений, тогда коэффициенты гидравлического трения определим по формуле λ1 = 0,11 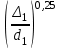 = 0,11 · = 0,11 · 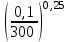 = 0,0149; = 0,0149;λ2 = 0,11 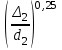 = 0,11 · = 0,11 · 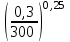 = 0,0196; = 0,0196;λ3 = 0,11 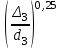 = 0,11 · = 0,11 · 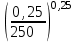 = 0,0196. = 0,0196.Так как z1 > z2 и z1 > z3, то жидкость из резервуара 1 перетекает в резервуары 2 и 3 Q1 = Q2 + Q3. (1) 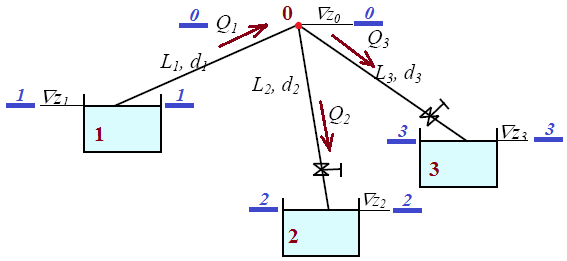 Решим задачу графоаналитическим способом. Для этого составим уравнения, связывающие между собой заданные напоры, напор в точке разветвления pв0/(ρg) и потери напора для каждой из трех труб, выраженные через расходы Q1, Q2 и Q3. Уравнение Бернулли для трубопровода 1 (сечения 1–1 и 0–0) z1 +  + + 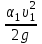 = z0 + = z0 +  + + 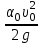 + Σhп1-0. + Σhп1-0.Для трубопровода 1: z1 = 3, z0 = 7; абсолютные давления в сечениях 1–1, 0–0 p1 = pат, p0 = pн.п. = 60 кПа; α1 ≈ α0 ≈ 0 (при турбулентном режиме). Потери напора Σhп1-0 = (1 + λ1 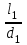 ) )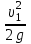 = (1 + λ1 = (1 + λ1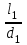 ) ) . .Получим уравнение z1 + 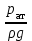 = z0 + = z0 + 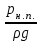 + (1 + λ1 + (1 + λ1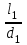 ) ) ; ; = z0 – z1 + (1 + λ1 = z0 – z1 + (1 + λ1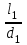 ) ) . (2) . (2)Уравнение Бернулли для трубопровода 2 (сечения 0–0 и 2–2) z0 +  + + 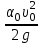 = z2 + = z2 + 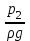 + + 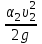 + Σhп0-2. + Σhп0-2.Для трубопровода 2: z0 = 7, z2 = 1; абсолютные давления в сечениях 0–0, 2–2 p0 = pн.п. = 60 кПа, p2 = pат; α0 ≈ α2 ≈ 0 (при турбулентном режиме). Потери напора Σhп0-2 = (2 + λ2  ) )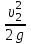 = (2 + λ2 = (2 + λ2 ) )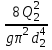 . .Получим уравнение z0 + 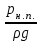 = z2 + = z2 + 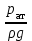 + (2 + λ2 + (2 + λ2 ) )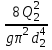 ; ; = z0 – z2 – (2 + λ2 = z0 – z2 – (2 + λ2 ) )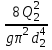 . (3) . (3)Уравнение Бернулли для трубопровода 3 (сечения 0–0 и 3–3) z0 +  + + 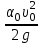 = z3 + = z3 + 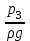 + + 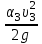 + Σhп0-3. + Σhп0-3.Для трубопровода 3: z0 = 7, z3 = 2; абсолютные давления в сечениях 0–0, 3–3 p0 = pн.п. = 60 кПа, p3 = pат; α0 ≈ α3 ≈ 0 (при турбулентном режиме). Потери напора Σhп0-3 = (3 + λ3 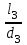 ) )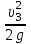 = (3 + λ3 = (3 + λ3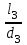 ) )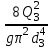 . .Получим уравнение z0 + 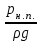 = z3 + = z3 + 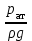 + (3 + λ3 + (3 + λ3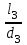 ) )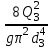 ; ; = z0 – z3 – (3 + λ3 = z0 – z3 – (3 + λ3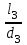 ) )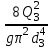 . (4) . (4)Тогда  = z0 – z1 + (1 + λ1 = z0 – z1 + (1 + λ1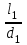 ) ) ; ; = z0 – z2 – (2 + λ2 = z0 – z2 – (2 + λ2 ) )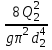 ; ; = z0 – z3 – (3 + λ3 = z0 – z3 – (3 + λ3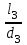 ) )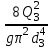 ; ;Q1 = Q2 + Q3. Построим кривые зависимости этого напора от расхода для каждой из трех труб
         3 B 2+3 2 1 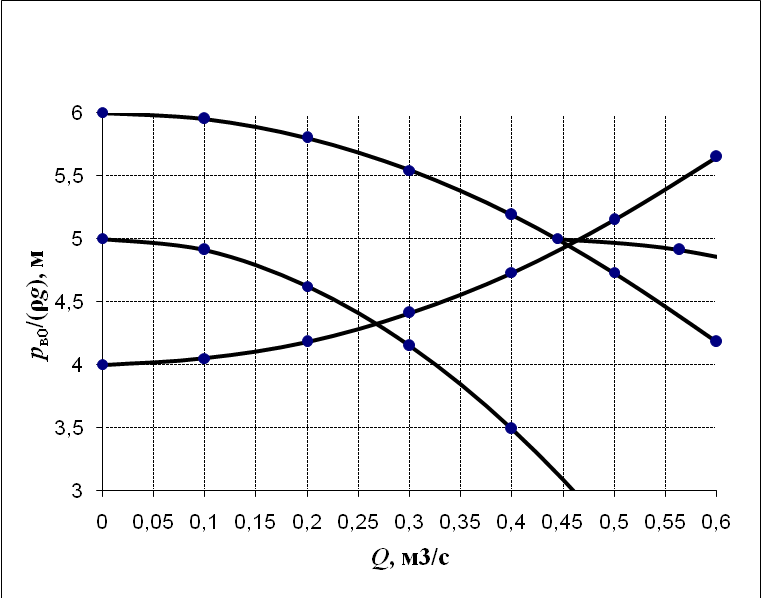 Строим кривую для ветвей, 1, 2 и 3. Ордината и абсцисса точки B пересечения суммарной кривой ветвей 3 и 2 с кривой ветви 1 дают соответственно действительный напор pв0/(ρg) = 5,01 м в узле 0 и расход Q1 = 0,47 м3/с, равный расходам Q2 + Q3 = 0,44 + 0,03 = 0,47 м3/с. Уточним зону сопротивлений. Найдем число Рейнольса Re1 = 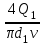 = =  = 997877; = 997877;Re2 = 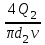 = = 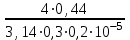 = 934183; = 934183;Re3 = 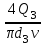 = = 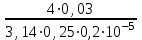 = 76433. = 76433.Режим течения турбулентный. Переходные числа Рейнольдса ReI(1) = 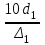 = = 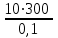 = 30000 < Re1 < ReII(1) = = 30000 < Re1 < ReII(1) = 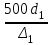 = = 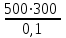 = 1500000; = 1500000;Re2 > ReII(2) = 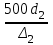 = = 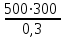 = 500000; = 500000;ReI(3) = 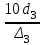 = = 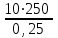 = 10000 < Re3 < ReII(3) = = 10000 < Re3 < ReII(3) = 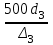 = = 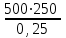 = 500000; = 500000;Коэффициенты гидравлического сопротивления по формуле Альтшуля (зона смешанного трения турбулентного режима) λ1 = 0,11 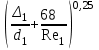 = 0,11 · = 0,11 · 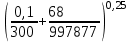 = 0,0156; = 0,0156;λ3 = 0,11 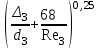 = 0,11 · = 0,11 · 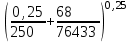 = 0,0229. = 0,0229.Уточним расходы
         3 B 2+3 2 1 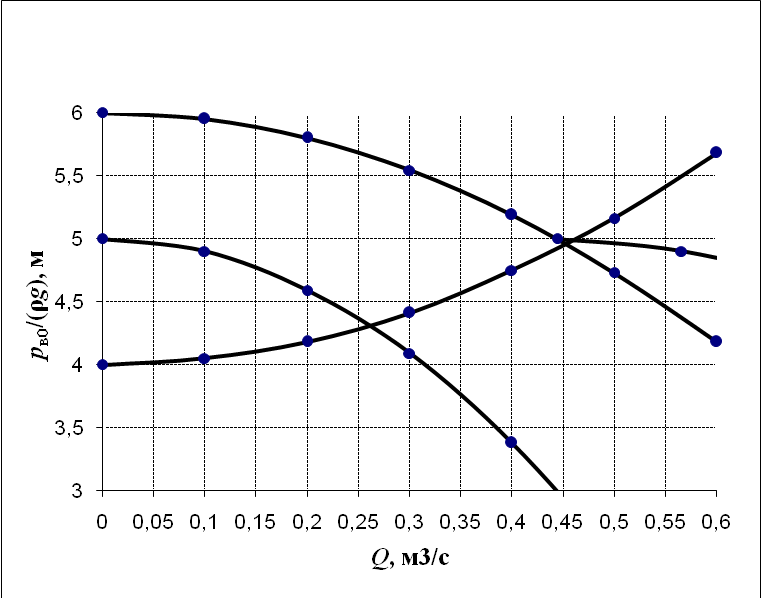 Строим кривую для ветвей, 1, 2 и 3. Ордината и абсцисса точки B пересечения суммарной кривой ветвей 3 и 2 с кривой ветви 1 дают соответственно действительный напор H = pв0/(ρg) = 5 м в узле 0 и расход Q1 = 0,46 м3/с, равный расходам Q2 + Q3 = 0,448 + 0,012 = 0,46 м3/с. Ответ: Q1 = 0,46 м3/с; Q2 = 0,448 м3/с; Q3 = 0,012 м3/с; H = 5 м. 2) Показать влияние на расходы увеличения температуры. Для ответа на второй вопрос воспользуемся графиком зависимости кинематического коэффициента вязкости нефтепродуктов от температуры. При увеличении температуры, кинематический коэффициент вязкости керосина уменьшается, принимаем уменьшение в два раза ν = 0,1 · 10-5, м2/с, тогда число Рейнольса Re1 = 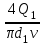 = =  = 1953291; = 1953291;Re2 = 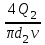 = = 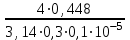 = 1902336; = 1902336;Re3 = 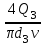 = = 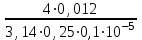 = 61147. = 61147.Режим течения турбулентный. 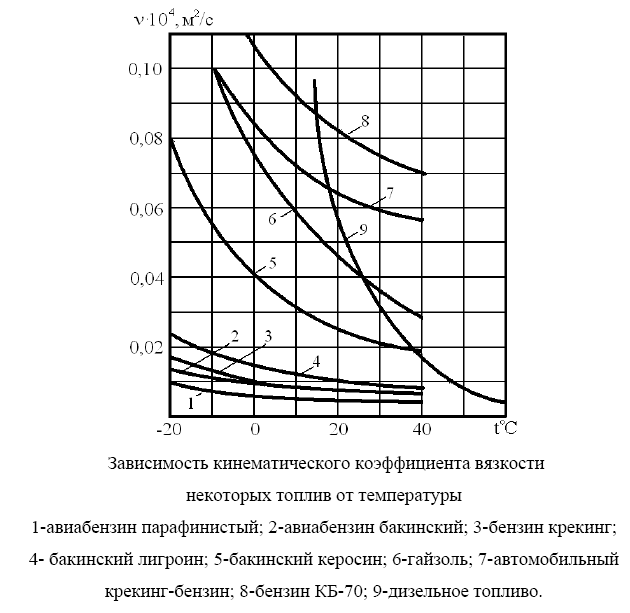 Переходные числа Рейнольдса Re1 > ReII(1) = 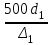 = = 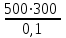 = 1500000; = 1500000;Re2 > ReII(2) = 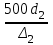 = = 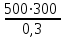 = 500000; = 500000;ReI(3) = 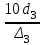 = = 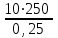 = 10000 < Re3 < ReII(3) = = 10000 < Re3 < ReII(3) = 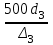 = = 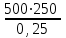 = 500000; = 500000;λ1 = 0,11 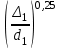 = 0,11 · = 0,11 · 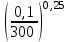 = 0,0149; = 0,0149;λ2 = 0,11 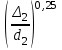 = 0,11 · = 0,11 · 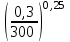 = 0,0196; = 0,0196;λ3 = 0,11 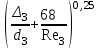 = 0,11 · = 0,11 · 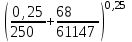 = 0,0236. = 0,0236.Определим расходы
         3 B 2+3 2 1 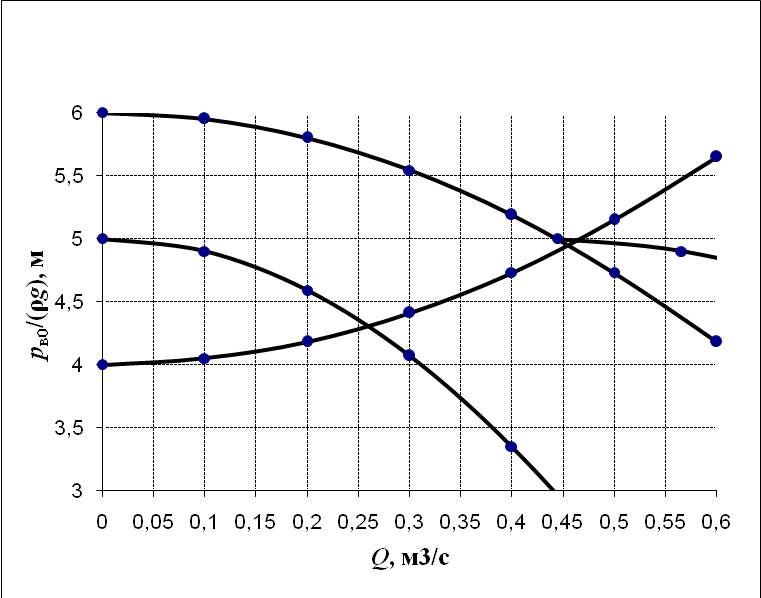 Q1 = 0,465 м3/с, равный расходам Q2 + Q3 = 0,446 + 0,019 = 0,465 м3/с. При увеличении температуры жидкости, вязкость уменьшается, потери напора становятся меньше и общий расход увеличивается. 3) При какой температуре возможен максимальный расход? Согласно графика зависимости кинематического коэффициента вязкости нефтепродуктов от температуры, максимальный расход керосина возможен при его температуре 40 °С, при такой температуре кинематический коэффициент вязкости керосина будет минимальный ν = 0,019 · 10-4, м2/с. 4) Определить напор Н = z1 – z2 необходимый для того, чтобы обеспечить расход Q2= 5 л/с при закрытой задвижке на третьей трубе. Так как d1 = d2 = 300 мм скорость движения жидкости υ = 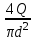 = = 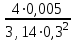 = 0,071 м/с. = 0,071 м/с.Число Рейнольса Re1,2 = 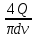 = = 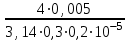 = 10616. = 10616.Режим течения турбулентный. Переходные числа Рейнольдса ReI(1) = 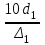 = = 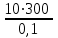 = 30000 > Re1; = 30000 > Re1;ReI(2) =  = = 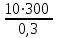 = 10000 < Re2 < ReII(2) = = 10000 < Re2 < ReII(2) = 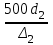 = = 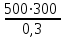 = 500000; = 500000;λ1 = 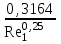 = = 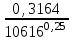 = 0,0312; = 0,0312;λ2 = 0,11 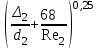 = 0,11 · = 0,11 · 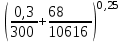 = 0,0323. = 0,0323.Составим уравнение Бернулли для сечений 1–1 и 2–2 z1 +  + + 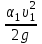 = z2 + = z2 + 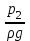 + + 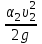 + Σhп1-2. + Σhп1-2.В рассматриваемом случае: z1 – z2 = Н; давление в сечениях 1–1 и 2–2 равно атмосферному p1 = p2 = pат; α1 ≈ α2 ≈ 0 (при турбулентном режиме); υ1 ≈ υ2 ≈ 0. Потери напора Σhп1-2 = (1 + λ1 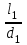 ) )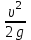 + (1 + λ2 + (1 + λ2 ) )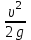 . .Получим уравнение Н = (1 + λ1 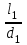 ) )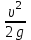 + (2 + λ2 + (2 + λ2 ) )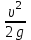 = = = (0,3 + 0,0312 · 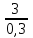 ) · ) · 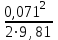 + (0,3 + 0,0323 · + (0,3 + 0,0323 · 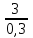 ) · ) · 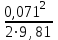 = 0,0003 м. = 0,0003 м.Список литературы Альтшуль А.Д., Киселев П.Г. Гидравлика и аэродинамика. М., Стройиздат, 1975. Арустамова Ц.Т., Иванников В.Г. Гидравлика, М., 1995. Астрахан И.М. Динамика вязких жидкостей (ньютоновских и неньютоновских). М., РГУ НГ, 2005. Астрахан И.М., Розенберг Г.Д. Механика неньютоновских жидкостей. М., РГУ НГ, 2000. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. «Нефтегазовая гидромеханика», М., Недра, 2005. Евгеньев А.Е. Гидравлический расчет сложных трубопроводов, М., МИНХ и ГП, 1975. Мищенко И.Т. Скважинная добыча нефти. М., РГУ НГ, 2003. Уилкинсон У.Л. Неньютоновские жидкости. М., Мир, 1964. Чугаев Р.Р. Гидравлика. Л., Энергоиздат, 1982. |
