Курсовая работа по гидравлике в нефтяной промышленности. КУРСОВАЯ РАБОТА Мухаметов А.У.. Гидравлика и нефтегазовая гидромеханика
 Скачать 268.67 Kb. Скачать 268.67 Kb.
|
|
Указания 1. Плотность жидкости определите с помощью Приложения 1, а момент инерции круга - по Приложению 2. 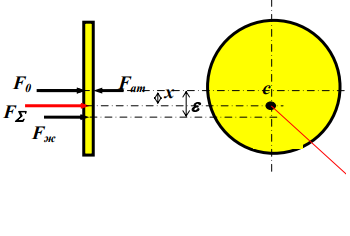 2. Схема сил, действующих на стенку АВ: 2. Схема сил, действующих на стенку АВ:F0 - сила внешнего давления; Fж - сила весового давления; Fат – сила атмосферного давления; FΣ - суммарная (равнодействую-щая) сила давления на стенку цистерны. Точка приложения силы давления FΣ (величина х определяется по теореме Вариньона) Таблица исходных данных
Решение: S – смоченная площадь стенки. 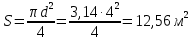 ; ;Плотность диз.топлива при t=35° определим по формуле: 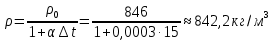 , ,где ρt - плотность жидкости при температуре t=t0 +Δt; Δt=35-20=15°С - изменение температуры; t0 - температура, при которой плотность жидкости равна ρ0; α - коэффициент температурного расширения, для диз.топлива α=0,0003 1/°С. Поскольку над поверхностью жидкости имеет место вакууметрическое давление р, создаваемое силой Fо, действующей на стенку, то в таком случае: 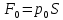 ; ; 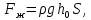 где h0 – глубина погружения центра тяжести от свободной поверхности жидкости; g – ускорение свободного падения, g=9,81 м/с2; 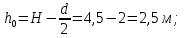 При давлении на поверхности жидкости меньше, чем атмосферное, получим суммарную силу давления на стенку цистерны: 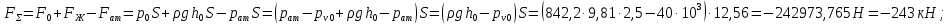 Момент инерции фигуры для нашего случая (окружность): 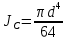 ; ;Координату точки приложения суммарной силы определим через пьезометрическую высоту: 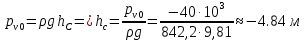 ; ;Знак минус означает, что на свободной поверхности присутствует вакууметрическое давление. Координата точки приложения силы относительно центра тяжести стенки по теореме Вариньона 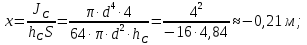 Относительно свободной поверхности: 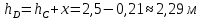 . .Ответ: FΣ= -243 кН; х=-0,21 м. Задача 7 (раздел 6). Сборник задач [1]. Для поддержания пластового давления при добыче нефти в нагнетательную скважину глубиной H по насосно-компрессорным трубам (диаметр d, длина l, шероховатость Δэ) закачивается Q м3 воды в сутки. Забойное избыточное давление равно рзаб. Температура воды t°C. Показание устьевого манометра рм. Определить расход воды. 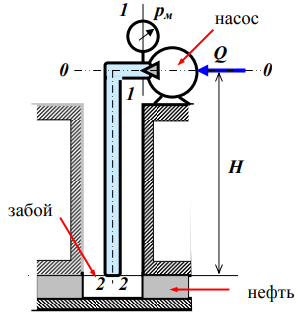 Рисунок 2 - к задаче 7 Таблица исходных данных Указания Примените уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0. При расчете потерь учтите только потери по длине. Местными потерями пренебречь. Принять длину трубопровода равной H.
Решение: Выбираем два сечения 1-1 и 2-2, а также плоскость сравнения 0-0 и записываем в общем виде уравнение Бернулли: 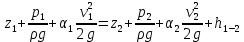 . .Здесь р1 и р2 – абсолютные давления в центрах тяжести сечений, Па; ϑ1 и ϑ2 – средние скорости в сечениях, м/с; z1 и z2 – высоты центров тяжести сечений относительно плоскости отсчета 0-0, м; h1-2 –потери напора при движении жидкости от первого до второго сечения, м. Определяем слагаемые уравнения Бернулли в данной задаче: Высоты центров тяжести сечений: z1 = 0; z2 =-H; Средние скорости в сечениях: 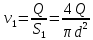 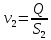 . .Так как площадь сечения 2-2 намного больше площади сечения 1-1 S2>>S1, то скорость изменения уровня воды в забое намного меньше скорости воды в трубопроводе ϑ1 << ϑ2 и можно принять , ϑ2=0. Коэффициенты Кориолиса α1 и α2 зависят от режима движения жидкости. При ламинарном режиме α=2, а при турбулентном α=1. Абсолютное давление в первом сечении р1 = рм + рат, рм – избыточное (манометрическое) давление в первом сечении, оно известно. Абсолютное давление в сечении 2-2 p2=pзаб + рат. Суммарные потери напора равны потерям напора по длине трубопровода (местными потерями напора пренебрегаем): 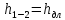 . .Потери по длине равны: 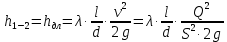 Итак, подставляем определенные выше величины в уравнение Бернулли и получаем закон сохранения энергии для нашей задачи: 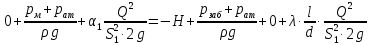 Сокращаем слагаемые с атмосферным давлением, убираем нули и приводим подобные члены, S1=S. В результате получим: 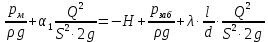 Приведём подобные: 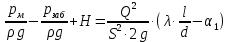 (1) (1)Это расчетное уравнение для определения расхода жидкости. Оно представляет собой закон сохранения энергии для данной задачи. Расход входит в правую часть уравнения непосредственно, а также в коэффициент трения λ через число Re. Не зная расход, невозможно определить режим движения жидкости и выбрать формулу для λ. Решим графоаналитическим способом. Задаёмся рядом значений расхода Q, вычисляя при каждом значении Q число Re, λ, f(Q), F(Q). В данном случае F(Q) обозначена левая часть уравнения (1). Число Рейнольдса: 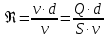 . .Re=2320 – критическое значение числа Рейнольдса. При Re<2320, 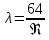 , α=2 – ламинарный режим. , α=2 – ламинарный режим.При Re>2320, 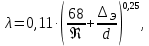 α=1 – турбулентный режим α=1 – турбулентный режимНайдем плотность при температуре 15°С (Приложение 1 – [1]): 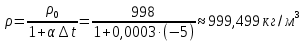 ; ;Кинематическая вязкость при определенной температуре определяется по формуле 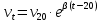 , ,где, ν20- вязкость при t=20°; 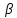 определяется по формуле определяется по формуле 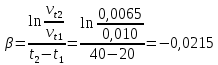 Отсюда вязкость при t=15°: 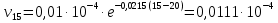 Найдем левую часть уравнения (1): 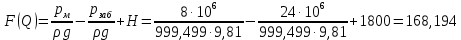 . .Подстановкой переменной Q, найдем правую часть уравнения (1): Задаемся Q=0,1 м3/час: 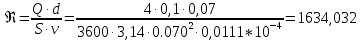 Примем длину трубопровода l=H. Так как Re<2320, 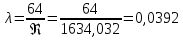 , α=2: , α=2: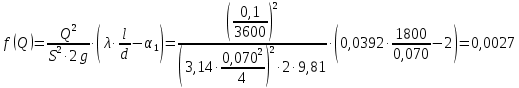 Q=5 м3/час: 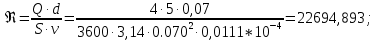 Так как Re>2320, 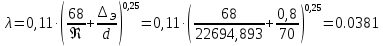 α=1: α=1: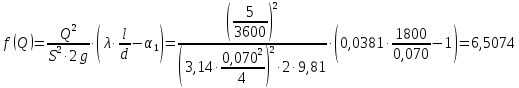 Расчеты и построение графиков выполним на ЭВМ с помощью электронных таблиц (Microsoft Excel). Ниже представлена расчетная таблица и графики.
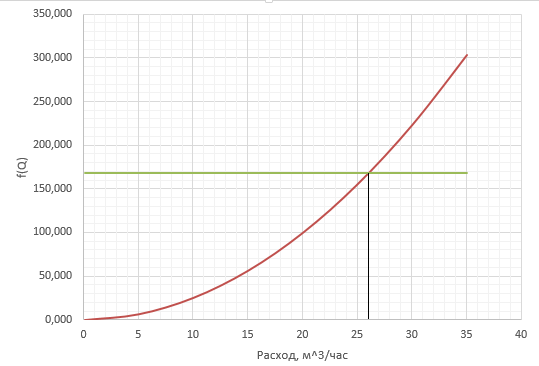  Рисунок 3 - гидравлическая характеристика простого трубопровода По графику определяем расход трубопровода: Q=26м3/ч=624м3/сут. Ответ: расход составляет 624м3/сут. Задача № 17. Сборник задач [2]. Рассчитать промысловую систему, указанную на схеме, состоящую из трех разводящий линий L1, d1, L2, d2, L3, d3, нагнетательной линии насоса L0, d0. В конечных пунктах заданы давления, р1, р2, р3и уровни жидкости в резервуарах z1, z2, z3. Даны физические свойства жидкости ν, ρ. Дано давление на выходе из насоса р0. Все трубы стальные бесшовные новые, расположены в одной горизонтальной плоскости. Определить расходы в ветвях и расход в нагнетательной линии насоса, а также давление в узловой точке А. 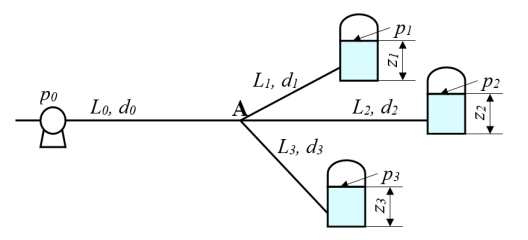 Рисунок 4 - к задаче 17 Исходные данные:
Δэ=0,014 мм | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
