гидравлика ответы. Гидравликалы жне пневматикалы жйелер пні бойынша емтихан сратары

• Название: Гидравликалы жне пневматикалы жйелер пні бойынша емтихан сратары
• Дата: 11.05.2023
• Размер: 1.35 Mb.
• Имя файла: гидравлика ответы.docx
• Тип: Документы; #1121217
• страница: 1 из 3

«Гидравликалық және пневматикалық жүйелер» пәні бойынша

емтихан сұрақтары

1. 
   Сұйықтықтың негізгі қасиеттері
   

Гидравликаның зерттеу объектісі - сұйық, табиғатта сұйықтың 4 агрегатты жағдайын қарастырады: қатты, сұйық, газ түрінде және плазмалы болып бөлінеді. Сұйық дегеніміз, қатты дене мен газ аралығында болады. Сұйықтың негізгі қасиеті - өте төменгі температура мен жоғары қысым кезінде, қатты дене қасиетінде болады (мұз), ал өте жоғары температура мен ең төменгі қысым кезінде - газ түріндегі қасиетіне айналады (бу).

Сұйық - физикалық дене, оның бөлшектері өте қозғалғыш, аққыш келеді де, сыртқы күш әсерінен өзінің формасын өзгерте алатын қасиеті бар. Сұйықтар сығылатын (газ түрінде) және сығылмайтын немесе өте аз сығылатын (тамшылы) болып бөлінеді.



Сұйық қозғалысының заңдылығын зерттеуді жеңілдету үшін, идеалды (киялдағы) және (реалды) нақтылы сұйықтар деп екіге бөледі.

Идеалды (қиялдағы) – ол абсолютті қозғалмалы (яғни, тұтқырсыз сұйық), бұл сұйықта үйкеліс күші мен жанама кернеу күші болмайды да, температура артқан сайын кеңеймейді, сыртқы күш әсерінен оның өлшемі өзгермейді.

Идеал сұйықтың модельдерін қолдану гидромеханика мен инженерлік гидравликаның көптеген есептері мен мәселелерін шешуді жеңілдетіп, қазіргі кездегі математикалық аппараттарды қолдану арқылы қозғалыстағы сұйыққа зерттеу жүргізуге мүмкіндік береді.

Нақтылы сұйық – табиғатта кездесетін, сығымдылық және сығу мен созу күштеріне кедергі келтіретін қасиеттерге ие сұйықтық.

2. 
   Сұйықтықтың тұтқырлығы мен тығыздығы, оларды анықтауға арналған аспаптар
   

Сұйық денесінің массасының m көлеміне V қатынасын сұйықтықтың тығыздығы ρ(кг/м³)деп атайды.Біртекті сұйықтық үшін: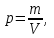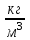

, (1.1)

мұндағы m-V көлеміндегі сұйықтықтың массасы.

Сұйықтық тығыздығы әртүрлі әдістермен анықталады. Өндірісте тығыздықты көп жағдайда арнаулы құрал ареометрмен өлшейді.

Сұйықтықтың тұтқырлығы – әртүрлі жылдамдықпен аққан сұйықтың екі қабатының арасында болатын үйкеліс кедергіні тұтқырлық деп атайды, немесе сұйықтың жанама кернеуге қарсы тұру қасиетін айтады, кейде сұйықтың ішкі үйкелісі деп те атайды. Сұйықтар тұтқырлықтарының шамасын анықтау үшін вискозиметр деп аталатын әртүрлі конструкциялы приборлар қолданылады.

3. 
   Гидростатикалық қысым және оның қасиеттері
   

Тыныштықта тұрған сұйықта сыртқы күштердің әсерінен сығу кернеуі пайда болады, ол гидростатикалық қысым деп аталады.

Сұйықтықтағы гидростатикалық қысым келесі қасиеттерге ие болады:

1) Гидростатикалық қысым өзі әсер ететін алаңшаға әрқашанда қалыпты нормаль бойынша бағытталады және әрқашан да қарастырылатын сұйықтың сыртқы бетінен ол сұйық көлемінің ішіне қарай бағытталады. Бұл қасиет тікелей қысымның анықтамасынан туындайды. Сұйықтықтың сыртқы беті деп сұйықтықтың газ тәріздес ортамен немесе қатты қабырғалармен жанасатын бетін ғана емес, сондай-ақ, сұйықтықтың жалпы көлемінен ойша бөлінетін элементар көлемдер беті деп түсінеміз.

2) Сұйықтық ішіндегі кез келген нүктеде гидростатикалық қысым барлық бағыттары бойынша бірдей әсер етіп, өзі әсер ететін алаңшаның көлбеулігіне тәуелсіз болады.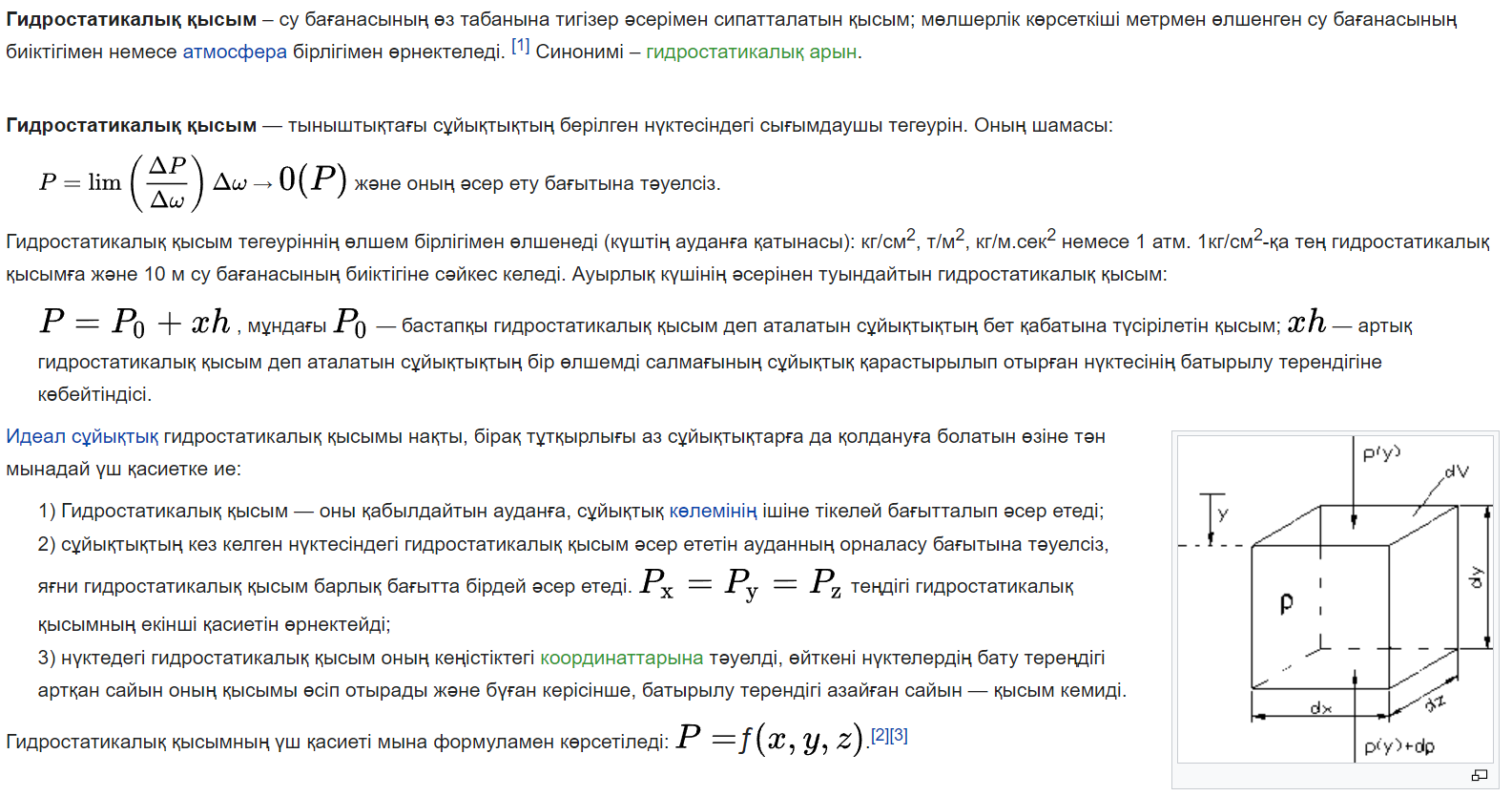

4. 
   Гидростатиканың негізгі теңдеуі
   

Гидростатиканың негізгі тендеуін қарастыратын болсақ - тыныштықтағы сұйықтықтың кез келген нүктесі үшін геометриялық және пьезометриялық қосындысы әрқашан тұрақты болады.

z + 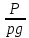= const
Осында: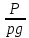

- пьезометриялық биіктік

P- сұйықтықтың ерікті нүктесіндегі гидростатикалық қысым

z- жоғары нүкте биіктігі

p- сұйық тығыздығы

g- ауырлық күші

z + P/γ = const.

z + P/γ қосындысы гидростатикалық арын деп аталады. Осылайша, гидростатикалық арын қозғалыссыз сұйықтықтың барлық көлемі үшін тұрақты шама болып табылады.

Осы формуланы басқаша да жазуға болады

p0+ 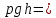const

I және II сұйықтық деңгейлері үшін теңдеу келесі түрде болады:



Теңдеу сұйықтықтың тыныштықтағы барлық нүктелеріндегі гидростатикалық басының тұрақты шама екенін көрсетеді.

Кейде Паскаль принципін гидростатиканың негізгі заңы деп те атайды.Паскаль заны осылай түсіндіріледі- сұйыққа немесе газға түсетін қысым барлық бағытта өзгермей кез келген нүктеге беріледі.

5. 
   Гидростатикалық қысымның түрлері. Қысымды өлшейтін құралдар.
   

Тыныштықта тұрған сұйықта сыртқы күштердің әсерінен сығу кернеуі пайда болады, ол гидростатикалық қысым деп аталады.

Сұйықтықтағы гидростатикалық қысым келесі қасиеттерге ие болады: 1) Гидростатикалық қысым өзі әсер ететін алаңшаға әрқашанда қалыпты нормаль бойынша бағытталады және әрқашан да қарастырылатын сұйықтың сыртқы бетінен ол сұйық көлемінің ішіне қарай бағытталады.

2) Сұйықтық ішіндегі кез келген нүктеде гидростатикалық қысым барлық бағыттары бойынша бірдей әсер етіп, өзі әсер ететін алаңшаның көлбеулігіне тәуелсіз болады.

Абсолютті нөлден есептелген қысым абсолютті қысым деп аталып, р_абс болып белгіленеді. Қысымның абсолютті нөлі сығылғыштық кернеудің жоқтығына сәйкес болады. Абсолютті немесе толық гидростатикалық қысымды (р) гидростатиканың негізгі теңдеуінен анықтайды: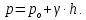
(2.11)
Абсолютті қысым р_абс мен атмосфералық қысымның р_а айырмасын артық немесе манометрлік қысым деп атайды: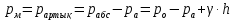
. (2.12)
мұндағы р_о - сыртқы қысым;

р_о = р_атм болғанда,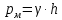
. (2.13)
Яғни, кез келген нүктенің бату тереңдігін сол нүктедегі манометрлік қысым анықтайды.

Толық қысымның атмосфералық қысымға жетіспеуін вакуум дейміз. Вакуумды қысымды келесі формуламен анықтаймыз: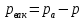
. (2.14)
Жоғарыда көрсетілген қысым түрлерін өлшейтін көптеген конструкциялы құралдар түрлері бар: сұйықтық, механикалық, құрамалы және т.б. Бұл құралдар абсолютті қысымды өлшемей, қысым айырымдарын өлшейді. Сондықтан бұл құралдарды - дифференциалды құралдар деп атайды. Мысалы: манометрлер толық және атмосфералық қысым айырымын, вакуумметрлер атмосфералық және толық қысым айырымын өлшейді.

Сынапты барометр (2.3-сурет) — бұл бір жағы ашық, екінші жағы сынап құйылған ыдысқа батырылған шыны түтік. Сынап бағанасы төмендеп, оның үстінен вакуум түзіледі. Сынап бағанасының төмендеуі, оның бетіне әсер ететін ауаның салмағымен (1) теңескенше жалғасады.

Манометрлік қысымды өлшейтін қарапайым құралдардың бірі - пьезометр. Пьезометр - ішкі диаметрі 5–12 мм, миллиметрде бөліктенген өлшеу шкаласының тақтайында орналасқан түтікше. Бұл түтіктің бір шеті сұйықтық құйылған сауытқа қосылады, ал екінші шеті ашық болады. Әдетте, пьезометрлер 30–40 кПа аспайтын қысым өлшеу үшін қолданылады, себебі үлкен шамадағы қысымды өлшеу үшін өте үлкен биіктіктегі түтікшелер орнату қажет болар еді.

Механикалық құралдар. Қысымды өлшейтін бұл құрал түрлеріне серіппелі және мембраналы манометрлер және вакуумметрлер жатады.

6. 
   Гидродинамика, сұйықтардың қозғалыс түрлері
   

1. 
   
   Гидродинамиканың негізгі түсініктері:
   

Гидродинамиканы үйренуде негізгі объектілердің бірі сұйық ағыны, яғни шекттеулі беттіктері арасынд

а сұйық массасының қозғалысы болып табылады.

Сұйық әр түрлі күштер әсерінен қозғалады: ауырлық күшінің; ішкі қысым; инерциялы күш және т.б.

Сұйықтың қозғалыс заңдарын оқып үйренуде екі түрлі есеппен түйісу керек болады:

1)сыртқы есеп, сұйық ағынының гидродинамикалық сипаттамалары көрсетілген, сұйықты айнала ағатын денеге салынған күшті табу керек.

2)ішкі есеп, сұйыққа әсерін тигізетін күштер берілген, ағынның гидродинамикалық сипаттамаларын табу керек.

Ағынның гидродинамикалық сипаттамалары болып:

-гидродинамикалық қысым;

-сұйық қозғалысының жылдамдығы.

Гидродинамикалық қысым -сұйықтың қозғалысы кезінде дамитын ішкі қысым.

Берілген нүктеде сұйық қозғалысының жылдамдығы -берілген нүктеде орналасқан, сұйық бөлшектерінің кеңістікте ауысу жылдамдығы. Жылдамдық бірлік уақыт ішінде сұйық бөлшегінің жүріп өткен жолының ұзындығымен анықталады.

 Сұйықтық қозғалысының режімдері мен түрлерінің классификациясы:

Сұйықтық ағысының екі режимі бар: ламинарлы, өтпелі және турбелентті.

Ламинарлы ағыс (қабаттық, реттелген) -сұйықтықтың жеке қабаттары бір-біріне қатысты араласпай жылжығандағы қозғалыс. Тұтқыр сұйықтықтар   (майлар) көбінесе реттеліп қозғалады.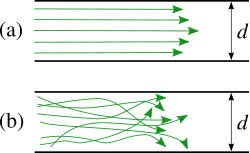 






Турбуленттік ағыс (реттелмеген) – сұйықтық бөлшектерінің әрдайым траекториясы өзгеріп тұратын және қарқынды араласу жүретін күрделі қозғалыс. Көбінесе тұтқырлығы аз сұйықтықтар (су, ауа) ретсіз қозғалады.

Құбырдағы сұйықтық ағынының күйі (режимі) тұтқырлық күшін сипаттайтын   шексіз Рейнольдс санына тәуелді, ол қозғалысты анықтайтын негізгі факторларды ескереді.

Рейнольдс саны келесі формуламен анықталады:

 , (3.1)

мұндағы  - ағынның сипаттық сызықтық өлшемі, м;

 - сұйықтықтың кинематикалық тұтқырлығы, м²/с;

 - сұйықтық қозғалысының жылдамдығы, м/с.

 Рейнольдс критикалық саны– қозғалыс ламинарлық режимнен турбуленттікке өтетін Рейнольдс санының мәні. Рейнольдс санының критикалық мәні сығылғын құбырларда артады және ұлғайған құбырда азаяды.

 >  - қозғалыстың турбуленттік режимі.

 <  - қозғалыстың ламинарлық режимі.

Дөңгелек ағысты құбырлар үшін   2000…2400; барлық көлденең ағыстар үшін   =500…600;ашық арналар үшін   =800…900.

Дөңгелек ағысты құбырлар үшін Рейнольдс саны келесі формуламен анықталады:

 . (3.2)

Барлық басқа көлденең ағыстар үшін (сонымен қатар ашық арналар үшін) Рейнольдс саны келесі формуламен анықталады:

 немесе  , (3.3)

мұндағы  - эквивалентті (гидравликалық) диаметр, м.

Сұйықтық қозғалысының бірнеше түрін атауға болады: орныққан және орнықпаған; бірқалыпты және бірқалыпсыз; арынды және арынсыз.

Орныққан қозғалыс -уақыт өтуіне байланысты кез келген нүктедегі ағын жылдамдығы мен гидродинамикалық қысым өзгермей, ал тек қана сұйықтық ағынындағы қарастырылып отырған нүкте орнына тәуелді, яғни оның координаталарының функциясы болып табылатын сұйықтық қозғалысы.

Мысалы, тұрақты арындағы резервуар саңылауынан сұйықтықтың ағуы, каналдағы өзгермейтін көлденең қималы және тұрақты тереңдіктегі су ағыны.

Орнықпаған қозғалыс -уақыт өтуіне байланысты әр нүктедегі ағын жылдамдығы мен қысымы өзгеретін сұйықтық қозғалысы.

Мысалы, айнымалы арын кезінде резервуар саңылауынан сұйықтық ағуы.

Бірқалыпты қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгермейтін сұйықтықтың орныққан қозғалысы.

Мысалы, өзгермейтін қималы және тұрақты тереңдіктегі құбыр немесе каналдағы сұйықтық қозғалысы.

Бірқалыпсыз қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгеретін сұйықтықтың орныққан қозғалысы.

Мысалы, конустық құбырда және табиғи арнадағы сұйықтықтың қозғалысы.

Арынды қозғалыс -құбыр өткізгіштің барлық көлденең қимасы атмосфералықтан жоғары қысыммен толтырылатын сұйықтық қозғалысы: сұйықтық қозғалысы қысым күштері арқасында жүзеге асады, яғни қосымша энергия шығынын тудырытын арын арқасында.

Арынсыз қозғалыс -атмосфералық қысымның астында орналасқан бос беті бар ағындағы сұйықтық қозғалысы.

7. 
   Ағынның гидравликалық сипаттамалары
   

Ағын режимі: Ламинарлы, Турбулентті

Ағын шығыны Q - t бірлік уақыт аралығында ω тірі қима арқылы өтетін V сұйықтықтың көлемі: Q=V/t,м^3/с

Ағынның орташа жылдамдығы υ – Q сұйықтық шығынының ω тірі қима ауданына қатынасымен анықталатын сұйықтықтың қозғалу жылдамдығы:

ϑ_орт=Q/ω,м/с

Ағынның гидравликалық радиусы R – тірі қиманың сулану (жұғу) периметріне қатынасы: R=ω/χ, м

Ағу сызығы (орнықпаған қозғалыс кезінде қолданылады) бұл әрбір нүктесінде берілген уақыт мезетіндегі жылдамдық векторы жанама бойынша бағытталған қисық.

Ағу түтігі – көлденең қимасы шексіз аз ағу сызықтары түзетін түтікшелі бет. Ағу түтігінің ішінде орналасқан ағын бөлігі элементар ағынша деп аталады.

8. 
   Идеал сұйықтыққа арналған Бернулли теңдеуі
   

1738 ж. Алынған Даниил Бернуллидің теңдеуі гидродинамиканың негізгі теңдеуі болып табылады. Ол ағынның әртүрлі қималарындағы қысым P, орташа жылдамдық υ пен пьезометрлік биіктік z арасындағы байланысты көрсетеді және қозғалыстағы сұйықтықтың энергиясының сақталу заңын өрнектейді. Осы теңдеудің көмегімен көптеген есептер шешіледі.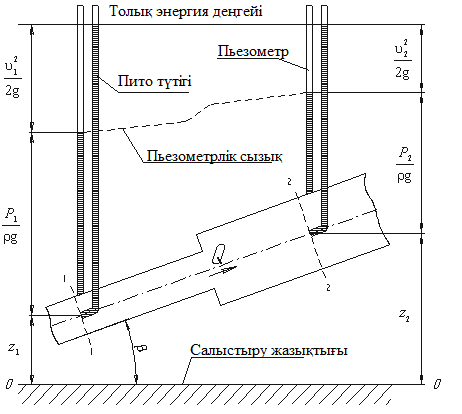



Егер Пито түтігіндегі сұйықтық деңгейлерінің көрсеткіші арқылы түзу жүргізсе, ол көлденең болады және құбыр өткізгіштің толық энергиясының деңгейін көрсететін болады.

Идеал сұйықтық ағынындағы ерікті таңдап алынған екі 1-1 және 2-2 қималары үшін Бернулли теңдеуі келесі түрде болады: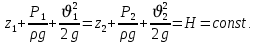


1-1және2-2 қималары еркімізше таңдап алынғандықтан, онда алынған теңдеуді басқаша жазуға болады: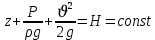


және былайша оқуға болады: идеал сұйықтық ағынының кез келген қимасы үшін Бернулли теңдеуінің үш мүшесінің қосындысы тұрақты шама болып табылады.

Энергетикалық тұрғыдан алып қарағанда теңдеудің әрбір мүшесі белгілі бір энергияның түрін білдіреді:

z₁ және z₂ - 1-1 және 2-2 қималарындағы потенциалдық энергияны сипаттайтын меншікті орналасу энергиясы;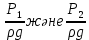

- дәл осы қималардағы қысымның потенциалдық энергиясын сипаттайтын меншікті қысым энергиясы;

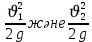- дәл осы қималардағы меншікті кинетикалық энергиялар.

Осыдан шығатыны, Бернулли теңдеуіне сәйкес кез келген қимадағы идеал сұйықтықтың толық меншікті энергиясы тұрақты.

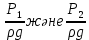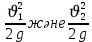Бернулли теңдеуін таза геометриялық тұрғыдан да түсіндіруге болады. Оның мәнісі теңдеудің әрбір мүшесінің сызықтық өлшемдері бар екендігінде. 3.5-суретке қарай отырып, z₁ және z₂ - 1-1 және 2-2 қималарының салыстырмалы жазықтықтан геометриялық биіктігі екенін; -пьезометрлік биіктіктер екенін; - көрсетілген қималардағы жылдамдық биіктіктері екенін көруге болады. Бұл жағдайда Бернулли теңдеуін былайша тұжырымдауға болады: идеал сұйықтық үшін геометриялық, пьезометрлік және жылдамдық биіктіктерінің қосындысы тұрақты шама.

9. 
   Нақты сұйықтықтың ағыншасына арналған Бернулли теңдеуі
   

Бернулли теңдеуі қозғалыстағы сұйықтың жылдамдығын,гидродинамикалық қысымын,ауырлық центрлерінің биіктік нүктерелерін z өзара байланыстыратын гидродинамиканың негізгі теңдеуі болып табылады.

Сұйықтықтың идеал ағыншасына қарағанда ішкі және сыртқы үйкеліс күштері ескеріледі де,соған сәйкес,ол осы күштерді жеңуге кететін энергия азаюмен ерекшеленеді.Энергияның бұл азаюларын арын азаюы деп атайды.

Әр түрлі кедергілерді жеңуге кететін механикалық энергия жойылып кетпей,жылулық энергияға түрленеді.Сөйтіп,энергияның сақталу заңы нақты сұйық үшін де өз күшінде қалады.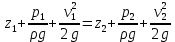