Теоретическая механика. Тест для подготовки к экз. по теор. мех.. Горизонтально
 Скачать 82.06 Kb. Скачать 82.06 Kb.
|
|
С1. Реакция цилиндрической шарнирно-неподвижной опоры А направлена: 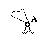 -произвольно в плоскости, перпендикулярной оси шарнира -горизонтально -вертикально -вдоль оси шарнира -произвольно в пространстве С2. Реакция цилиндрической шарнирно-подвижной опоры С направлена: 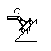 -в плоскости, перпендикулярной оси шарнира, перпендикулярно плоскости, на которой расположен шарнир -вдоль оси шарнира -вертикально -горизонтально -произвольно в плоскости, перпендикулярной оси шарнира С3. Реакция невесомой стержневой опоры СА направлена: 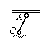 -вдоль стержня -вертикально -горизонтально -перпендикулярно оси стержня -произвольно в плоскости С4. Реакция гладкой опоры в точке С направлена: 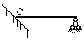 -перпендикулярно плоскости опоры -вдоль стержня -вертикально -горизонтально -перпендикулярно стержню С6. Момент в заделке А равен: 1 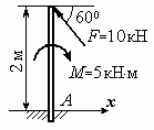 ) 10 кН·м; ) 10 кН·м;2) 5 кН·м; 3) 15 кН·м; 4) 2 кН·м; 5) 25 кН·м. С8. Жесткий стержень АВС в точке А опирается на шарнир, а в точке С – на гладкую поверхность, образующую угол 30° с горизонтом. При равновесии стержня реакция поверхности равна 12 Н, сила F при этом равна: 1 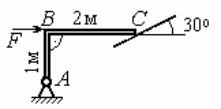 ) 36 Н; ) 36 Н;2) 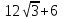 Н; Н;3) 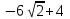 Н; Н;4) 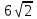 Н; Н;5) 25 Н. К6. Два шкива соединены ремённой передачей. Точка В одного из шкивов имеет скорость 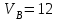 м/с. Скорость точки А другого шкива равна м/с. Скорость точки А другого шкива равна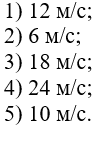 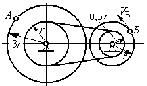 К13. Кривошип ОА планетарного механизма вращается с угловой скоростью = 2 рад/с. Определить скорость точки В, если радиус неподвижного колеса r = 0,2 м, а подвижного R = 0,4 м. 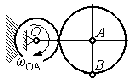  К15. Пластина вращается с постоянной угловой скоростью 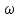 = 3 с–1 вокруг оси, перпендикулярной плоскости пластины. В пластину вписана половина окружности радиуса а = 0,4 м, по которой движется точка с постоянной скоростью V = 2 м/с. Найти величину проекции на ось Оу абсолютного ускорения точки в положении М, если b = 0,2 м. = 3 с–1 вокруг оси, перпендикулярной плоскости пластины. В пластину вписана половина окружности радиуса а = 0,4 м, по которой движется точка с постоянной скоростью V = 2 м/с. Найти величину проекции на ось Оу абсолютного ускорения точки в положении М, если b = 0,2 м.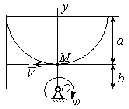 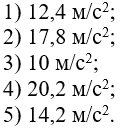 Д 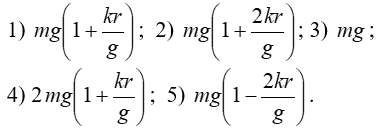 11. Груз массой m подвешен на нити, которая навивается на барабан согласно уравнению φ=k. t2. Определить натяжение нити, если радиус барабана r. 11. Груз массой m подвешен на нити, которая навивается на барабан согласно уравнению φ=k. t2. Определить натяжение нити, если радиус барабана r.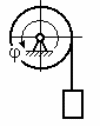 Д 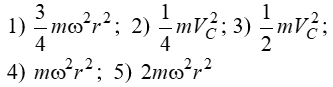 8. Диск массой m радиуса r м катится по горизонтальной поверхности с угловой скоростью ω. Определить кинетическую энергию диска. 8. Диск массой m радиуса r м катится по горизонтальной поверхности с угловой скоростью ω. Определить кинетическую энергию диска.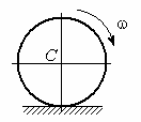 |
