инженерная графика. inzhenerka мин масштаб. Гост 302 соотношения 1 2, 1 2,5, 1 4, 1 5, 1 10 Вид
 Скачать 39.47 Kb. Скачать 39.47 Kb.
|
|
ГОСТ 2.301 – основные форматы A4-210*297, А3-297*420, А2-420*594, А1-594*841 Рамка- 20мм слева, остальные по 5мм Уголок- 185*55 ГОСТ 2.302- соотношения 1:2, 1:2,5, 1:4, 1:5, 1:10 Вид- это изображение на плоскости, обращенной к наблюдателю видимой частью предмета, полученное методом ортогонального проецирования ( 6 основных видов- 6 проекций) 5 4 1 3 6 2 Главный Сверху Слева Справа Снизу Сзади При выполнении черт. Вид сверху имеет преимущество перед видом снизу, а вид слева перед видом справа ГОСТ 2.304- шрифт Под углом в 45 град.! ТОЧКИ А’-(x;yП1) A”-(x;z) A”’-(z;yП3) ПРЯМЫЕ Для определения линии и пр-ве нужно знать 2 ее точки Прямые общего положения-пересекают все 3 пл-ти, 9 проекций следов, через 4 октант,3 следа Прямые частного п-я- 2 следа, 6 проекций Горизонталь- если прямая паралл. к пл-ти П1 Фронталь – это прямая, паралл. к пл-ти П2 Горизонтальная проекция горизонтали паралл. к ОХ, с фронталью тоже самое Частные случаи положения прямой: параллельные одной из плоскостей координат, перпендикулярные к одной из плоскостей координат, лежащие в плоскости координат, совпадающие с осью координат. Следом проекций называется точка пересечения заданных проекцией с плоскостью проекции. М- П1 A’B’-(N’ox, P’oy) N- П2 A”B”-(M”ox, P”oz) P- П3 A”’B”’-(M”’oy, N”’oz) ОПРЕДЕЛЕНИЕ ИНСТИННОЙ ПРЯМОЙ ПО ЕЕ ПРОЕКЦИИ При определении истинной длины отрезка методом трапеции, из концов ее проекций надо восстановить перпендикуляр и на них отложить значение недостающих координат, при этом перпендикуляр восстанавливают по одну сторону проекций, если знаки недостающих коорд. Одинаковы и наоборот, если разные При определении … методом треугольника, из данного конца проекции необходимо восстановить перпендикуляр и на этом перпендикуляре отложить алгебраическую разность недостающих координат точек А и В. Линия пересечения- это линия, которая принадлежит 2м плоскостям одновременно !!!Если прямая расположена в плоскости координат, то её проекция на эту плоскость совпадает с самой прямой, а две другие проекции совпадают с осями координат. Если прямая совпадает с осью координат, то две её проекции совпадают с самой прямой, а на плоскость, перпендикулярную этой оси, прямая спроецируется точкой в начало координат. - прямая, параллельная одной из плоскостей координат, имеет лишь два следа; - прямая, перпендикулярная к плоскости координат, имеет лишь один след; - два следа прямой совпадают в одной точке, если прямая пересекает ось координат; - три следа прямой совпадают, если прямая проходит через начало координат. ГОСТ 2.317 – проекции МЕТОДЫ ПРОЕЦИРОВАНИЯ Централльное - это проецирование на заданную плоскость из заданного полюса (центра) проецирования. Основные свойства : - любой геометрический элемент имеет на плоскости проекций единственную проекцию; - любая точка на плоскости проекций является проекцией бесчисленного множества точек (любой точки, расположенной на проецирующем луче); - проекцией прямой линии является прямая линия 2) Параллельное проецирование – проецирование с помощью параллельных проецирующих лучей, что наблюдается при бесконечном удалении полюса от плоскости проекций. 2.1 Косоугольные- аксонометрическая проекция, у которой направление проецирования неперпендикулярно к плоскости проецирования. Прямоугольные- это проецирование с помощью лучей, перпендикулярных к плоскости проекций Коэффициент искажения - отношение длины проекции отрезка оси на плоскость к его истинной длине. Аксонометрическая проекция- проекция на плоскость с помощью параллельных лучей, идущих из центра проецирования (который удален в бесконечность) через каждую точку объекта до пересечения с плоскостью, на которую проецируется объект. 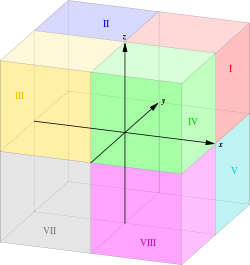 ОКТАНТЫ
Эпюр (эпюра) – чертёж, на котором пространственная фигура изображена методом ортогональных проекций на три плоскости ПЛОСКОСТЬ -это поверхность, обладающая тем св-вом, что прямая, проходящая через любые 2 точки этой пов-ти , лежит в ней всеми остальными точками Способы задания пл-ти: Равнозначными геометрическими элементами (3 точки, 2 пересекающ. Прямые, точка и прямая) Следами этой пл-ти Плоскими фигурами (частный случай) Плоскость общего положения- наклоненная ко всем плоскостям Плоскость частного положения- перпендикулярны каким-то плоскостям или параллельны Частные случаи положения плоскости: Перпендикулярные одной пл-тей координат- прецирующие Паралл. одной из пл-тей координат Проходящие через ось координат Проходящие через начало координат Случаи взаимного положения прямой и плоскости: Прямая лежит в пл-ти Пр-я паралл. пл-ти Пр-я перпендиклярна пл-ти Пр-я пересекает пл-ть Конкурирующие точки- это точки, принадлежащие разным геометрическим элементам, но у которых одна пара проекций совпадает Для того, чтобы определить какая из конкур. Точек находится ближе к наблюдателю, необходимо эти точки разнести на 2ой пл-ти проекций. Следом плоскости на данной плоскости координат называется линия пересечения плоскости с указанной плоскостью координат. |
