ььь. Графы. Поиск количества путей

• Название: Графы. Поиск количества путей
• Дата: 23.09.2022
• Размер: 1.47 Mb.
• Имя файла: ege13 (2).doc
• Тип: Документы; #691944
• страница: 2 из 7

Ещё пример задания:

Р-03. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М и проходящих через город В?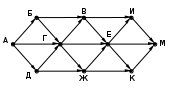



Решение:

1. 
   для того, чтобы оставить только маршруты, проходящие через вершину В, нужно представить граф в таком виде, «собрав его в пучок» около вершины В: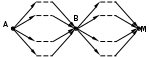
   

2. 
   проведём сечение графа через вершину В: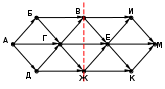
   

3. 
   обратим внимание на такой факт: если мы перешли через линию сечения из левой части в правую по ребру ГЕ или через вершину Ж, мы уже никак не попадём в вершину В (нет рёбер с «обратным направлением», поэтому эти маршруты запрещены; для более сложных случаев, когда такие рёбра с «обратным направлением» есть, нужно перерисовать граф (или провести сечение иначе) так, чтобы все вершины, ИЗ которых можно попасть в В, оказались слева от линии сечения
   
4. 
   в данном случае выбрасывается вершина Ж, все связанные с ней рёбра, и ребро ГЕ: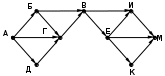
   

5. 
   дальше используем стандартный метод (см. разбор следующей задачи)
   
6. 
   покажем только окончательный результат: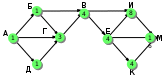
   

7. 
   Ответ: 16.
   

Ещё пример задания:

Р-02. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?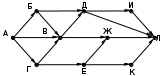



Решение:

1. 
   будем обозначать через N_X количество различных путей из города А в город X
   
2. 
   для города А есть только один маршрут – никуда не двигаться, поэтому N_A = 1
   
3. 
   для любого города X количество маршрутов N_X можно вычислить как
   

N_x = N_y + … + N_z

где сумма взята по всем вершинам, из которых есть прямой путь в вершину X; например,

N_Л = N_И + N_Ж + N_К

4. 
   около каждого города будем записывать количество маршрутов из А в этот город
   
5. 
   начнем считать количество путей с начала маршрута – с города А: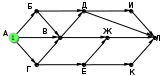
   

6. 
   теперь находим те вершины, в которые можно попасть напрямую из уже рассмотренных вершин (пока – только из А), это Б и Г, для них тоже количество путей равно 1: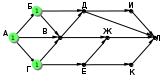
   

7. 
   теперь можно определить количество путей для В и Е; в В можно приехать только из А, Б и Г, а в Е – только из Г:
   

N_В = N_А + N_Б + N_Г = 1 + 1 + 1 = 3

N_Е = N_Г = 1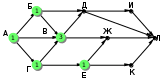

8. 
   теперь можно определить количество путей для Д, Ж и К; в Д можно приехать только из Б и В, в Ж – из В и Е, а в Е – только из Г:
   

N_Д = N_Б + N_В = 1 + 3 = 4

N_Ж = N_В + N_Е = 3 + 1 = 4

N_К = N_Е­ = 1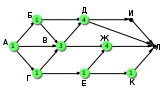

9. 
   теперь можно определить количество путей для И, куда можно приехать только из Д (N_И = N_Д) и, наконец, для Л:
   

N_Л = N_Д + N_И + N_Ж + N_К = 13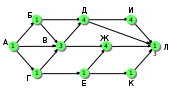

10. 
    Ответ: 13.
    

Ещё пример задания:

Р-01. Города A, B, C и D связаны дорогами. Известно, что существуют дороги между городами

A и С, C и B (две дороги), A и B, C и D (две дороги), B и D. Сколькими различными способами можно проехать из города А в город D, не заезжая дважды в один город?

Решение:

1. 
   нарисуем граф, в котором множественные дороги из одного города в другой будем обозначать одной дугой и подписывать около неё количество дорог: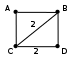
   

2. 
   выпишем все маршруты, по которым можно ехать из A в D так, чтобы дважды не проезжать один и тот же город:
   

   1 1	1 2	1 2 2	1 2 1
   A  B  D	A  С  D	A  B  С  D	A  C  B  D

3. 
   теперь рассмотрим маршрут A  B  D; на всех участках только одна дорога, поэтому есть только один такой маршрут
   
4. 
   для маршрута A  С  D: на первом участке только одна дорога, на втором – две, общее число маршрутов равно произведению этих чисел: 1*2 = 2
   
5. 
   аналогично находит количество различных путей по другим маршрутам
   

A  B  С  D: 1*2*2 = 4

A  C  B  D: 1*2*1 = 2

6. 
   всего получается 1 + 2 + 4 + 2 = 9.
   
7. 
   Ответ: 9.