ььь. Графы. Поиск количества путей
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
|
© К. Поляков, 2009-2021 13 (повышенный уровень, время – 3 мин)Тема: Графы. Поиск количества путей Что проверяется: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы). 1.3.1. Описание (информационная модель) реального объекта и процесса, соответствие описания объекту и целям описания. Схемы, таблицы, графики, формулы как описания. 1.2.1. Умение использовать готовые модели, оценивать их соответствие реальному объекту и целям моделирования. Что нужно знать: если в город R можно приехать только из городов X, Y, и Z, то число различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть где число путей конечно, если в графе нет циклов – замкнутых путей Пример задания:Р-05. (демо-2021) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город В? 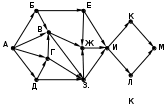 Решение: нас интересуют пути, проходящие через город В, поэтому на первом этапе отсекаем все ребра, которые позволяют на пути от А к М обойти город В; это рёбра БЕ, ГЗ и ДЗ; получается, что вершину Е тоже можно убрать, потому что в неё не ведёт ни одна стрелка; начальную вершину помечаем единицей (1 путь из А в А, никуда не ехать): 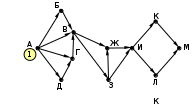 в вершины Б и Д можно ехать только из А, поэтому помечаем их тоже единицами; в вершину Г можно приехать из А (метка 1) и из Д, поэтому метка вершины Г – 2: 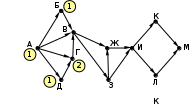 в вершину В можно приехать из Б (метка 1), А (метка 1) и Г (метка 2), так что метка вершины В равна 1 + 1 + 2 = 4: 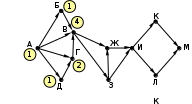 в вершину З можно ехать только из В, поэтому её метка тоже равна 4; для вершины Ж складываем метки В и З (4 + 4 = 8), а для И – складываем метки Ж и З (8 + 4 = 12) 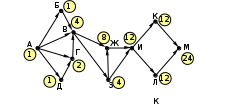 для вершин К и М получаем по 12 путей, а для М - 24 Ответ: 24. Решение (И.В. Степанов): нас интересуют пути, проходящие через город В, поэтому на первом этапе отсекаем все ребра, которые позволяют на пути от А к М обойти город В; это рёбра БЕ, ГЗ и ДЗ; получается, что вершину Е тоже можно убрать, потому что в неё не ведёт ни одна стрелка; 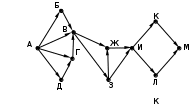 Рассмотрим все пути из А в В, просматривая вершины сверху вниз. Их всего 4: АБВ, АВ, АГВ и АДГВ. Теперь рассмотрим все пути из В в И (узловая точка через которую проходят все дороги в направлении М). Из В в И ведут 3 дороги: ВЖИ, ВЗЖИ, ВЗИ. Теперь остается определить дороги из и в М. Их 2: ИКМ и ИЛМ. Остается определить общее количество возможных путей. По правилу произведения комбинаторики N= 4*3*2=24. Ответ: 24. Ещё пример задания:Р-04. (Досрочный ЕГЭ-2020) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного пути из города А в город М? Длиной пути считать количество дорог, составляющих этот путь. 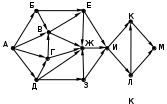 Решение: воспользуемся методом динамического программирования; индексом вершины назовем наибольшую длину пути из вершины А в эту вершину поступим почти так же, как и в рассмотренных ранее (ниже) задачах на вычисление количества маршрутов, но при определении индекса очередной вершины X вместо суммы индексов предыдущих вершин (как это было в задачах на количество путей) будем брать наибольшее шее из значений индексов предыдущих вершин + 1 у вершины А индекс 0, у тех вершин (Б и Д), в которые можно приехать только из А, индекс 0 + 1 = 1: 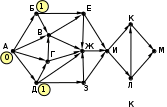 далее, у вершины З – индекс 1 + 1 = 2, у вершины Г: 1+max(0, 1) = 2, а у вершины В: 1+max(0, 1, 2) = 3 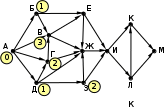 у вершины Е индекс 1+max(1,3) = 4, у вершины Ж – 1+max(1,2,3,4) = 5 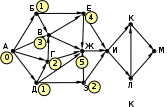 индекс вершины И: 1+max(2, 4, 5) = 6 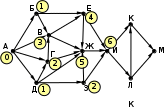 остается также поставить индексы остальных вершин 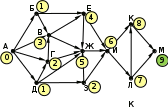 Ответ: 9. |
