Курсовая работа По дисциплине Оптимальные и адаптивные системы
 Скачать 193.39 Kb. Скачать 193.39 Kb.
|
|
Факультет информационных технологий Кафедра «Автоматическое управление» Курсовая работа По дисциплине «Оптимальные и адаптивные системы» Содержание Введение………………………………………………………………3 Оптимальные системы……………………………………………….4 Адаптивная система……………………………………………….....5 Синтез оптимальной эталонной модели методом динамического программирования с заданным функционалом оптимальности…...6-7 Синтез адаптивного регулятора с явной эталонной моделью……..8-10 Компьютерное моделирование……………………………………11-14 Заключение……………………………………………………………15 Список использованной литературы……………………..…………16 ВведениеРазвитие теории и практики построения САУ, ставят задачи построения систем управления, которые решали бы поставленные задачи наилучшим образом среди возможных в определенном смысле. Эти задачи известны, как задачи оптимального управления. При постановке задач оптимального управления, нужно правильно выбрать критерий оптимальности, который полностью отражает поставленную цель оптимизации также нужно обязательно правильно учесть ограничения на переменные состояния и на управляющие функции. Ограничения отражают конкретные конструктивные и энергетические особенности ОУ. Для решения задачи построения оптимального управления на сегодняшний день разработаны различные методы синтеза оптимального управления, при этом задачи синтеза решены более или менее только для линейных систем. При решении задач оптимального управления для нелинейных объектов задачи решены только для определенных классов. В соответствии с уровнем неопределенности этих непредвиденных изменении и задач управления адаптивные системы подразделяются на классы: Экстремальные адаптивные системы; Самонастраивающиеся системы; Самообучающиеся системы и другие. В данной работе рассматривается вопросы построения оптимально-адаптивной системы. При этом задача оптимизации решается на основе результатов теории динамического программирования, а задача адаптации строится в классе самонастраивающихся систем. Оптимальная системаОптимальная система- система автоматического управления, обеспечивающая наилучшее (оптимальное) с некоторой точки зрения функционирование управляемого объекта. Его характеристики и внешние возмущающие воздействия могут изменяться непредвиденным образом, но, как правило, при определённых ограничениях. Наилучшее функционирование системы управления характеризуется критерием оптимального управления (критерием оптимальности, целевой функцией), который представляет собой величину, определяющую эффективность достижения цели управления и зависящую от изменения во времени или в пространстве координат и параметров системы. Критерием оптимальности могут быть различные технические и экономические показатели функционирования объекта: КПД, быстродействие, среднее или максимальное отклонение параметров системы от заданных значений, себестоимость продукции, отдельные показатели качества продукции либо обобщённый показатель качества и т.п. Различают регулярный и статистический критерии оптимальности. Первый зависит от регулярных параметров и от координат управляемой и управляющей систем. Второй применяется тогда, когда входные сигналы — случайные функции или (и) нужно учесть случайные возмущения, порождённые отдельными элементами системы. Для проектирования оптимальной САУ необходима полная информация об ОУ, возмущающих и задающих воздействиях, начальном и конечном состояниях ОУ. Далее требуется выбрать критерий оптимальности. В качестве такого критерия можно использовать один из показателей качества системы. Однако требования к отдельным показателям качества, как правило, противоречивы (например, повышение точности системы достигается уменьшением запаса устойчивости). Кроме того, оптимальная система должна иметь минимально возможную ошибку не только при отработке какого-то конкретного управляющего воздействия, но в течение всего времени работы системы. Следует также учитывать, что решение задачи оптимального управления зависит не только от структуры системы, но и от параметров составляющих ее элементов. Оптимальное функционирование сложных объектов достигается при использовании самоприспосабливающихся (адаптивных) систем управления, которые обладают способностью автоматически изменять в процессе функционирования алгоритм управления, свои характеристики или структуру для сохранения неизменным критерия оптимальности при произвольно изменяющихся параметрах системы и условиях её работы. Поэтому в общем случае О. с. состоит из двух частей: постоянной (неизменной), включающей объект управления и некоторые элементы управляющей системы, и переменной (изменяемой), объединяющей остальные элементы. Адаптивные системыАдаптивные системы – это системы, которые автоматически приспосабливаются к изменению внешних условий и свойств объекта управления, обеспечивая при этом необходимое качество управления путем изменения структуры и параметров управляющего устройства. Примером изменяющихся внешних условий, требующих применения адаптивной САУ, являются нестационарные случайные внешние воздействия на систему, характеристики которых изменяются в широких пределах. В этих условиях точность работы САУ будет изменяться с изменением характеристик внешних воздействий. Для повышения точности системы необходимо изменять настройку корректирующих звеньев по мере изменения характеристик внешних воздействий. Эту перенастройку иногда может выполнять человек. В адаптивных САУ она осуществляется автоматически. Примером объекта с переменными параметрами, также требующего адаптивного управления, является самолет или ракета. Их динамические характеристики могут изменяться со временем в очень широких пределах вследствие изменения массы из-за уменьшения запаса горючего, изменения формы объекта или аэродинамических сил при изменении высоты и скорости полета. В этих случаях часто невозможно обеспечить автоматическое управление объектом во всех его режимах работы без изменения настройки или схемы управляющего устройства. Для автоматического выполнения этой задачи используются адаптивные САУ. Структурная схема адаптивной системы с эталонной моделью. Синтез оптимальной эталонной модели методом динамического программирования с заданным функционалом оптимальности.Адаптивная система с эталонной моделью. Задан объект управления, математическая модель которого представлена в виде: 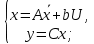 Где 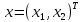 - вектор состояния, U-одномерная управляющая функция; y-одномерный выход объекта. - вектор состояния, U-одномерная управляющая функция; y-одномерный выход объекта.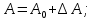 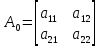 -заданная числовая матрица; -заданная числовая матрица;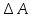 -матрица параметрических возмущений; -матрица параметрических возмущений;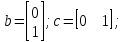 Эталонная модель задана уравнением: 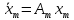 Идентификация матрицы параметрических возмущений ведется на основе метода наименьших квадратов. Эталонная модель определяется на основе оптимизации методом динамического программирования с функционалом оптимальности: 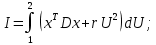 Где 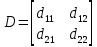 -заданная числовая матрица, элементы числовых матриц -заданная числовая матрица, элементы числовых матриц 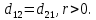 Вариант №13 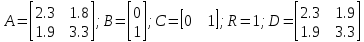 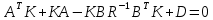 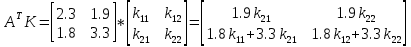 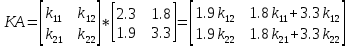 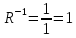 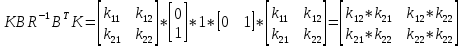 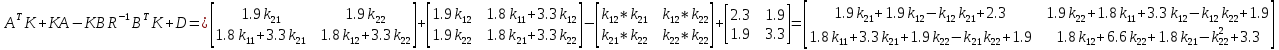 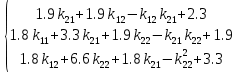 Найдем 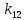 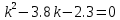 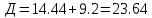 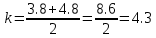 Найдем 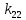 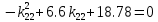 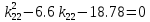 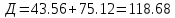 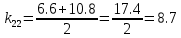 Найдем 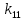 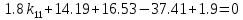 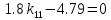 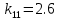 Итак матрица k выглядит следующим образом: 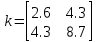 Синтез адаптивного регулятора с явной эталонной модельюТребуется найти адаптивный регулятор, который обеспечивает близость вектору, задаваемому эталонной моделью. Для адаптивных систем с эталонными моделями, синтез алгоритмов адаптации, в основном осуществляется на основе второго метода Ляпунова. Уравнение модели представляется в виде: xM=AMxM Это эталонная модель. Матрица Am определена в процессе синтеза оптимальной эталонной модели методом динамического программирования Белмана. 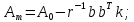 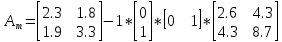 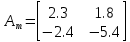 В связи с тем, что ОУ рассматривается, как линейный и модельный, закон регулирования ищется в классе линейных функций: 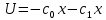 C1- матрица настраиваемых параметров, C0- числовая матрица, которая берется из условия согласования: 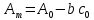 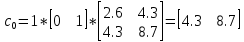 c1- находиться в виде дифференциальных уравнений. ẋ=Аx+∆Ax+Bu 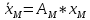 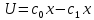 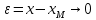 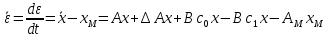 учитывая 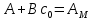 имеем имеем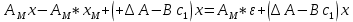 Берем функцию Ляпунова 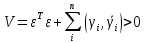 Где 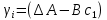 ; i-я строка матрицы ( ; i-я строка матрицы (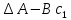 ) )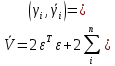 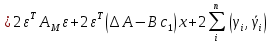 (*) (*)Попробуем, чтобы путем подбора 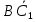 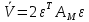 т.е. функция т.е. функция 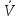 относительно относительно 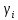 была бы нулевой, тогда по теореме Румянцева система будет устойчивой по части переменных, а именно по ɛ т.е. была бы нулевой, тогда по теореме Румянцева система будет устойчивой по части переменных, а именно по ɛ т.е. 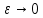 т.к. т.к. 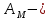 отрицательно определенная матрица, а по переменной отрицательно определенная матрица, а по переменной 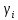 она она 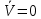 т.е. она не уходит в бесконечность т.е. она должна обеспечивать сходимость т.е. она не уходит в бесконечность т.е. она должна обеспечивать сходимостьПреобразуем в (*) второе и третье слагаемое 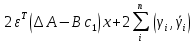 Здесь первое слагаемое 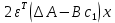 можно записать учитывая что можно записать учитывая что 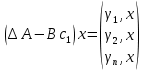 Итак 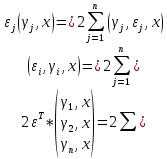 С учетом последнего выражения запишем 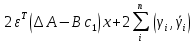 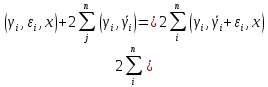 Подберем закон изменения 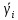 таким образом, чтобы таким образом, чтобы 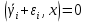 Потребуем чтобы 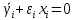 С учетом 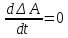 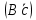 i= i=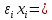 (x-xm)i (x-xm)i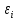 цц ццИтак, закон настройки : 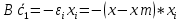 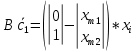 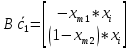 Компьютерное моделирование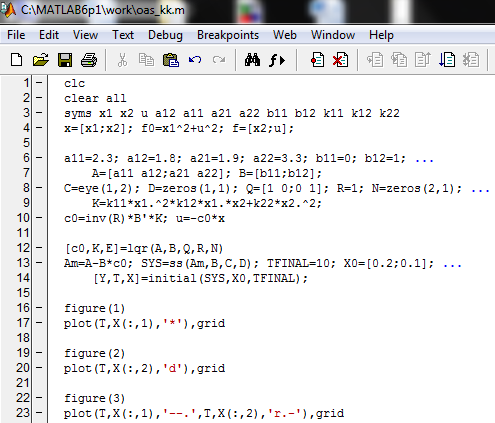 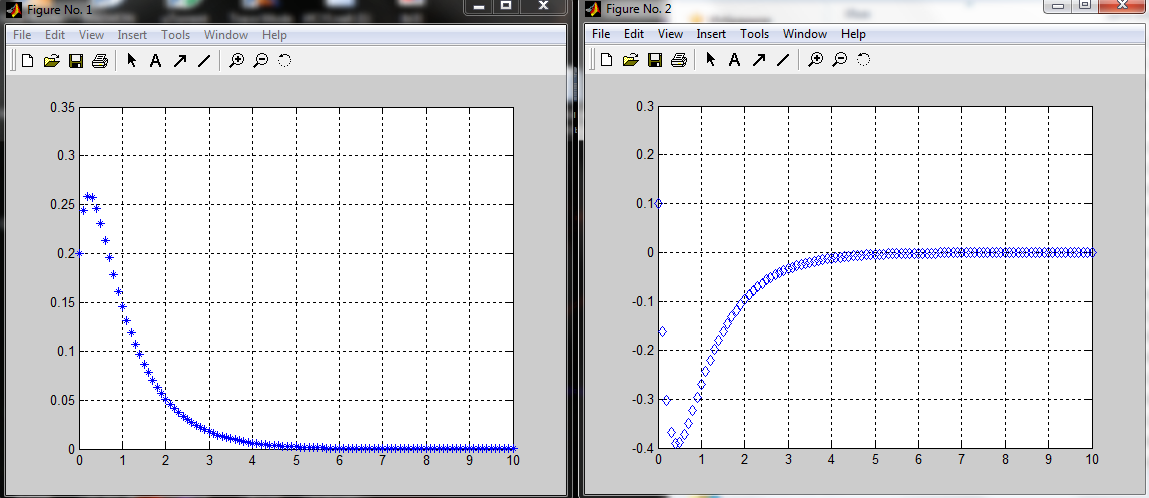 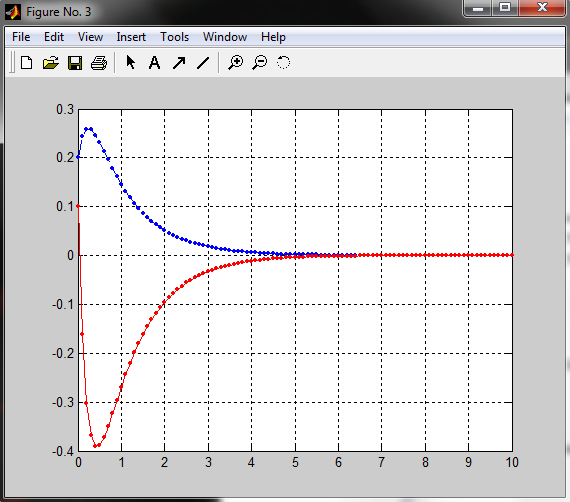 ЗаключениеТеория оптимального управления связано с требованиями к быстродействию и точности систем регулирования. Увеличение быстродействия возможно лишь при правильном распределении ресурсов управления, учет ограничений на управление стал одним из центральных в теории оптимального управления. Развитие теории адаптивного управления вызвано нарастающим количеством сложных объектов управления различной физической природы, параметры которых не определены. Причиной этой неопределенности могут являться: множество режимов работы объектов либо невозможность их экспериментального исследования с целью определения параметров без нарушения технологического процесса, наконец, сжатые сроки проектирования, не допускающие временных затрат на исследования и расчеты для определения параметров динамической модели объекта. В данной курсовой работе был проведен синтез оптимальной эталонной модели с помощью метода динамического программирования Белмана, а также синтез адаптивного регулятора с явной эталонной моделью. Дополнительно произвели компьютерное моделирование заданной системы. Список литературы |
