Лабораторная №2. Графы

• Название: Графы
• Анкор: Лабораторная №2
• Дата: 20.06.2022
• Размер: 33.93 Kb.
• Имя файла: lab2.docx
• Тип: Документы; #604701

Тема работы

Графы

Цель работы

Получить практические навыки представления графов в памяти ЭВМ, реализовать на языке программирования C/C++ алгоритмы работы с графами.

Задание

Используя алгоритм Дейкстры, найти кратчайший путь между двумя заданными вершинами во взвешенном неориентированном графе. Начальную и конечную вершины пути ввести с клавиатуры. Граф задать в текстовом файле матрицей весов.

Алгоритм решения

1. 
   Ввод n
   
2. 
   Выделение памяти для матрицы весов размером NxN
   
3. 
   Инициализация массива меток значением false
   
4. 
   Цикл для i = 0 .. n – 1
   
   1. 
      Цикл для j = 0 .. n – 1
      
      1. 
         Ввод a[i][j]
         
5. 
   Ввод начальной вершины и конечной вершин - st и last
   
6. 
   Выделение памяти для массива расстояний
   
7. 
   Положим d[st] = 0
   
8. 
   Цикл для j = 0 .. n – 1
   
   1. 
      Инициализация v значением -1
      
   2. 
      Цикл для j = 0 .. n – 1
      
      1. 
         Если !visited[j] и либо v == -1, либо d[j] < d[v]
         
         1. 
            Положим v = j
            
   3. 
      Положим visited[v] = true
      
   4. 
      Цикл для j = 0 .. n – 1
      
      1. 
         Если a[v][j] > 0 и d[v] + a[v][j] < d[j]
         
         1. 
            Положим d[j] = d[v] + a[v][j]
            
9. 
   Вывод d[last]
   

Результаты работы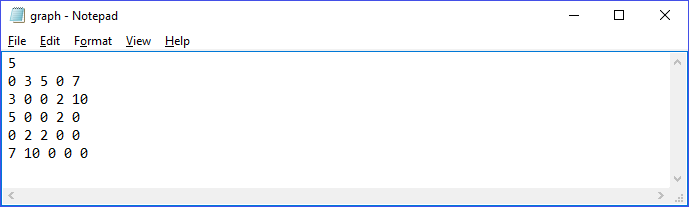

Рис. 1 Содержимое входного файла



Рис. 2 Кратчайший путь из вершины 1 в 4

Выводы

В результате выполнения этой лабораторной работы были получены навыки по реализации алгоритма Дейкстры для вычисления кратчайшего пути из одной вершины до другой.

Приложение А. Листинг программы

#include

#include

#include

#include
using namespace std;
const int INF = 1e5;
int n , m , st , last;

vector< vector > a;

vector visited;
int main() {

ifstream fin("graph.txt");

fin >> n; // Ввод количества вершин и количества ребер

a.assign(n , vector(n)); // Выделение памяти для матрицы весов

visited.assign(n , false); // Метим массив значениями false

for (int i = 0 ; i < n ; i++)

for (int j = 0 ; j < n ; j++)

fin >> a[i][j]; // Ввод матрицы весов

cout << "Input first vertex: "; cin >> st; // Ввод стартовой вершины

cout << "Input last vertex: "; cin >> last; // Ввод конечной вершины

st--;

last--;
vector d(n , INF); // Создаем массив расстояний

d[st] = 0; // От начальной вершины до нее самой расстояние = 0

for (int i = 0 ; i < n ; i++) { // Выполним n итераций

int v = -1; // v - вспомогательная вершина, через которую будем обновлять расстояния

for (int j = 0 ; j < n ; j++) // Цикл по всем вершинам

if (!visited[j] && (v == -1 || d[j] < d[v])) v = j; // Если эта вершина не посещена, и расстояние до этой вершины минимально, сохраним эту вершину

if (d[v] == INF) break; // Если через эту вершину уже обновиться не можем - выходим

visited[v] = true; // Метим, что вершина посещена

for (int j = 0 ; j < n ; j++) // Цикл по всем вершинам

if (a[v][j] > 0 && d[v] + a[v][j] < d[j]) // Если можем обновить

d[j] = d[v] + a[v][j]; // Обновляем массив расстояний

}

cout << "Minimal distance from first to last: ";

if (d[last] == INF) d[last] = -1;

cout << d[last];
return 0;

}