Аааа. Графтарда ашытытар. Граф диаметрі радиусы жне орталыы

• Название: Графтарда ашытытар. Граф диаметрі радиусы жне орталыы
• Дата: 23.12.2022
• Размер: 40.36 Kb.
• Имя файла: Ãðàôòàðäà ?àøû?òû?òàð. Ãðàô äèàìåòð³ ðàäèóñû æ?íå îðòàëû?û.docx
• Тип: Документы; #860495

Графтарда қашықтықтар. Граф диаметрі радиусы және орталығы
Айталық G = (V,X) – граф (жалпы жағдайда псевдограф) берілген болсын. Егер υ,ω V, υ ≠ ω төбелер болса, онда екі төбені жалғастыратын маршрут бар және олардың ішінен минимал маршрут табу мүмкіндігін байқаймыз. Шынында, егер к₁ ұзындықтағы q₁ маршрут минимал болмаса, онда к₂ < к₁ ұзындықтағы q₂ маршрут табылады. Егер q₂ маршрут минимал болмаса, онда к₃ < к₂ ұзындықтағы q₃ маршрут бар болады және т.б.

Осы секілді маршруттардың ұзындығын кемітуді (к₁–1) ретке дейін ғана мүмкіндігін көру қиын емес, себебі өте минимал маршруттың ұзындығы бірге тең. Соның үшін G да υ,ω төбелерді қосатын минимал маршрут міндетті түрде табылады.

Осы маршруттың ұзындығын d(υ,ω) арқылы белгілейміз. Сонымен кез келген υ V төбе үшін d(υ,υ)=0.Тағыда кез келген υ,ωV үшін G да υ,ω (υ≠ω)төбелерді қосатын маршрут болмаса, онда d(υ,ω) = +∞ немесе d(υ,ω) = ∞ ретінде жазамыз. Сонымен кез келген υ,ω V төбелер үшін d(υ,ω) шаманы анықтадық.

Осы d(υ,ω) – шаманы υ , ω төбелер арасындағы қашықтық деп айтамыз.

d(υ,ω) қашықтық метрикалық аксиомаларды қанағаттандырады:

1.d(υ,ω) ≥ 0, бұл жерде d(υ,ω) = 0 теңдік υ = ω болғанда және тек сонда ғана орынды ;

1. 
   d(υ,ω) = d(ω,υ);
   
2. 
   d(υ,ω) ≤ d(υ,u) + d(u,ω), бұл жерде υ,u,ω – G графтың кез келген төбесі ;
   
3. 
   d(υ,ω) < ∞.
   

Граф диаметрі, радиусы және орталығы.
Айталық G = (V,X) – байлаынсты граф немесе жалпы жағдайда псевдограф болсын.

1. Онда d(G) = max d(υ,ω)

υ,ω V

шекті шама болады және G графтың диаметрі деп айтылады.

2. Егер υ  V кез келген төбе болса, онда

r(υ) = max d(υ,ω)

ω V

шекті шама G графтағы υ төбенің максимал эксцентриситетті (алыстағы) нүктесі деп айтылады.

3. G графтың радиусы деп

r(G) = min r(υ)

υ V

шаманы айтамыз.

4. Кезкелген υ V үшін r(υ) = r(G) болған төбе G графтың орталығы деп айтылады.

19 – мысал. 16 – сызбада бейнеленген G граф үшін : d(G) = 3, r(υ₁) = 3, r(υ₂) = 2, r(υ₃) = 2, r(υ₄) = 2, r(υ₅) = 3, r(G) = 2 ; υ₂, υ₃, υ₄ – G графтың орталықтары.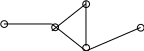

υ₃

υ₅

υ₁ υ₂

υ₄
16-сызба.
Графттарда минимал жане максимал бутақ ағаштары
Тиелген графтардың минимал бұтақ ағаштары.
Айталық байланысты G = (V,X) графтың әр бір xÎ X қабырғасына ℓ(x) – қабырқа ұзындығы сәйкес қойылған, яғни G тиелген граф болсын.

Анықтама. Байланысты тиелген G граф бұтақ ағашының өзінде болған қабырғалар ұзындықтары қосындысы минимал болған ағаш G графтың минимал бұтақ ағашы (МБА) деп айтылады.

Енді G граф үшін МБА табу алгоритімін келтіреміз.

Алгоритм № 7. (Байланысты тиелген G графтан МБА ны бөлү):

1 – қадам. G графта минимал ұзындықтағы қабырға айырып аламыз. Ол өзіне инцидентті болған төбемен G₂ ішграфты құрайды. i = 2 болсын.

2 – қадам. Егер i = n болса (n = n(G)), онда G₁ – ізделінген МБА деп қабылданып, мәселе соңына жетеді. Басқа жағдайда 3 – қадамға өтеміз.

3 – қадам. Енді G_i де жатпайтын, G_i графтағы қалайда бір төбеге инцидентті болған және G графтың барлық қабырғалары ішінен таңдалған минимал ұзындықтағы жаңа қабырғаны G_i графқа қосып G_i+1 граф құраймыз. Осы қабырғамен бірге оған инцидентті болған, бірақ G_i де жатпайтын төбеніде G_i+1 ге енгіземіз. i:=i+1 орындап 2 – қадамға өтеміз.

29 – мысал. 27 – сызбада бейнеленген G тиелген графтың МБА сын алгоритм негізінде анықтаймыз. 28 - сызбада алгоритмді орындау нәтижесінде алынған G_i, i = 2, 3,4,5 графтар тізбегі келтірілген. Бұл жерде n(G)=5 болғандықтан G графтың МБАсы G₅ болады.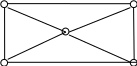

υ₂ 2 υ₃

1 u₅ 4

1 3

5 3

υ₁ 4 υ₄