Груз а груз В
 Скачать 150.35 Kb. Скачать 150.35 Kb.
|
|
Вариант 3 Решить задачу оптимального плана перевозок, если Т - установленная такса, А - матрица потребностей для перевозки трех видов грузов в тоннах, В - матрица возможностей заказчиков в млн. руб. Оценить результат расчетов. 3. 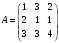 , , 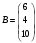 , Т=0,5. , Т=0,5. Составим таблицу потребностей и возможностей всех поставщиков:
Анализ таблицы показывает, что возможная прибыль до оптимизации цен будет равна 6+4+10 = 40 млн.р., а после нее 6+4+10 = 20 млн. р. То есть разница может составить 0 млн. р. Найдем оптимальное решение. Пусть 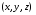 - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить 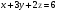 млн. р, второй млн. р, второй 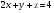 млн.р, третий млн.р, третий 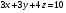 млн. р. млн. р. Получили систему из трех уравнений с тремя неизвестными:  Решим ее методом Крамера: 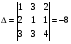 , ,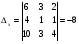 , ,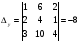 , ,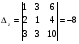 , ,откуда: 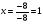 , , 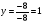 , , 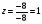 . .Ответ: Оптимальный план перевозок составляет 1, 1 и 1 (млн.р). за 1 т. веса продукции типа А, В и С соответственно. Получившаяся чистая прибыль составляет 1 (млн. р.) Вариант 3 3. Если 1) 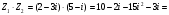 7-4i. 7-4i.4. Брошены два игральных кубика. Какова вероятность, что сумма выпавших очков будет равна 7? могут выпасть пары: 1-6 2-5 3-4 4-3 5-2 6-1 (итого 6 вариантов делим на общее кол-во 12) получается 6\12 =1\6 (ОТВЕТ=1\6) 5. Математическое ожидание, мода и дисперсия С,В, заданной таблично соответственно равны…
По определению математического ожидания: 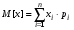 имеем: имеем: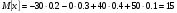 . .По определению дисперсии: 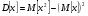 имеем: имеем: . .Модой дискретной случайной величины называется наиболее вероятное ее значение, при котором 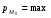 . Поэтому, в данном случае мода равна: . Поэтому, в данном случае мода равна: 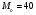 , т.к. ей соответствует максимальная вероятность равная 0,4. , т.к. ей соответствует максимальная вероятность равная 0,4.Вариант 4 4. А= 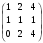 , В = , В = 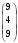 , Т=1 , Т=1Составим таблицу потребностей и возможностей всех поставщиков:
Анализ таблицы показывает, что возможная прибыль до оптимизации цен будет равна 7+3+6 = 16 млн.р., а после нее 9+4+9 = 22 млн. р. То есть разница может составить 6 млн. р. Найдем оптимальное решение. Пусть 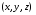 - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить 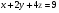 млн. р, второй млн. р, второй 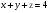 млн.р, третий млн.р, третий 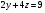 млн. р. млн. р. Получили систему из трех уравнений с тремя неизвестными: 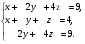 Решим ее методом Крамера: 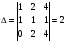 , ,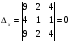 , ,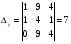 , ,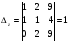 , ,откуда: 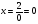 , , 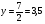 , , 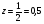 . .Ответ: Оптимальный план перевозок составляет 0;3,5 и 0.5 (млн.р). за 1 т. веса продукции типа А, В и С соответственно. Получившаяся чистая прибыль составляет 4 (млн. р.) 3 Если 1) 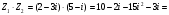 7-4i. 7-4i.4. Собрание, на котором присутствуют 20 человек, в том числе 8 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины. 20-8=12.человек мужчины 5/12=0.4 вероятность, что мужчины из 12 5/3=1.67 вероятность женщин из 3 1,67-0.4=1,27 т.е. 27%, что в делигацию войдут женщина из 3 человек 5. Математическое ожидание, мода и дисперсия С,В, заданной таблично соответственно равны…
По определению математического ожидания: 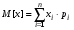 имеем: имеем: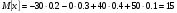 . .По определению дисперсии: 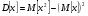 имеем: имеем: . .Модой дискретной случайной величины называется наиболее вероятное ее значение, при котором 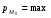 . Поэтому, в данном случае мода равна: . Поэтому, в данном случае мода равна: 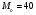 , т.к. ей соответствует максимальная вероятность равная 0,4. , т.к. ей соответствует максимальная вероятность равная 0,4.Вариант 5 5. 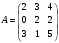 , , 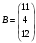 , Т=1 , Т=1 Составим таблицу потребностей и возможностей всех поставщиков:
Анализ таблицы показывает, что возможная прибыль до оптимизации цен будет равна 9+4+9 = 22 млн.р., а после нее 11+4+12 = 27 млн. р. То есть разница может составить 5 млн. р. Найдем оптимальное решение. Пусть 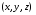 - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить 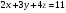 млн. р, второй млн. р, второй 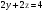 млн.р, третий млн.р, третий 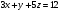 млн. р. млн. р. Получили систему из трех уравнений с тремя неизвестными: 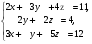 Решим ее методом Крамера: 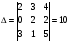 , ,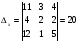 , ,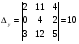 , ,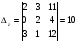 , ,откуда: 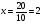 , , 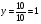 , , 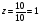 . .Ответ: Оптимальный план перевозок составляет 2, 1 и 1 (млн.р). за 1 т. веса продукции типа А, В и С соответственно. Получившаяся чистая прибыль составляет 2 (млн. р.) Вариант 5 3. Если 1) 5 2) 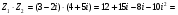 6-23i. 6-23i.4 Вероятность изготовления на станке-автомате нестандартной детали равна 0,02. Чему равна вероятность того, что среди наудачу взятых шести деталей окажется более четырех стандартных? Вероятность нестандартной детали q = 0,02 тогда вероятность стандартной: p = 1- 0,02 = 0,98 5. Математическое ожидание, мода и дисперсия С,В, заданной таблично соответственно равны
По определению математического ожидания: 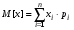 имеем: имеем: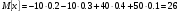 . .По определению дисперсии: 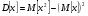 имеем: имеем: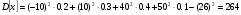 . .Модой дискретной случайной величины называется наиболее вероятное ее значение, при котором 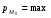 . Поэтому, в данном случае мода равна: . Поэтому, в данном случае мода равна: 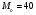 , т.к. ей соответствует максимальная вероятность равная 0,4. , т.к. ей соответствует максимальная вероятность равная 0,4.Вариант 10 10. 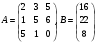 , Т=2 , Т=2 Составим таблицу потребностей и возможностей всех поставщиков:
Анализ таблицы показывает, что возможная прибыль до оптимизации цен будет равна 20+12+6 = 38 млн.р., а после нее 16+22+8 = 46 млн. р. То есть разница может составить 8 млн. р. Найдем оптимальное решение. Пусть 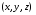 - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить - искомые цены на перевозки продукции типа А, В и С соответственно. Тогда первый поставщик должен заплатить 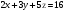 млн. р, второй млн. р, второй 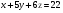 млн.р, третий млн.р, третий 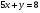 млн. р. млн. р. Получили систему из трех уравнений с тремя неизвестными: 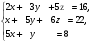 Решим ее методом Крамера: 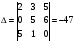 , ,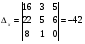 , ,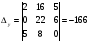 , ,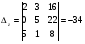 , ,откуда: 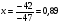 , , 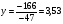 , , 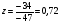 . .Ответ: Оптимальный план перевозок составляет 0.89; 3,53 и 0,72 (млн.р). за 1 т. веса продукции типа А, В и С соответственно. Получившаяся чистая прибыль составляет 3,53 (млн. р.) Вариант 10 3. Вычисление 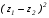 , если , если 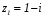 , , 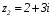 приводит к ответу… приводит к ответу…1) 289 2) -12 3) 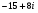 4) 4) 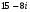  -12 -124. В первой урне 8 белых и 2 черных шара. Во второй урне 7 белых и 3 черных шара. В третьей урне 5 белых и 5 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар черный равна Р1=0,5*0,2=0,1; Р2=0,5*0,3=0,15; Р3 =0,5*0,5=1 Тогда искомая вероятность Р=Р1+Р2+Р3=0,1+0,2+1=1,25. 5 . Математическое ожидание, мода и дисперсия С,В, заданной таблично , соответственно равны…
По определению математического ожидания: 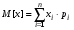 имеем: имеем: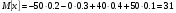 . .По определению дисперсии: 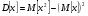 имеем: имеем: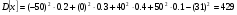 . .Модой дискретной случайной величины называется наиболее вероятное ее значение, при котором 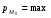 . Поэтому, в данном случае мода равна: . Поэтому, в данном случае мода равна: 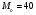 , т.к. ей соответствует максимальная вероятность равная 0,4. , т.к. ей соответствует максимальная вероятность равная 0,4. |
