гармоническая леаниризация. Характеристики нелинейного элемента
 Скачать 86.41 Kb.
|
|
Идея метода гармонической линеаризации принадлежит Н.М. Крылову и Н.Н. Боголюбову и базируется на замене нелинейного элемента системы линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Данный метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники.  Характеристики нелинейного элемента В случае нечувствительности нелинейной системы к высшим гармоникам нелинейный элемент может быть в первом приближении заменен некоторым элементом с эквивалентным коэффициентом передачи, который определяет первую гармонику периодических колебаний на выходе в зависимости от частоты и амплитуды синусоидальных колебаний на входе. Метод позволяет исследовать возможность появления автоколебательных режимов, определить основные параметры автоколебаний (A, ωа), качественно оценить влияние нелинейностей на устойчивость и переходные процессы в системе, как устранить автоколебания или же как изменить их параметры в желаемом направлении. Сущность метода гармонического баланса заключается в замене нелинейного элемента эквивалентным линейным, передаточный коэффициент которого не является постоянным, а зависит в общем случае от амплитуды и частоты искомых автоколебаний. Рассматривается замкнутая система с одним НЭ Изучается свободное движение системы, то есть движение при ненулевых начальных условиях в отсутствие внешних воздействий. В системе возможно возникновение автоколебаний. При этом z(t)- периодическая функция, содержащая спектр гармонических составляющих.      y(t) z(t) r(t)=0 ε(t)   Wл(p) F(ε)    + - Структурная схема системы с одним нелинейным элементом Метод гармонической линеаризации основан на nредnоложении, что колебания на входе нелинейного звена являются синусоидальны.ми,т. е. что  , (12.1)гдеА–амплитуда и  - частота этих автоколебаний , а  - возможная в общем случае постоянная составляющая, когда автоколебания несимметричны.В действительности автоколебания в нелинейных системах всегда несинусоидальны вследствие искажения их формы нелинейным звеном. Поэтому указанное исходное предположение означает, что метод гармонической линеаризации является принципиально приближенным и область его применения ограничена случаями, когда автоколебания на входе нелинейного звена достаточно близки к синусоидальным. Если при прохождении через линейную часть системы z(t) фильтруется так, что можно пренебречь всеми гармониками выше первой, то анализ системы можно вести методом гармонического баланса. Это предположение- необходимое условие применения метода гармонической линеаризации, его называют гипотезой фильтра, введено Е.П. Поповым. Поскольку высшие гармоники по амплитуде обычно меньше, чем первая гармоника, а линейная часть САУ узкополосная, устойчивая (могут быть нулевые корни характеристического уравнения линейной части), отсутствуют резонансные звенья, |W(jωa)| >>|W(jkωa)| при k >1, то во многих практических случаях гипотеза фильтра выполняется. Для приближённых расчётов последнее условие может быть смягчено и сформулировано так: наклон ЛАЧХ линейной части должен быть по крайней мере от -20 до -40 дБ/дек на частоте автоколебаний ωа и выполнены неравенства: при наклоне ЛАЧХ  ,  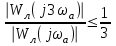,-20 дБ/декпри наклоне ЛАЧХ 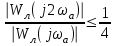 ,  .-40 дБ/декПри гармонической линеаризации нелинейные элементы заменяются их линейными моделями, полученными в результате изучения реакций на гармонические входные сигналы. На вход нелинейного элемента подаётся гармонический сигнал ε(t)=A·sinωt , выходная функция  z(t)=F(A·sinωt)- периодический (не гармонический) сигнал (рис. 5.36).Ограничимся рассмотрением безынерционных НЭ с петлевыми нечётносимметричными статическими характеристиками (простейшие НЭ). 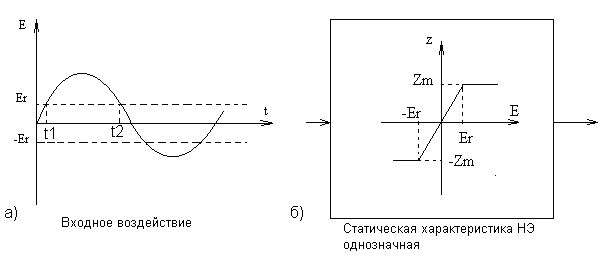 При исследовании нелинейных систем на основе метода гармонической линеаризации в первую очередь решают вопрос о существовании и устойчивости периодических режимов. Если периодический режим устойчив, то в системе существуют автоколебания 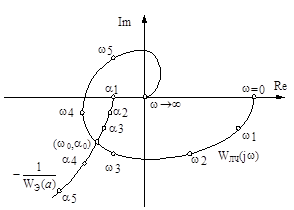 Годографы линейной и нелинейной частей системы На рис. дан пример расположения годографов для случая, когда в нелинейной системе существуют устойчивые автоколебания. Параметры автоколебаний на входе нелинейного элемента определяются в точке пересечения годографов:  Логарифмические амплитудные и фазовая характеристики 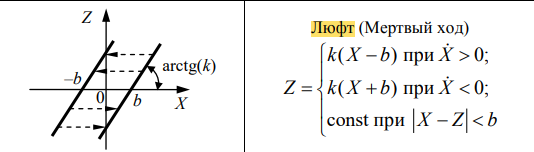 Статистическая характеристика и уравнения типовых нелинейностей |