Курсовая Хэширование с цепочками. курсовая1. Хеширование с цепочками
 Скачать 261 Kb. Скачать 261 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Институт математики, естественных наук И информационных технологий Кафедра программного обеспечения КУРСОВАЯ РАБОТА По предмету Структуры и алгоритмы компьютерной обработки данных На тему: Хеширование с цепочками. Выполнила: Студентка 304-1 группы Киселева Елена Александровна Проверила: ст.преподаватель кафедры программного обеспечения Киприна Елена Александровна Т  юмень-2012 юмень-2012 Аннотация В теоретической части курсовой работы предоставлен материал исследования на тему: «Хеширование с цепочками». С хешированием мы сталкиваемся едва ли не на каждом шагу: при работе с браузером (список Web-ссылок), текстовым редактором и переводчиком (словарь), языками скриптов (Perl, Python, PHP и др.), компилятором (таблица символов). По словам Брайана Кернигана, это «одно из величайших изобретений информатики». Заглядывая в адресную книгу, энциклопедию, алфавитный указатель, мы даже не задумываемся, что упорядочение по алфавиту является не чем иным, как хешированием. Практичееская часть представляет собой демонстрационную программу, включающая хеш-таблицу, поле для ввода ключа, счетчик коллизий, необходимые управляющие элементы и пояснения. Программа реализует процедуру записи ключа в таблицу и процедуру его поиска.  Содержание Теоретическая часть. 1.1 Введение…………………………………………………………………………………….4 1.2 Хеш-функции………………………………………………………………………………...6 1.2.1 Метод деления……………………………………………………………………………..6 1.2.2 Метод умножения………………………………………………………………………….7 1.3 Разрешение коллизий. Хеширование с цепочками………………………………………..9 1.3.1 Реализация основных процедур и функций для работы с хеш-таблицами (Паскаль)...9 1.3.2 Оценка времени работы операций для хеширования с цепочками…………………...13 Практическая часть. Демонстрационная программа. 2.1 Описание……………………………………………………………………………………14 2.2Техническое описание программы………………………………………………………..14 2.3 Скриншот демонстрационной программы………………………………………………..14 2.4 Обработчики событий……………………………………………………………………..15 2.5 Основные процедуры и функции…………………………………………………………15 Заключение…………………………………………………………………………………………………19 Список литературы……………………………………………………………………………………..20 Теоретическая часть 1.1 Введение Хеширование полезно там, где необходимо большой диапазон возможных значений сохранить в небольшом объеме памяти, и отыскать простым, почти произвольным доступом. Также, хэш-таблицы часто используются в базах данных и, особенно в языковых процессорах типа компиляторов и ассемблеров, где они обслуживают таблицы идентификаторов. В таких приложениях, хэш-таблица - принципиальная структура данных. Так как всякий доступ к таблице должен быть выполнен через хэш-функцию, то она должна удовлетворять двум требованиям: она должна работать быстро, и выдавать хорошие ключи распределения по таблице. С хешированием мы сталкиваемся едва ли не на каждом шагу: при работе с браузером (список Web-ссылок), текстовым редактором и переводчиком (словарь), языками скриптов (Perl, Python, PHP и др.), компилятором (таблица символов). По словам Брайана Кернигана, это «одно из величайших изобретений информатики». Заглядывая в адресную книгу, энциклопедию, алфавитный указатель, мы даже не задумываемся, что упорядочение по алфавиту является не чем иным, как хешированием. Хеширование есть разбиение множества ключей (однозначно характеризующих элементы хранения и представленных, как правило, в виде текстовых строк или чисел) на непересекающиеся подмножества (наборы элементов), обладающие определенным свойством. Это свойство описывается функцией хеширования, или хеш-функцией, и называется хеш-адресом. Решение обратной задачи возложено на хеш-структуры (хеш-таблицы): по хеш-адресу они обеспечивают быстрый доступ к нужному элементу. В идеале для задач поиска хеш-адрес должен быть уникальным, чтобы за одно обращение получить доступ к элементу, характеризуемому заданным ключом (идеальная хеш-функция). Однако, на практике идеал приходится заменять компромиссом и исходить из того, что получающиеся наборы с одинаковым хеш-адресом содержат более одного элемента. Термин «хеширование» (hashing) в печатных работах по программированию появился сравнительно недавно (1967 г., [1]), хотя сам механизм был известен и ранее. Глагол «hash» в английском языке означает «рубить, крошить». Для русского языка академиком А.П. Ершовым [2] был предложен достаточно удачный эквивалент — «расстановка», созвучный с родственными понятиями комбинаторики, такими как «подстановка» и «перестановка». Однако он не прижился. Как отмечает Дональд Кнут [3], идея хеширования впервые была высказана Г.П. Ланом при создании внутреннего меморандума IBM в январе 1953 г. с предложением использовать для разрешения коллизий хеш-адресов метод цепочек. Примерно в это же время другой сотрудник IBM – Жини Амдал – высказала идею использования открытую линейную адресацию. В открытой печати хеширование впервые было описано Арнольдом Думи (1956), указавшим, что в качестве хеш-адреса удобно использовать остаток от деления на простое число. А. Думи описывал метод цепочек для разрешения коллизий, но не говорил об открытой адресации. Подход к хешированию, отличный от метода цепочек, был предложен А.П. Ершовым (1957, [2]), который разработал и описал метод линейной открытой адресации. Среди других исследований можно отметить работу Петерсона (1957, [4]). В ней реализовывался класс методов с открытой адресацией при работе с большими файлами. Петерсон определил открытую адресацию в общем случае, проанализировал характеристики равномерного хеширования, глубоко изучил статистику использования линейной адресации на различных задачах. В 1963 г. Вернер Букхольц [6] опубликовал наиболее основательное исследование хеш-функций. К концу шестидесятых годов прошлого века линейная адресация была единственным типом схемы открытой адресации, описанной в литературе, хотя несколькими исследователями независимо была разработана другая схема, основанная на неоднократном случайном применении независимых хеш-функции ([3], стр. 585). В течение нескольких последующих лет хеширование стало широко использоваться, хотя не было опубликовано никаких новых работ. Затем Роберт Моррис [5] обширный обзор по хешированию и ввел термин «рассеянная память» (scatter storage). Эта работа привела к созданию открытой адресации с двойным хешированием. Далее будут рассмотрены основные виды хеш-функций и некоторые их модификации, метод разрешения коллизий с помощью цепочек. 1.2 Хеш-функции Хеш-функция – это некоторая функция h(K), которая берет некий ключ K и возвращает адрес, по которому производится поиск в хеш-таблице, чтобы получить информацию, связанную с K. Например, K – это номер телефона абонента, а искомая информация – его имя. Функция в данном случае нам точно скажет, по какому адресу найти искомое. Выбранная хеш-функция должна удовлетворять двум требованиям: предусматривать быстрое вычисление и минимизировать количество коллизий. Хеш-функция, не порождающая коллизий, называется совершенной. Нет смысла искать совершенную хеш-функцию, если множество ключей не является постоянным, но даже для конкретного набора ключей найти совершенную хеш-функцию очень сложно. На практике для выбора хеш-функций применяются эвристические подходы, учитывающие специфику задачи и ключа. Как правило, ключи целого типа или числового с плавающей точкой можно преобразовать за одну машинную операцию, в то время как строковые или составные ключи требуют больших затрат. 1.2.1 Метод деления. Метод деления весьма прост – используется остаток от деления на M: h(K) = K mod M Надо тщательно выбирать эту константу. Если взять ее равной 100, а ключом будет случить год рождения, то распределение будет очень неравномерным для ряда задач (идентификация игроков юношеской бейсбольной лиги, например). Более того, при четной константе значение функции будет четным при четном K и нечетным - при нечетном, что приведет к нежелательному результату. Еще хуже обстоят дела, если M – это степень счисления компьютера, поскольку при этом результат будет зависеть только от нескольких цифр ключа справа. Точно также можно показать, что M не должно быть кратно трем, поскольку при буквенных ключах два из них, отличающиеся только перестановкой букв, могут давать числовые значения с разностью, кратной трем (см. [3], стр. 552). Приведенные рассуждения приводят к мысли, что лучше использовать простое число. В большинстве случаев подобный выбор вполне удовлетворителен. 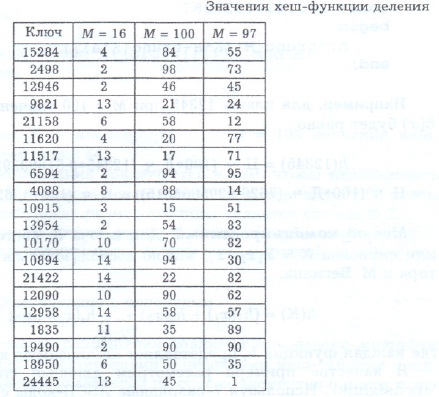 Таб1. Значение хеш-функции деления В таблице 1 представлены результаты вычисления h(x) для целых 16-разрядных случайных ключей при M=16, 100 и 97. Легко заметить случаи коллизии: например, для М=16 пять различных ключей имеют хеш-адрес, равный 2, для М=100 два ключа имеют хеш-адрес, равный 90, для М=97 два ключа имеют хеш-адрес, равный 82. На практике, метод деления – самый распространенный. 1.2.2 Метод умножения. Пусть ключ является w-битовым целым числом. Положим, h(К)=Ц.ч.(М*Д.ч.(К*q)), где q- константа от 0 до 1, Ц.ч. –целая часть чила, Д.ч. – дробная часть числа. Достоинство метода умножения в том, что значаения хеш-функции мало зависят от выбора М. Обычно в качестве М используют степень двойки – 2^n, тогда умножение на М реализуется как сдвиг на n битов влево. Последовательность вычисления хеш-функции следующая: Ключ К, представленный в виде w-битового числа, умножается на w-битовое число q2^w. Получается 2w-битовое число, у которого берут младшие wбит. Из выделенных битов выделяют nстарших. Таким образом, хеш-функция состоит из nстарших битов правой половины произведения Кq2^w. Выбор qне принципиален. 1.3 Разрешение коллизий. Хеширование с цепочками. Несмотря на то, что два или более ключей могут хешироваться одинаково, они не могут занимать в хеш-таблице одну и ту же ячейку. Нам остаются два пути: либо найти для нового ключа другую позицию в таблице, либо создать для каждого значения хеш-функции отдельный список, в котором будут все ключи, отображающиеся при хешировании в это значение. Оба варианта представляют собой две классические стратегии разрешения коллизий – открытую адресацию с линейным перебором и метод цепочек. В данной курсовой работе я рассмотрела разрешение коллизий при помощи метода цепочек. В данном походе к хешированию таблица рассматривается как массив связанных списков или деревьев. Каждый такой список называется блоком (bucket) и содержит записи, отображаемые хеш-функцией в один и тот же табличный адрес. Эта стратегия разрешения коллизий называется методом цепочек (chaining with separate lists). Если таблица является массивом связанных списков, то элемент данных просто вставляется в соответствующий список в качестве нового узла. Элементы такого списка могут находиться как в самой таблице, так и в отдельной памяти. В первом случае цепочки называются внутренними, во втором – внешними. Чтобы обнаружить элемент данных, нужно применить хеш-функцию для определения нужного связанного списка и выполнить там последовательный поиск. 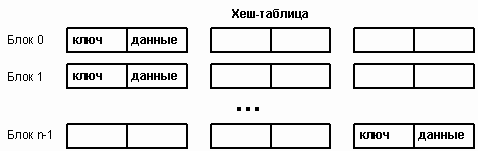 1.3.1 Реализация основных процедур и функций для работы с хеш-таблицами (Паскаль). 1) Структура данных для хеш-таблицы с внешними цепочками может быть описана следующим образом: Type Chain=^Item; Item=record Key:Tkey; Info: Tinfo; Next: chain End; CHTable=array[0..M-1] of Chain; 2) Операция инициализации хеш-таблицы присваивает всем указателям на списки, хранящимся в таблице, значение nil; Procedure TableInit (var T:CHTable); Var i:integer; Begin For i:=0 to M-1 do T[i]:=nil; End; 3) Операция поиска xв хеш-таблице Т реализована как последовательный поиск в списке с адресом T[h(x)]. Функция CHSearch возвращает указатель на элемент, содержащий ключ х, или nil, в случае неудачного поиска: Function CHSearch(x: Tkey; var T:CHTable): chain; Var P: chain; Begin P:=T[h(x)]; While (P< >nil) and (P^.key< >x) do P:=P^.next; CHSearch:=P; End; 4) Операция вставки ключа х основана на неудачном поиске в списке, начинающемся с адреса T[h(x)]? После чего реализуется вставка в начало списка: Procedure CHInsert(x: Tkey; var T: CHTable); Var P: chain; i:integer; Begin I:=h(x); P:=T[i]; While (P< >nil) and (P^.key< >x) do P:=P^.next; If P=nil then Begin P:=T[i]; New(T[i]); T[i]^.key:=x; T[i]^.next:=P; End; End; 5) При удалении элемента xопределённое неудобство доставляет односвязность списка, поэтому при поиске х следует использовать второй указатель – на предшествующий элемент (заметим, что этого можно было бы избежать, если пожертвовать памятью и хранить цепочки в виде двухсвязных списков). Особо рассматривается случай, когда xнаходится в первой ячейке списка: Procedure CHDelete (x: Tkey; var T: CHTable); Var P,Q: chain; i: integer; Begin I:=h(x); If T[i]<>nil then Begin If T[i]^.key=x then Begin Q:=T[i]; T[i]:=T[i]^.next; Dispose(Q) end Else Begin P:=T[i]; Q:=P^.next; While (Q<>nil) and (Q^.key<>x) do Begin P:=Q; Q:=Q^.next end; If Q<>nil then Begin P^.next:=Q^.next; Dispose(Q) end End; End; End; 1.3.2 Оценка времени работы операций для хеширования с цепочками. В худшем случае на поиск будет тратится время O(N) , когда все хеш-адреса одинаковы, все элементы таблицы попадают в один список длины Nи операция поиска сводится к последовательному поиску в списке. Среднее время поиска зависит от того, насколько равномерно хеш-функция распределяет хеш-адреса. Предположим, что хеширование равномерно, то есть каждый из элементов может попасть в любую из М позиций таблицы с равной вероятностью. Определим величину q=N/M, равную средней длине цепочек, тогда время выполнения операций оценивается в терминах коэффициента q. Справедливо следующее утверждение: Среднее время неуспешного поиска равно О(1+q); Cреднее время удачного поиска равно О(1+q/2); 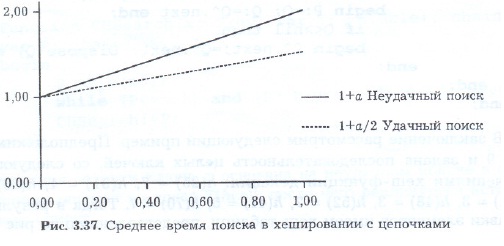 Рис. 2 Практическая часть. Демонстрационная программа. 2.1 Описание. Практичееская часть представляет собой демонстрационную программу, включающая хеш-таблицу, поле для ввода ключа, счетчик коллизий, необходимые управляющие элементы и пояснения. Программа реализует процедуру записи ключа в таблицу и процедуру его поиска. 2.2Техническое описание программы. Среда программирования-Delphi; Требуемая операционная система: Windows xp,7,Vista; Используемая дисковая память: 460 КБ Требования к компьютеру: процессор(Intel Pentium 233 МГц и выше), оперативная память(64 Мбайт (рекомендуется 128 Мбайт)), монитор(SVGA или выше). 2.3 Скриншот демонстрационной программы. 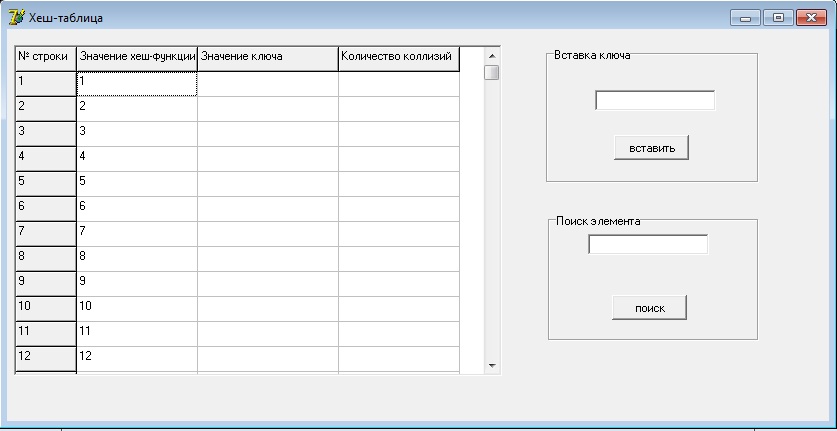   Кнопка вставки ключа (btn1)  Хеш-таблица (компонент strngrd1) Кнопка поиска элемента(btn 2) Обработчики событий. Реализация добавления ключа. Обработчик события OnClick события btn1. procedure TForm1.btn1Click(Sender: TObject); var ch:integer; begin ch:=strtoint(Edt1.Text); AddElem(ch,20); end; Поиск элемента. Обработчик события OnClick события btn2. procedure TForm1.btn2Click(Sender: TObject); begin FindElem(strtoint(Edt2.Text),20); end; Основные процедуры и функции. Добавление элемента по ключу. procedure AddElem(key:integer;c:integer); var position:integer; p,cur:pElem; begin position:=HF(key,c); GetMem(p,sizeof(Elem)); p^.key := key; p^.next:=nil; cur:=HT[position]; if cur=nil then HT[position]:=p else begin while cur^.next<>nil do begin cur := cur^.next; end; cur^.next := p; end; if(Form1.strngrd1.Cells[2,position]<>'') then Form1.strngrd1.Cells[2,position]:=Form1.strngrd1.Cells[2,position]+'->'+inttostr(key) else Form1.strngrd1.Cells[2,position]:=Form1.strngrd1.Cells[2,position]+inttostr(key); if Form1.strngrd1.Cells[3,position]='' then Form1.strngrd1.Cells[3,position]:='0' else Form1.strngrd1.Cells[3,position]:=inttostr(strtoint(Form1.strngrd1.Cells[3,position])+1); end; Поиск элемента по ключу. procedure FindElem(key:integer;c:integer); var position:integer; cur:pElem; find:boolean; begin find:=false; position:=HF(key,c); cur := HT[position]; while (not find) and (cur<>nil) do begin if cur^.key = key then find:=true; cur:=cur^.next; end; if not find then Form1.Lbl1.Caption:='Ничего не найдено' else Form1.lbl1.Caption:= 'Найдено в строке '+ inttostr(position); end; Вычисление хеш-функции. function HF(t:integer;cm:integer):integer; //хеш функция var A,B,C:Mnog; begin InitMnog(A); InitMnog(B); InitMnog(C); From2(t,A); From2(cm,B); DivMnog(A,B,C); HF := trunc(To2(C)); end; Заключение Основным недостатком хеширования по сравнению другими методами, основанными на динамическом размещении, - это фиксированный размер таблиц и невозможность настройки на реальные требования, поэтому нужно научиться достаточно хорошо заранее оценивать число классифицируемых элементов. Другой недостаток методов, основанных на хешировании, становится сразу же очевидным, как только заходит речь о том, что ключи нужно не только вставлять в таблицу и отыскивать, но и исключать из таблицы. Изъятие строки из хеш-таблицы – вещь крайне трудная, если только не используются явные списки в отдельной области переполнения. Однако, хеширование, которое родилось еще в середине прошлого века, активно используется в наши дни везде, где требуется произвести быструю выборку данных. Список литературы Hellerman H., Digital Computer System Principles. McGraw-Hill, 1967. Ершов А.П., Избранные труды., Новосибирск: «Наука», 1994. Кнут Д., Искусство программирования, т.3. М.: Вильямс, 2000. Peterson W.W., Addressing for Random-Access Storage // IBM Journal of Research and Development, 1957. V.1, N2. Р.130—146. Morris R., Scatter Storage Techniques // Communications of the ACM, 1968. V.11, N1. Р.38—44. Buchholz W., IBM Systems J., 2 (1963), 86–111 Вирт Н., Алгоритмы и структуры данных, СПб.: Невский диалект, 2008. А.Ю. Деревнина. Структуры и алгоритмы компьютерной обработки данных: учебное пособие. Тюмень: Издательство Тюменского государственного университета, 2005. http://bitsofmind.wordpress.com/2008/07/28/introduction_in_hash_tables/ http://www.rsdn.ru/article/alg/bintree/hash.xml |
