Химический факультет кафедра физической химии
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского» (ННГУ) ХИМИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА ФИЗИЧЕСКОЙ ХИМИИ ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ «ОПРЕДЕЛЕНИЕ ЁМКОСТИ КОНДЕНСАТОРА» Преподаватель: доцент Машин Н.И. Исполнители: студенты 1 курса в/о группы 0221Б2ХМ Гладкова А. Чучина Е. Балакина А. Рябинина А. г. Нижний Новгород 2022 г ОглавлениеВведение 1 Теоретическая часть 1 Практическая часть 4 ВведениеЦель работы: определить емкость конденсатора при помощи мостиковой схемы. В соответствии с целью работы составлены следующие задачи: изучить теоретический материал по данной теме; определить погрешности измерений. В ходе работы для достижения поставленных целей и задач были использованы теоретические методы, такие как изучение специальной литературы, в практической части работы использовались методы эксперимент, измерение, наблюдение. Теоретическая частьЭлектроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками. Конденсатор – устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Тогда можно записать формулу электроемкости конденсатора: 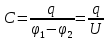 . (1) . (1)Значением φ1 − φ2 = U обозначают разность потенциалов, называемую напряжением U [1]. Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит от заряда проводника и его потенциала. Единица измерения электроемкости – фарад (Ф). 1 Ф – ёмкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл. Конденсатор состоит на двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делят на плоские, цилиндрические и сферические (рис. 1) [2]. 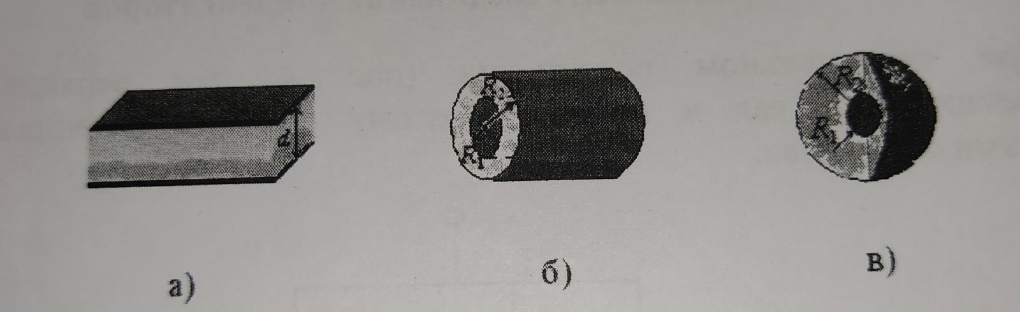 Рис. 1. Конденсаторы: а – плоский; б – цилиндрический; в - сферический. Емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии dдруг от друга и имеющие заряды +Q и –Qопределяется: 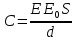 , (2) , (2)где 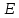 - относительная диэлектрическая проницаемость диэлектрика конденсатора, - относительная диэлектрическая проницаемость диэлектрика конденсатора, 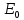 = 8.85·10-12 Ф/м – диэлектрическая постоянная. = 8.85·10-12 Ф/м – диэлектрическая постоянная.Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусами R1,R2 и длины L. Емкость цилиндрического конденсатора определяется: 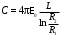 . (3) . (3)Сферический конденсатор представляет собой систему, состоящую из концентрических проводящих сфер радиусами R1иR2. Емкость сферического конденсатора рассчитывается: 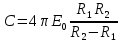 . (4) . (4)Для увеличения емкости и варьирования ее возможных значений конденсаторы в батареи, при этом используются их параллельные и последовательные соединения. При параллельном соединении (рис. 2) все верхние обкладки эквипотенциальны, как и нижние, поэтому разность потенциалов между обкладками одинакова. 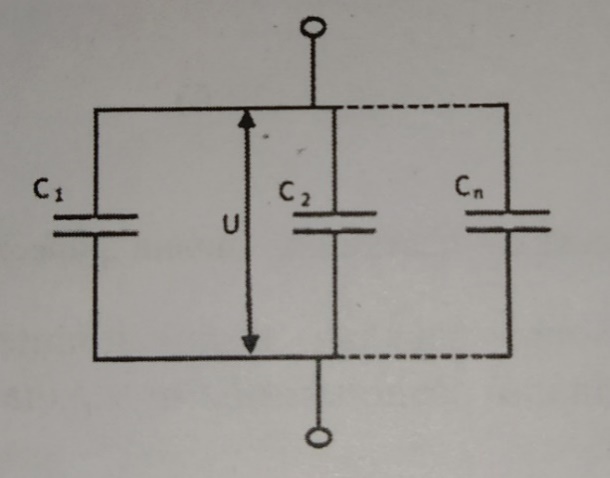 Рис. 2. Параллельное соединение конденсаторов U1 = U2 = . . . = Un. (5) Заряд на всех верхних обкладках равен сумме зарядов на каждой верхней обкладке: Q = Q1 + Q2 + . . . + Qn = 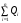 . (6) . (6)Согласно (1) формула (6) перепишется в виде: 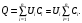 (7) (7)Емкость всей батареи конденсаторов по определению равна: 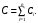 (8) (8)То есть при параллельном соединении емкости конденсаторов складываются. При последовательном соединении (рис. 3) полное напряжение на всей батарее конденсаторов равно сумме напряжений на каждом конденсаторе, а заряды одинаковы: 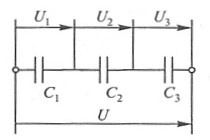 Рис. 3. Последовательное соединение конденсаторов. U = U1 + U2 + . . . + Un = 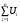 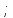 (9) (9)Q1 = Q2 = . . . = Qn ; (10) 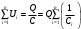 ; (11) ; (11)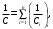 (12) (12)то есть при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость всегда меньше наименьшей емкости, используемая в батарее. Практическая частьПриборы: конденсаторы, гальванометр, аккумуляторная батарея, переключатель. Для измерения емкости конденсатора широко используются мостиковые схемы. Примером может служить мостиковая схема, изображенная на рис. 4. 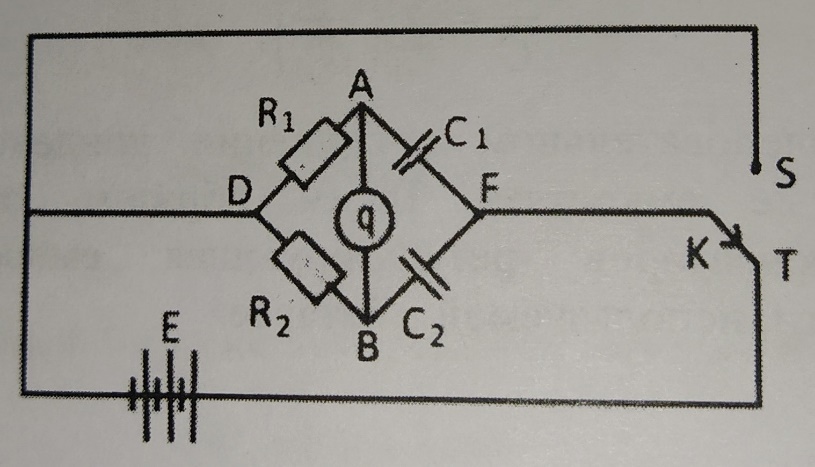 Рис. 4. Схематическое изображение мостиковой схемы. Схема состоит из двух конденсаторов C1 и C2, гальванометра g, аккумуляторной батареи E и переключателя K. Для такой схемы справедливо равенство: C1R1 = C2R2. (13) Зная C1 и подбирая R1 и R2, сможем вычислить C2 для трёх разных конденсаторов. Каждый опыт был выполнен 3 раза, полученные данные были занесены в таблицу 1. Величину C2 вычислили по формуле: 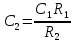 . (14) . (14)Расчет погрешности По формуле (14) рассчитали погрешность приборов: Прологарифмируем 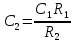 : :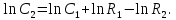 (15) (15) Таблица 1. Результат работы по определению емкости конденсатора.
Дифференцируем (15): 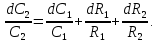 (16) (16)Погрешность приборов: ΔR1 = 0.02 Ом; ΔR2 = 0.02 Ом и ΔC1 = 0.01 мкФ. Uβ = 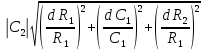 = =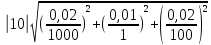 =10 =10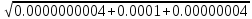 = =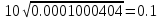 мкФ. мкФ.Погрешность измерений равна: 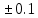 мкФ. мкФ.Вывод. С помощью мостиковой схемы определили емкости трех конденсаторов: 10.0 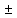 0.1 мкФ, 6.0 0.1 мкФ, 6.0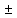 0.1 мкФ, 15.3 0.1 мкФ, 15.3 0.1 мкФ. 0.1 мкФ.Литература https://zaochnik.com/spravochnik/fizika/elektricheskoe-pole/emkost-kondensatorov/ - Эл. портал ZAOCHNIK.COM - Ёмкость конденсатора: определение, формулы, примеры. Трофимова Т. И.: учеб. Пособие для вузов/ Т.И. Трофимова. – 15-е изд., стер. – М.: Издательский центр «Академия», 2007. – 560 с. – C. 170 – 173. Приложение 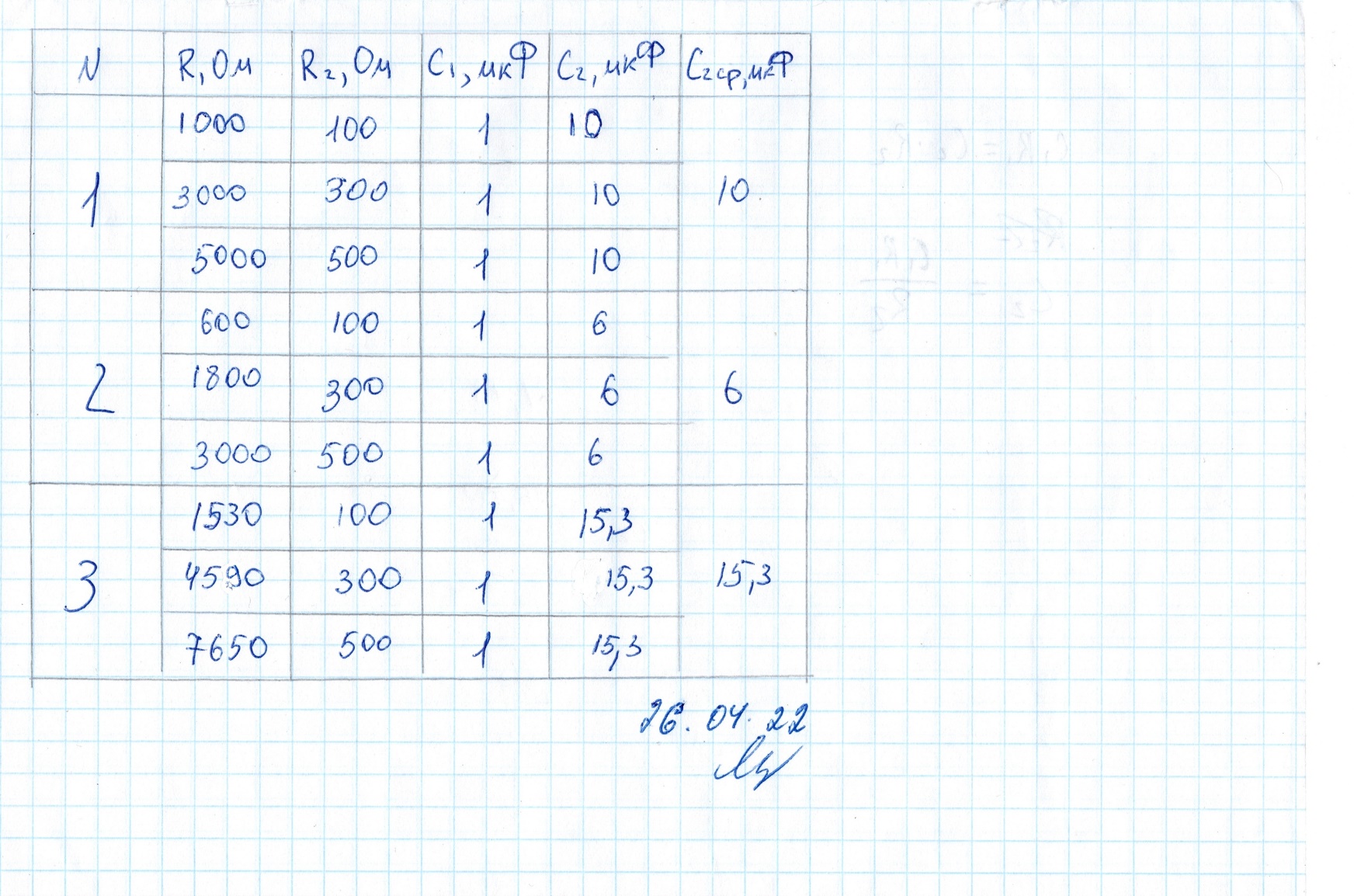 |
