Резюме. Httpsyandex ruvideopreviewtext%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8%D0%B8%D0%B7%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2&pathwizard&parentreqid163152515121917114493664122447709494sas3103050bsasl7balancer8080bal8583&wiz
 Скачать 26.2 Kb. Скачать 26.2 Kb.
|
|
https://yandex.ru/video/preview/?text=%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8+%D0%B8%D0%B7+%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8+%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2&path=wizard&parent-reqid=1631525151219171-14493664122447709494-sas3-1030-50b-sas-l7-balancer-8080-BAL-8583&wiz_type=vital&filmId=7347797903727887965&url=http%3A%2F%2Ffrontend.vh.yandex.ru%2Fplayer%2F6467491080446059324 https://yandex.ru/video/preview/?text=%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8+%D0%B8%D0%B7+%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8+%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2&path=wizard&parent-reqid=1631525151219171-14493664122447709494-sas3-1030-50b-sas-l7-balancer-8080-BAL-8583&wiz_type=vital&filmId=4915209849934188115&url=http%3A%2F%2Ffrontend.vh.yandex.ru%2Fplayer%2FvfWH-ald7-Rg Задача о выборе оборудования. На приобретение оборудования для нового участка цеха выделено 20000 долларов США. При этом можно занять площадь не более 38 м2. Имеется возможность приобрести станки типа А и станки типа Б. При этом станки типа А стоят 5000 долларов США, занимают площадь 8 м2 (включая необходимые технологические проходы) и имеют производительность 7 тыс. единиц продукции за смену. Станки типа Б стоят 2000 долларов США, занимают площадь 4 м2 и имеют производительность 3 тыс. единиц продукции за смену. Необходимо рассчитать оптимальный вариант приобретения оборудования, обеспечивающий при заданных ограничениях максимум общей производительности участка. Задача о ранце. Общий вес ранца заранее ограничен. Какие предметы положить в ранец, чтобы общая полезность отобранных предметов была максимальна? Вес каждого предмета известен. Есть много эквивалентных формулировок. Например, можно вместо ранца рассматривать космический аппарат – спутник Земли, а в качестве предметов - научные приборы. Тогда задача интерпретируется как отбор приборов для запуска на орбиту. Правда, при этом предполагается решенной предварительная задача - оценка сравнительной ценности исследований, для которых нужны те или иные приборы. С точки зрения экономики предприятия и организации производства более актуальна другая интерпретация задачи о ранце, в которой в качестве «предметов» рассматриваются заказы (или варианты выпуска партий тех или иных товаров), в качестве полезности – прибыль от выполнения того или иного заказа, а в качестве веса – себестоимость заказа. Перейдем к математической постановке. Предполагается, что имеется n предметов, и для каждого из них необходимо решить, класть его в ранец или не класть. Для описания решения вводятся булевы переменные Хk , k = 1,2,…, n (т.е. переменные, принимающие два значения, а именно, 0 и 1). При этом Хk = 1, если предмет размещают в ранце, и Хk = 0, если нет, k = 1,2,…, n. Для каждого предмета известны две константы: Аk - вес k-го предмета, и Сk - полезность k-го предмета, k = 1,2,…, n . Максимально возможную вместимость ранца обозначим В. Оптимизационная задача имеет вид C1 Х1 + С2 Х2 + С3 Х3 + …. + СnХn → max , А1 Х1 + А2 Х2 + А3 Х3 + …. + АnХn ≤ В. В отличие от предыдущих задач, управляющие параметры Хk , k = 1,2,…, n , принимают значения из множества, содержащего два элемента - 0 и 1. К целочисленному программированию относятся задачи размещения (производственных объектов), теории расписаний, календарного и оперативного планирования, назначения персонала и т.д. (см., например, монографию [2]). Укажем два распространенных метода решения задач целочисленного программирования Метод приближения непрерывными задачами. В соответствии с ним сначала решается задача линейного программирования без учета целочисленности, а затем в окрестности оптимального решения ищутся целочисленные точки. Методы направленного перебора. Из них наиболее известен метод ветвей и границ. Суть метода такова. Каждому подмножеству Х множества возможных решений Х0 ставится в соответствие число - "граница" А(Х). При решении задачи минимизации необходимо, чтобы А(Х1) ≥ А(Х2), если Х1 входит в Х2 или совпадает с Х2 . Каждый шаг метода ветвей и границ состоит в делении выбранного на предыдущем шаге множества ХС на два - Х1С и Х2С. При этом пересечение Х1С и Х2С пусто, а их объединение совпадает с ХС . Затем вычисляют границы А(Х1С ) и А(Х2С) и выделяют "ветвь" ХС+1 - то из множеств Х1С и Х2С, для которого граница меньше. Алгоритм прекращает работу, когда диаметр вновь выделенной ветви оказывается меньше заранее заданного малого числа Алгоритм решения задачи о рюкзаке ( версия 2, исправленная) https://habr.com/ru/post/222577/ Задача о кратчайшем пути. Как кратчайшим путем попасть из одной вершины графа в другую? В терминах производственного менеджмента: как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример (рис.7). 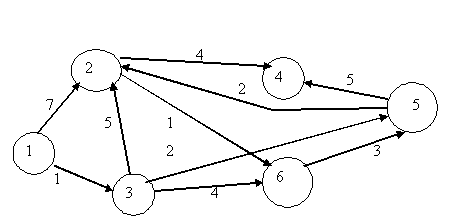 Рис.7. Исходные данные к задаче о кратчайшем пути. Ситуацию можно описать не только ориентированным графом с весами, приписанными дугам, но и таблицей (табл.7). В этой таблице двум вершинам – началу пути и концу пути – ставится в соответствие время в пути. В табл.7 рассматриваются пути без промежуточных остановок. Более сложные маршруты составляются из элементарных отрезков, перечисленных в табл.4. Таблица 4. Исходные данные к задаче о кратчайшем пути.
Спрашивается в задаче: как кратчайшим путем попасть из вершины 1 в вершину 4? Задача о максимальном потоке. Как (т.е. по каким маршрутам) послать максимально возможное количество грузов из начального пункта в конечный пункт, если пропускная способность путей между пунктами ограничена? Для решения этой задачи каждой дуге ориентированного графа, соответствующего транспортной системе, должно быть сопоставлено число - пропускная способность этой дуги. Рассмотрим пример 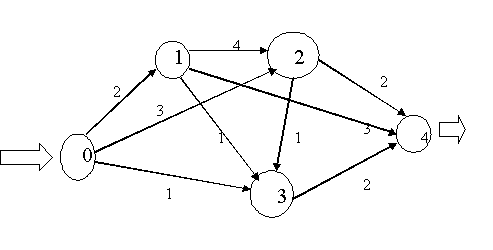 Решение задачи о максимальном потоке может быть получено из следующих соображений. Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3. Таблица 5. Исходные данные к задаче о максимальном потоке
Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу - в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4). В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 2. Их направляем в пункт 4. Итак, максимальная пропускная способность рассматриваемой транспортной системы - 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 - по ней направлены 2 единицы груза при пропускной способности в 3 единицы. Решение можно представить в виде таблицы |
