Подготовка к КР по математике. I. Классификация Уравнений Математической Физики (умф). 1) Порядок
 Скачать 16.52 Kb. Скачать 16.52 Kb.
|
|
I. Классификация Уравнений Математической Физики (УМФ). 1) Порядок: Порядок смотрится по старшей производной и обозначается буквой n: Примеры: 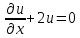 n=1; n=1;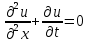 n=2. n=2.2) Линейность: Как я понял, что-то тип линейности функции, мб на этом принципе завязано Примеры: 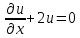 – линейное; – линейное; 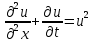 – нелинейное; – нелинейное;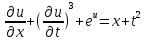 – нелинейное. – нелинейное.Степень х и t на линейность не влияют: 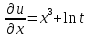 – линейное; – линейное;3) Однородность: Есть производные, но нет переменных – однородное, есть производные и переменные – неоднородное. Примеры: 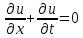 – однородное; – однородное;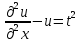 – неоднородное. – неоднородное.4) С постоянными или с переменными коэффициентами: Примеры: 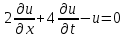 – c постоянными коэффициентами; – c постоянными коэффициентами;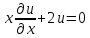 – с переменными коэффициентами. – с переменными коэффициентами.Если переменная в коэффициенте – то с переменными коэффициентами. Если хотя бы один с переменной - то с переменными коэффициентами. 5) Тип уравнения: – эллиптический (+) – параболический (0) – гиперболический (-) Если отсутствует хотя бы один член уравнения – то параболический ( 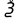 =0) =0)Если нет квадрата – параболический тип ( 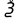 =1) =1)Даламбер для бесконечной струны 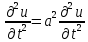 u(0,x) = f(x) – волна отклонения. ut(0,x) = F(x) – волна импульса u(t,x) = 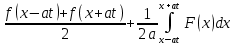 пример f(x) = 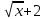 f(x-at) = 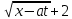 f(x+at) = 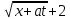 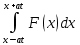 в данных пределах интегрирования х=х . в данных пределах интегрирования х=х .Фурье для 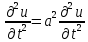 (0 (0u(0,x) = f(x) – волна отклонения. ut(0,x) = F(x) – волна импульса u(t,0) = u(t,l) = 0. Решается через фурье по синусу: U(t,x) = 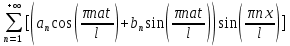 По синусу: an: 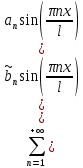 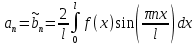 bn: 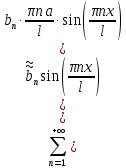 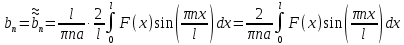 |
