ИЕРАРХИЧЕСКИЙ_ПОДХОД_FORMULALARNI_YOZDIRISH. Иерархический подход к получению моделей

• Название: Иерархический подход к получению моделей
• Дата: 01.04.2022
• Размер: 61.62 Kb.
• Имя файла: ИЕРАРХИЧЕСКИЙ_ПОДХОД_FORMULALARNI_YOZDIRISH.docx
• Тип: Документы; #433222

Иерархический подход к получению моделей.

Построение математических моделей с учетом всех значимых факторов не всегда бывает удобным и оправданным. Подход реализации «от простого — к сложному» в этом случае является более пред‑ почтительным. При данном подходе создается иерархия более полных моделей, обобщающих предыдущие модели как частные случаи. Математические модели нижнего уровня могут быть достаточно простыми, типовыми, допускающими широкую унификацию и использование набора готовых моделей. При иерархическом построении общей модели сложной системы задача оптимизации всей системы распадается на ряд частных задач оптимизации на различных уровнях. При этом общий критерий оптимизации разделяется на критерии для каждого уровня. Таким образом, задача большой размерности может быть сведена к ряду задач меньшей размерности. При этом следует учитывать взаимное влияние элементов и уровней, тогда возникает цепочка(иерархия) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качесве частного случая.

Построим такую иерархическую цепочку на примере модели многоступенчатой ракеты. Как было установлено в теме сохранения импульса, реальная одноступенчатая ракета неспособна развить первую космическую скорость. Причина этого - затраты горючего на разгон ненужной, отработавшей части структурной массы. Следовательно, при движении ракеты необходимо периодически избавляться от балласта. В практической конструкции это означает, что ракета состоит из нескольких ступеней, отбрасываемых по мере их использования.

Пусть m_i — общая масса i -й ступени,   - соответствующая структурная масса (при этом масса топлива равна величине   ),   - масса полезной нагрузки. Величины   и скорость истечения газов одинаковы для всех ступеней. Возьмем для определенности число ступеней n = 3. Начальная масса такой ракеты равна

m₀=m_p+m₁+m₂+m₃

Рассмотрим момент, когда израсходовано все топливо первой ступени и масса ракеты равна величине



Тогда по формуле (6) первоначальной модели скорость ракеты равна



После достижения скорости v₁ структурная масса   отбрасывается и включается вторая ступень. Масса ракеты в этот момент равна

m_p+m₂+m₃

Начиная с этого момента и до момента полного выгорания топлива второй ступени, ничто не мешает пользоваться уже построенной моделью, применив ее к рассматриваемому случаю. Все рассуждения о сохранении суммарного импульса и соответствующие выкладки остаются в силе (следует только учесть, что у ракеты уже есть начальная скорость v_i ). Тогда по формуле (6) после выгорания топлива во второй ступени ракета достигает скорости



Такие же рассуждения применимы и к третьей ступени ракеты. После отключения ее двигателей скорость ракеты равна



Эту цепочку нетрудно продолжить для любого числа ступеней и получить соответствующие формулы. В случае же n = 3 для окончательной скорости имеем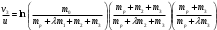



или, вводя величины


Получаем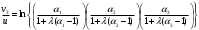



Данное выражение симметрично по отношению к величинам   , , и нетрудно показать, что его максимум достигается в симметричном случае, т.е. при  = = = . При этом для i = 3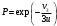
,

Произведение  = , как легко проверить, отношению m₀/m_p, или

Для многоступенчатой ракеты, аналогично, имеем
,	(11)

где n — число ступеней.

Проанализируем формулу (11). Примем v_n = 10,5 км/с, . Тогда для n = 2, 3, 4 получаем m₀ = 149 m_р, m₀ = 77 m_p, m₀ = 65 m_p соответственно. Это значит, что двухступенчатая ракета пригодна для выведения на орбиту некоторой полезной массы (однако при одной тонне полезного груза необходимо иметь ракету весом 149 тонн). Переход к третьей ступени уменьшает массу ракеты почти в два раза (но, конечно же, усложняет ее конструкцию), а четырехступенчатая ракета не дает заметного выигрыша по сравнению с трехступенчатой.

Построение иерархической цепочки позволило относительно просто прийти к этим важным выводам. Иерархия математических моделей часто строится и по противоположному принципу "от сложного к простому". В этом случае реализуется путь "сверху вниз" - из достаточно общей и сложной модели при соответствующих упрощающих предположениях получается последовательность все более простых (но имеющих уменьшающуюся область применимости) моделей.