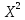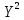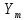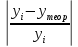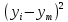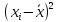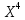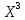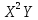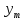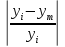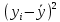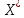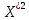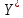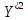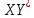7 вариант. Имеются данные о значениях признаков x, y
 Скачать 97.33 Kb. Скачать 97.33 Kb.
|
|
Имеются данные о значениях признаков x, y. Построить диаграмму рассеяния результирующей величины y и независимой переменной, сделать вывод о наличии и характере тренда. Построить линейную, квадратичную, гиперболическую и экспоненциальную модель. Наложить полученные линии тренда каждой модели на исходные точечные данные. Для каждой модели рассчитать среднюю ошибку аппроксимации и коэффициент детерминации. Сделать вывод о состоятельности полученных моделей. Оценить значимость уравнений регрессии с помощью F-критерия Фишера. Оценить значимость параметров линейной модели и коэффициента парной корреляции с помощью t-критерия Стьюдента.
Решение Построим точечную диаграмму рассеяния: 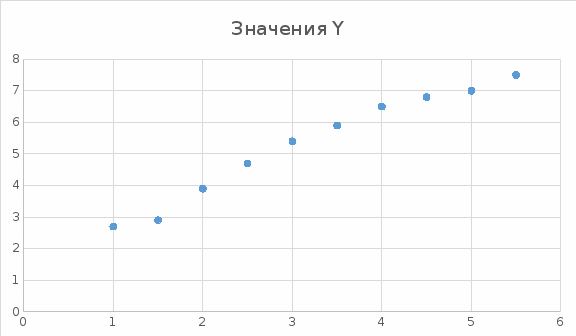 По диаграмме рассеивания мы видим, что лучше всего будет близок линейной или полиномиальной модели. Линейная модель. Найдем аппроксимирующую функцию в виде 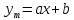 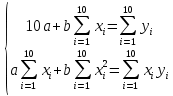
Получаем систему линейных уравнений: 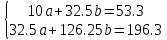 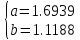 Уравнение регрессии имеет вид: 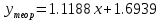 Добавим на диаграмму рассеяния линию линейного тренда 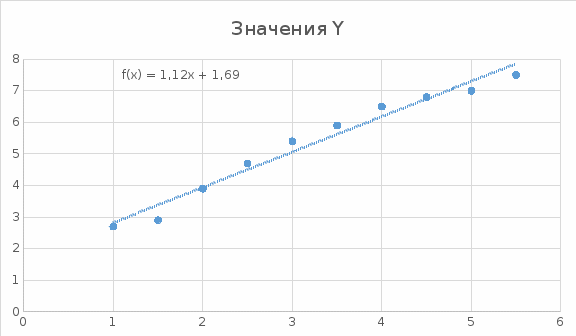 Вычислим среднюю ошибку аппроксимации:
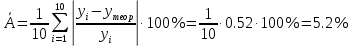 В среднем расчетные значения отклоняются от фактических на 5.2%. Ошибка аппроксимации 5.2% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. Вычислим коэффициент детерминации. Для этого сначала рассчитаем коэффициент парной корреляции: 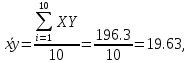 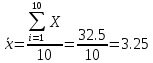 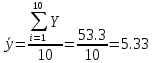 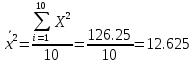 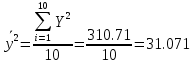 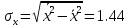 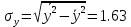 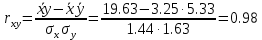 Тогда коэффициент детерминации 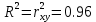 Так как коэффициент парной корреляции и коэффициент детерминации близки к единице, то связь между рассматриваемыми признаками тесная и прямая. Оценим значимость линейного уравнения регрессии с помощью критерия Фишера 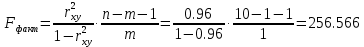  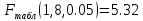 Так как Так как 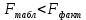 , то оцениваемые характеристики статистически значимы и надежны. , то оцениваемые характеристики статистически значимы и надежны.Проверим статистическую значимость параметров a,b и 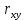 с помощью критерия Стьюдента. с помощью критерия Стьюдента. Вычислим стандартные ошибки параметров линейной регрессии и коэффициента корреляции
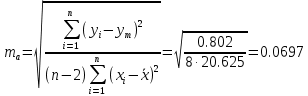 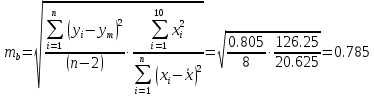  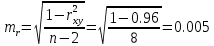 Далее рассчитываем фактические значения критерия  для оцениваемых коэффициентов регрессии и коэффициента корреляции для оцениваемых коэффициентов регрессии и коэффициента корреляции  : :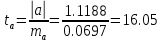  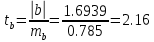 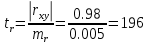 Критические значения Стьюдента 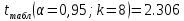 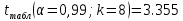 Параметр a и коэффициент 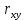 статистически значимы, так как статистически значимы, так как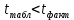 . Но для параметра b данное условие не выполняется, это значит что параметр статистически не значим и был сформирован случайно. . Но для параметра b данное условие не выполняется, это значит что параметр статистически не значим и был сформирован случайно.Квадратическая модель Модель будет принимать вид 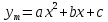 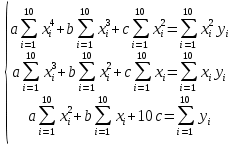
Для наших данных система имеет вид 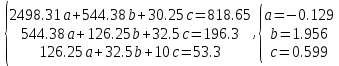 Уравнение квадратичной регрессии: 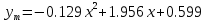 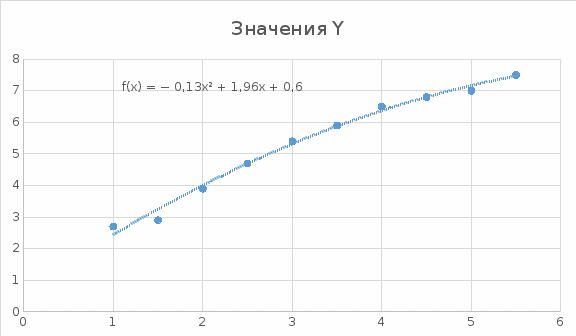 Вычислим среднюю ошибку аппроксимации
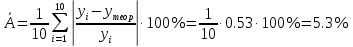 В среднем расчетные значения отклоняются от фактических на 5.3%. Ошибка аппроксимации 5.3% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. Вычислим коэффициент корреляции.
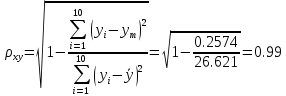 Тогда коэффициент детерминации: 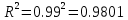 Полученный коэффициент корреляции близок к единице, что показывает о сильной и прямой связи между признаками X и Y. Оценим значимость квадратичного уравнения регрессии с помощью критерия Фишера. Для квадратичной модели m=2. 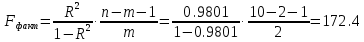 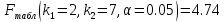 Так как 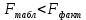 , то оцениваемые характеристики статистически значимы и надежны. , то оцениваемые характеристики статистически значимы и надежны.Гиперболическая модель Аппроксимирующая функция имеет вид 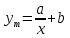 . Делая замену . Делая замену 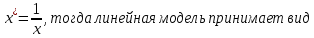 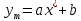 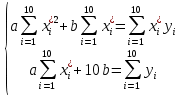
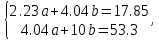 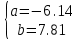 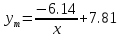 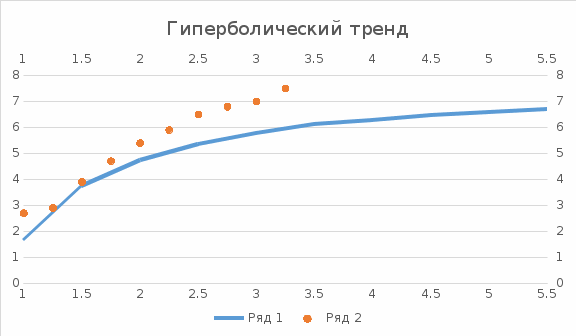 Вычислим среднюю ошибку аппроксимации
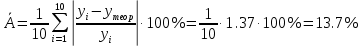 Найденное значение 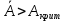 , значит гипотезу о гиперболической модели отвергаем. , значит гипотезу о гиперболической модели отвергаем.Экспоненциальная модель Аппроксимирующая функция имеет вид 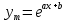 . Логарифмированием и заменой . Логарифмированием и заменой 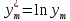 линеаризируем модель: линеаризируем модель: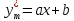 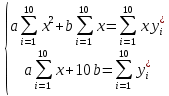
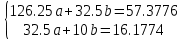 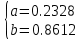 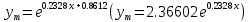 Добавим на диаграмму рассеяния линию экспоненциального тренда. 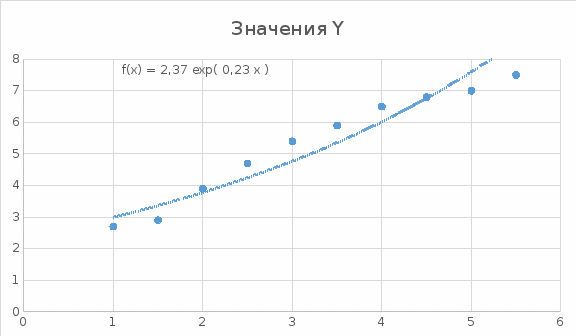 Вычислим среднюю ошибку аппроксимации
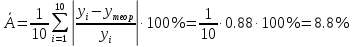 Найденное значение 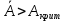 , значит гипотезу о экспоненциальной модели отвергаем. , значит гипотезу о экспоненциальной модели отвергаем.Вывод: В результате изучения и подбора модели для наших данных, мы получили, что лучше всего связь между признаками x и y описывает линейная и квадратичная модель. Сравнивая ошибки аппроксимации мы получаем, что можно брать в расчет и линейную, и квадратичную модель, так как значения ошибок приблизительно равны. |