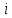задачи. антон. Имеются данные об объёмах продаж (Y, тыс шт.), затратах на рекламу (X1, тыс ден ед.) и затраты на сырье (X2, тыс ден ед.) для пяти предприятий за 20202021 года ()
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Имеются данные об объёмах продаж (Y, тыс.шт.), затратах на рекламу (X1, тыс. ден. ед.) и затраты на сырье (X2, тыс. ден. ед.) для пяти предприятий за 2020-2021 года (таблица 1). Таблица 1 - Исходные данные
Требуется построить однонаправленную модель с фиксированными эффектами зависимости объемов продаж У от факторов Х1 и Х2 . 2 Построение регрессионной модели по панельным данным и проверка адекватности модели в пакете STATISTICA Модель имеет вид 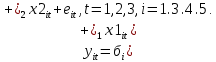 Исходные данные представим в пакете STATISTICA, изображено на рисунке 3. 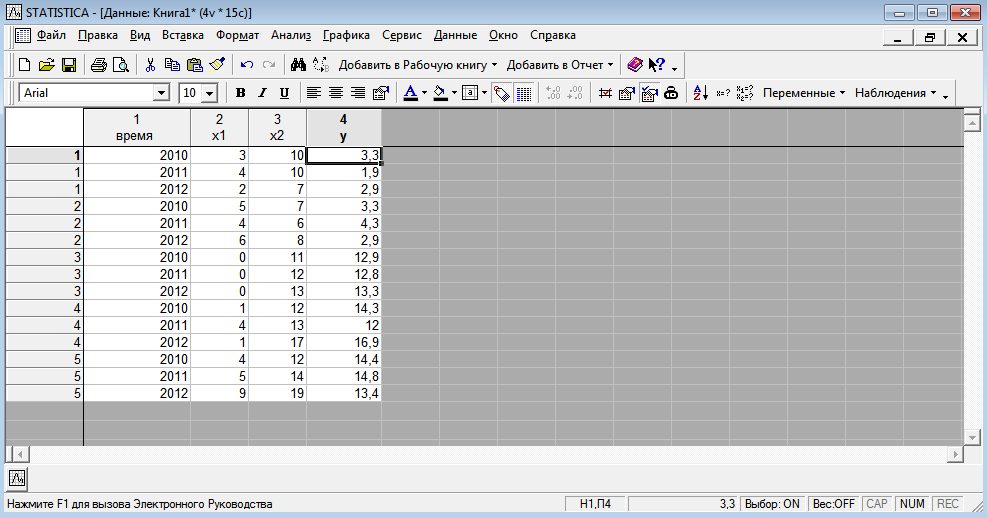 Рисунок 3 - Исходные данные Оценки коэффициентов данной модели находятся при помощи анализа STATISTICI, изображенном на рисунке 4. 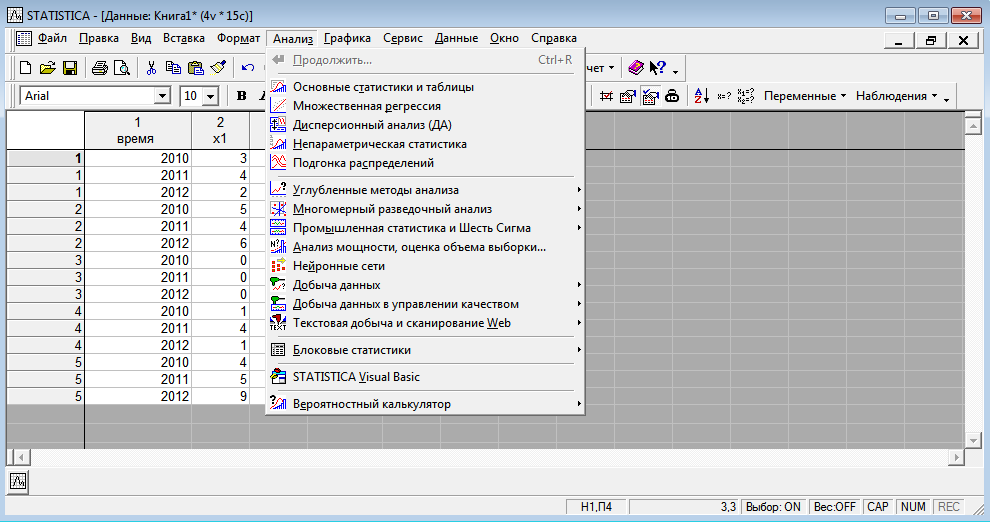 Рисунок 4 – Анализ STATISTICA Выбираем переменные для построения модели с фиксированными эффектами зависимости 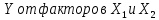 , изображенные на рисунке 5. , изображенные на рисунке 5.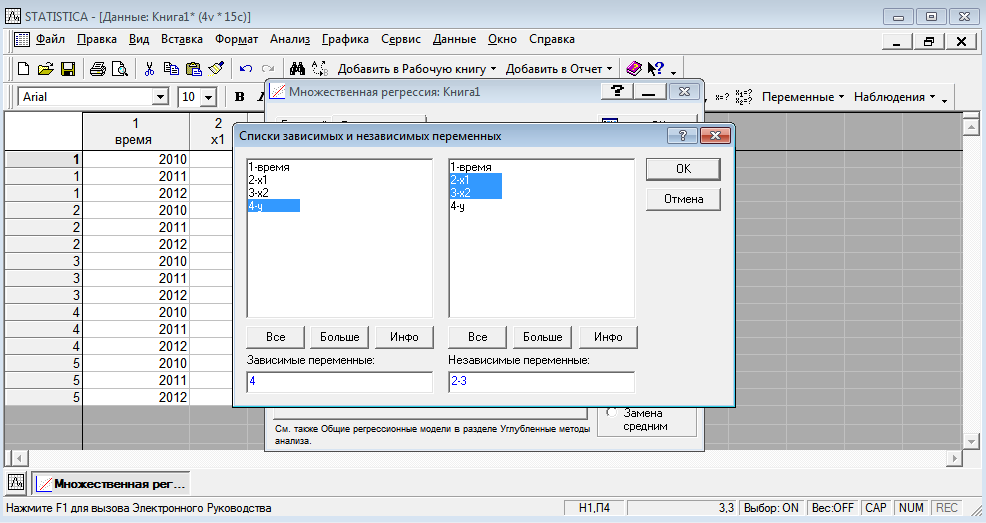 Рисунок 5 – Выбор переменных для построения регрессии регрессионная модель данный excel На стартовой панели отображен диалог определения оценивания модели, выбрав итоговую таблицу регрессии, были получены оценки коэффициентов, изображенные на рисунке 6. Так же данная модель проверена на адекватность, представлена на рисунке 7. 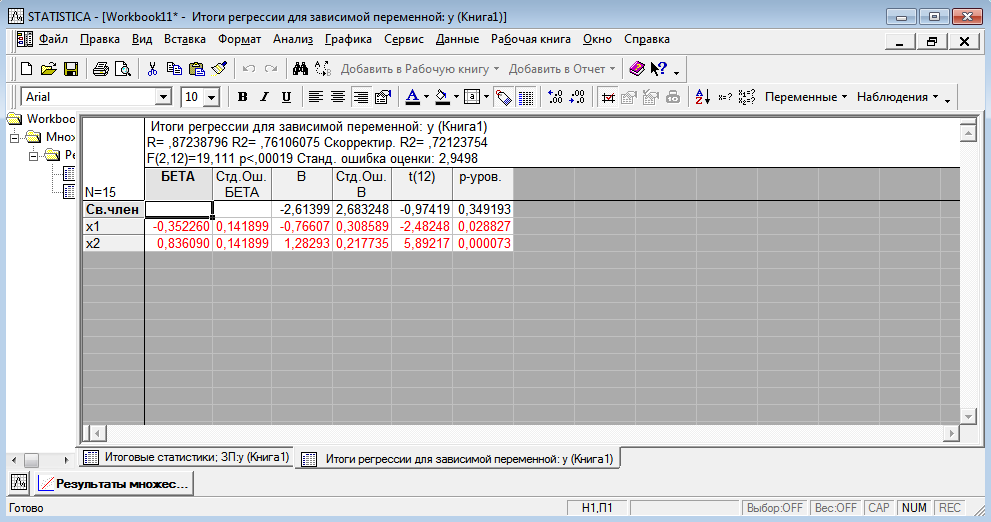 Рисунок 6 – Результаты оценки множественной линейной регрессии с фиктивными переменными В таблице приведены значения остатков для уравнения регрессии 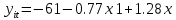 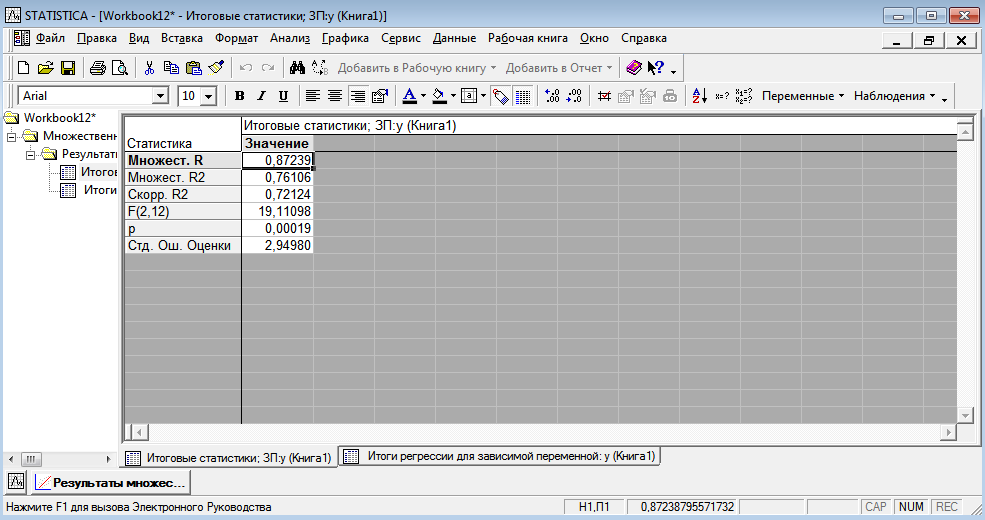 Рисунок 7 – Показатели адекватности уравнения регрессии с фиктивными переменными Согласно данным, приведенным на рисунке 6 и рисунке 7, модель статистически значима по F-критерию Фишера, при этом R2=0.76, что указывает на высокую адекватность модели. Задача 2 Необходимо исследовать зависимость заработной платы ( 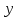 , тыс. руб.) от возраста ( , тыс. руб.) от возраста (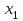 , лет) и стажа по данной специальности ( , лет) и стажа по данной специальности (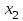 , лет), используя данные наблюдений, приведенные в таблице 1. Построить регрессионную модель , лет), используя данные наблюдений, приведенные в таблице 1. Построить регрессионную модель 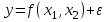 . Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет. . Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.Таблица 1 – Данные наблюдений
После ввода исходных данных в Excel, рассчитываются корреляционная матрица и значимость коэффициентов корреляции.
После спецификации модели производится параметризация. При помощи команды Сервис → Анализ данных → Регрессия создается еще один лист Excel c соответствующим именем. 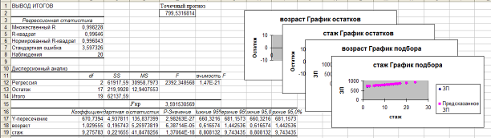 Далее производится верификация модели, в частности общее качество уравнения. Для этого вычисляется критическое значение. 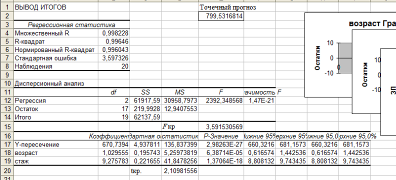 Далее находим нормальность распределения остатков с помощью пакета анализа данных.
Расчет критерия Пирсона производится с помощью пакета анализа. Также выводим график. 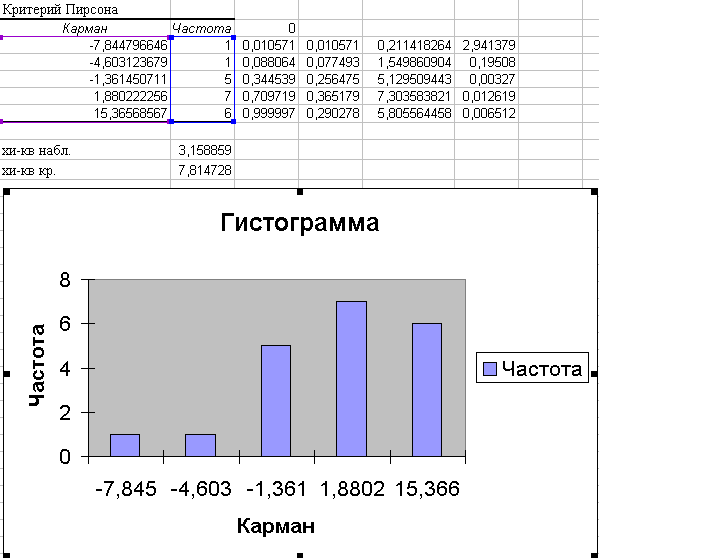 Рассмотрим значимость коэффициентов регрессии, вычислим критическое значение. 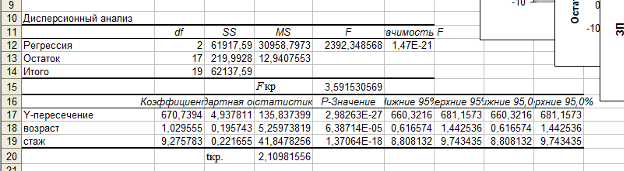 Проведем центрирование остатков на том же листе «Регрессия». 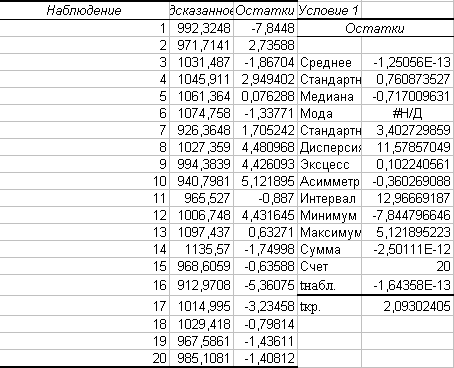 Гомоскедастичность (гетероскедастичность) остатков рассчитывается на отедльном листе «Усорвие2» с помощью формул массива и пакета анализа. 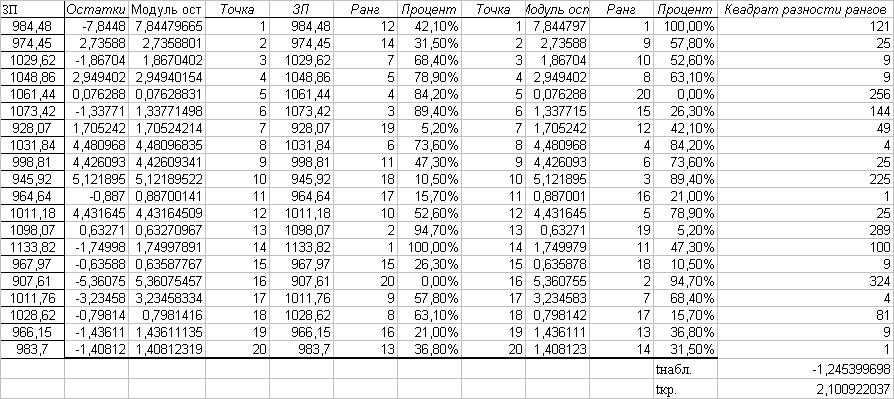 Автокорреляция остатков производится на листе «Регрессия», Условие3. 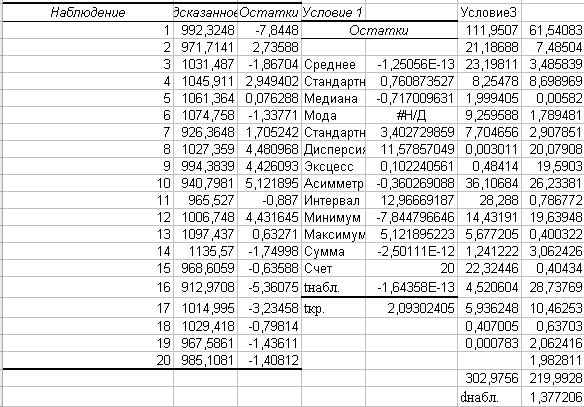 Если критерии Дарбина-Уотсона не дает ответа о наличии автокорреляции, то можно воспользоваться визуальным способом анализа графика зависимости остатков от номера наблюдения, построенного с помощью диаграммы. 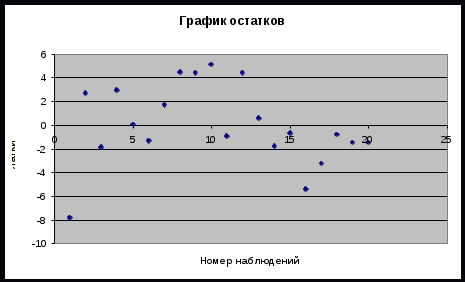 Для проведения анализа свойств модели рассмотрим мультиколлинеарность факторов: выявление зависимости объясняющих факторов. Для проверки гипотезы об отсутствии мультиколлинеарности используется статистика хи-квадрат с 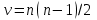 степенями свободы, наблюдаемое значение которой определяется по формуле степенями свободы, наблюдаемое значение которой определяется по формуле 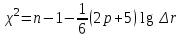 , где , где 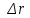 – определитель матрицы парных коэффициентов корреляции между факторами, n – количество наблюдений, p – число независимых переменных. Расссеты производятся на листе «Исходные данные». – определитель матрицы парных коэффициентов корреляции между факторами, n – количество наблюдений, p – число независимых переменных. Расссеты производятся на листе «Исходные данные».
Рассчитываем показатели эластичности. Для этого капируем коэффициенты стажа и возраста из листа «Регрессия».
Частные коэффициенты корреляции рассчитываются на том же листе «Исходные данные»
Для прогнозирования рассчитаем на листе «Регрессия» точечный прогноз для расчеты точечной оценки заработной платы при возрасте работника 35 лет и стаже работы 10 лет из условия задачи»  На новом листе «Интервальный_прогноз» произведем вычисления интервальной оценки прогноза, используя формулы ТАНСП(), МУМНОЖ(), МОБР(). 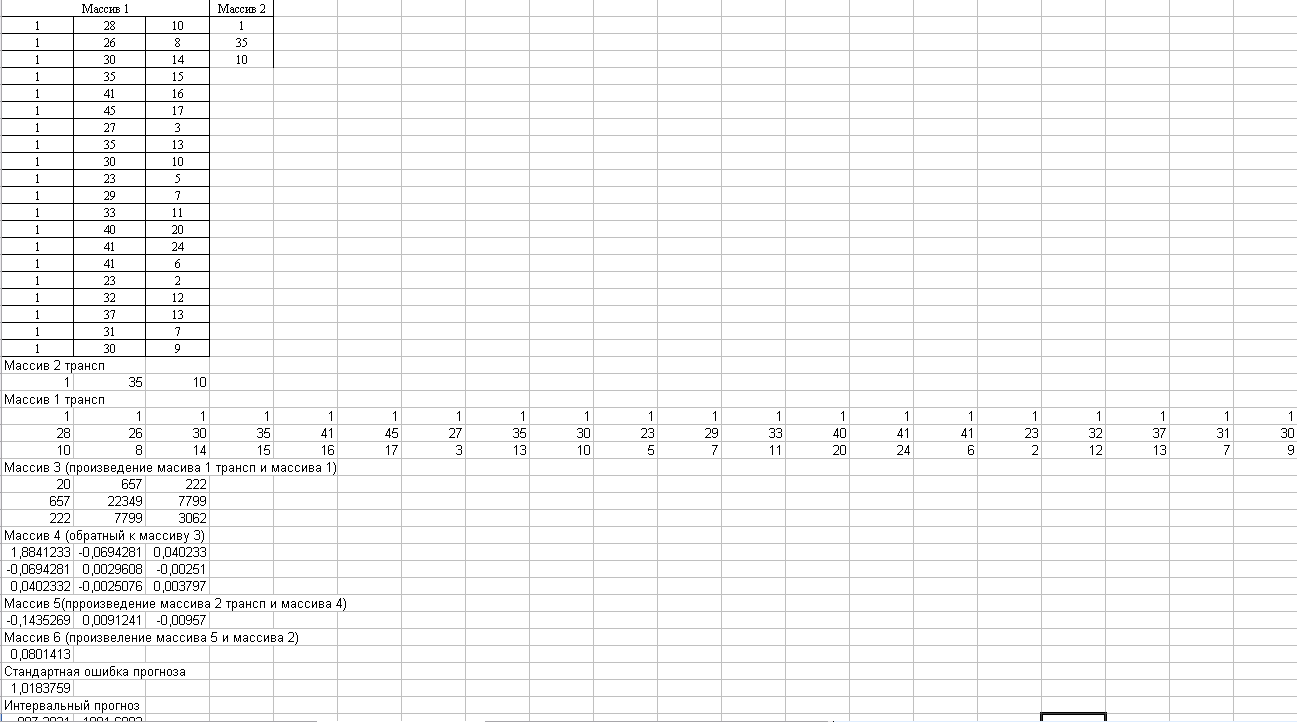 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||