Индивидуальная практическая работа 2(2) (2). Индивидуальная практическая работа Динамическое программирование
 Скачать 78 Kb.
|
Индивидуальная практическая работа 2. Динамическое программирование.Указания по выбору вариантаВыбор вариантов контрольного задания осуществляется студентом самостоятельно на основании двух последних цифр номера зачетной книжки (в каждом задании предусмотрено 20 вариантов). Варианты Задача (1-2) о распределении средств между предприятиями Планируется деятельностьnпромышленныхпредприятий на очередной год. Начальные средства: s0 . Размеры вложений в каждое предприятие кратныx . Средства x , выделенные предприятию i приносят в конце года прибыльfi (x), i = 1,2. … n. Прибыльfi (x) не зависит от вложения средств в другие предприятия. Прибыль от каждого предприятия выражается в одних и тех же условных единицах; суммарная прибыль равна сумме прибылей от каждого предприятия. Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей. Задача (3-4) об оптимальном распределении ресурсов между отраслями на n лет Планируется деятельность производства на n лет. Начальные ресурсы: s0 . Средства x , вложенные в отрасль 1 в начале года, дают в конце года прибыль f1(x) и возвращаются в размере 1(x)< x. Для отрасли 2 аналогично - f2(x) и 2 (x)< x. В конце года все возвращенные средства заново перераспределяются между этими отраслями, новые средства не поступают, прибыль в производство не вкладывается. Требуется распределить имеющиеся средства между двумя отраслями производства на лет так, чтобы суммарная прибыль от обеих отраслей за n лет была максимальной. В задачах 1-2 найти оптимальное распределение средств между предприятиями при условии, что прибыль f(x), полученная от каждогопредприятия, является функцией от вложенных в него средств x, вложения кратны x , а функция f(x) заданы таблично. Задача 1
s0 = 9, x = 1, n= 4(3) Задача 2.
s0 = 5, x = 1, n= 4 В задачах 3-4 найти оптимальное распределение ресурсов s0 между двумя отраслями производства в течение n лет, если даны функции доходов f1(x) f2(x) для каждой отрасли, функции возврата 1(x) и 2 (x). По истечении года только все возвращенные средства перераспределяются, доход в производство не вкладывается Задача 3. s0= 40000 ед.; n= 4; f1(x)=0.4 x; f2(x)=0.3 x;1(x)=0.5 x;2 (x)=0.8 x Задача 4. s0= 10000 ед.; n= 4; f1(x)=0.4 x2; f2(x)=0.5x;1(x)=0.75 x;2 (x)=0.3 x Варианты индивидуального задания
Методические указанияДинамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Показатель эффективности данной управляемой операции – целевая функция – зависит от начального состояния и управления Z = F(0,X). Целевая функция является аддитивной от показателей эффективности Zn каждого шага Z= 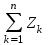 = 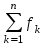(k–1,xk), k = 1, 2,…,nи управления состоянием n= k(k–1, xk), k =1, 2,…,n. Задача пошаговой оптимизации (задача ДП) формулируется так: определить такое допустимое управление X (Х1, Х2,…,Хn), переводящее систему Sиз состояния 0 в состояние 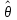 , при котором целевая функция Zпринимает наибольшее (наименьшее) значение.Вычислительная схема ДП связана с принципом оптимальности Беллмана и использует рекуррентные соотношения. Zk*(k–1) = 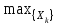 {fk(k–1, Xk)+ Zk+1*(k)}, k=1,2,…,n–1. (2.1) Согласно принципу оптимальности, Xkвыбирается из условия максимума этой суммы. В результате условной оптимизации получаются две последовательности: – Zn*(n–1), Zn–1*(n–2),…,Z2*(1), Z1*(0) – условные максимумы целевой функции на последнем, на двух последних,…, на n шагах; – Xn*(n–1), Xn–1*(n–2),…,X2*(1), X1*(0) – условные оптимальные управления на n–м, (n–1) –м,…,1–м шагах. 2.1. Задача о распределении средств между предприятиями Планируется деятельность четырех промышленных предприятий на очередной год. Начальные средства: 0 = 5 у.е. Размеры вложения в каждое предприятие кратны 1 у.е. Средства x, выделенные k–му предприятию (k = 1, 2, 3, 4), приносят в конце года прибыль fk(x). Функции fk(x) заданы таблично. Таблица 2.1
Будем считать, что: прибыль fn(x) не зависит от вложений средств в другие предприятия; прибыль от каждого предприятия выражается в одних и тех же условных единицах; суммарная прибыль равна сумме прибылей, полученных от каждого предприятия. Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей. Решение. Обозначим через xkколичество средств, выделенных k–му предприятию. Суммарная прибыль равна Z= 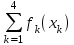 . (2.2)Переменные xk удовлетворяют ограничениям 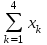 =5, xk 0, k = 1, 2, 3, 4. (2.3)Требуется найти переменные x1, x2,, x3,, x4, удовлетворяющие (6.3) и обращающие в максимум функцию (6.2). Схема решения задачи ДП: процесс решения распределения средств 0 = 5 можно рассматривать как четырехшаговый, номер шага совпадает с номером предприятия; выбор переменных x1, x2, x3, x4– управление соответственно на 1, 2, 3 и 4 шагах; 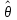—конечное состояние процесса распределения – равно 0, т.к. все средства должны быть вложены. Схема распределения показана на рис. 6.1. Рис. 2.1 Уравнения состояний в данной задаче имеют вид k = k–1– xk, k=1, 2, 3, 4, где k – параметр состояния – количество средств, оставшихся после k–го шага, т.е. средства, которые остается распределить между оставшимися 4–k предприятиями. Zk*(k–1) – условная оптимальная прибыть, полученная от k–го, (k+1)–го, …, 4 предприятий, если между ними оптимальным образом распределялись средства k–1. Допустимые управления на k–м шаге удовлетворяют условию 0 хkk–1. Уравнения Беллмана имеют вид: к = 4, 4=0 Z4*(3)=max f4(x4), 0 x43; Z3*(2)=max {f3(x3) + Z4*(3)}, 0 x32; Z2*(1)=max {f2(x2) + Z3*(2)}, 0 x21; Z1*(5)=max {f1(x1) + Z2*(1)}, 0 x3 5. 4 шаг (k = 4). В табл. 2.1 f4(x) прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4–е предприятие. Для возможных значений 3 = 0, 1, 2, 3, 4, 5 получим Z4*(3)=f4(3) и x4*(3)=3. Таблица 2.2
3 шаг (k = 3). Делаем все предположения относительно остатка средств 2 к 3 шагу, т.е. после выбора x1 и x2. 2 = 0, 1, 2, 3, 4, 5 (0 – все средства отданы 1 и 2–му предприятиям, 5 – 1–е и 2–е предприятия ничего не получили и т.д.) В зависимости от этого выбираем 0 x32, находим 3=2 – x3и сравниваем для разных x3при фиксированном 2 значения суммы f3(x3)+Z4*(3). Для каждого 2наибольшее из этих значений есть Z3*(2) – условная оптимальная прибыль, полученная при оптимальном распределении 2 между 3–м и 4–м предприятиями. Оптимизация приведена в табл. 6.2 при k = 3. 2 шаг. Условный оптимум приведен в той же таблице и для k = 2. Для всех возможных значений 2значения Z2*(1) и Х2*(1) находятся в столбцах 8 и 9 соответственно; первые слагаемые в столбце 7 – значения f2(x2) взяты из табл. 6.2, а вторые слагаемые взяты из столбца 5 табл. 6.2 при 2=1–x2. 1 шаг. Условный оптимум приведен и для k = 1 при 0 = 5. Итак, максимум суммарной прибыли Zmax=Z1*(5)=24 у. е. при x1*=x1*(5)=1 1*=5–1=4 x2*=x2*(4)=2 2*=4–2=2 x3*=x3*(2)=1 3*=2–1=1 x4*=x4*(1)=3*=1. Выделение средств различным предприятиям: 1–му выделена 1 у. е. 2–му выделены 2 у. е. 3–му выделена 1 у. е. 4–му выделена 1 у. е. Замечания. Решение четырехмерной задачи на определение условного экстремума сведено фактически к решению четырех одномерных задач: на каждом шаге определялась одна переменная х. Из разобранной задачи видно, что метод ДП безразличен к виду и способу задания функции: fk(x) были заданы таблично, поэтому Zk*() и Хk*() принимали дискретные значения, представленные в таблице. Достоинством метода является возможность анализа решения на чувствительность к изменению 0 и n. Проведенные расчеты можно использовать для изменившихся начального состояния 0 и числа шагов n. Например, пусть в задаче произошло уменьшение начальных средств на 1 у.е. Для 0 = 4 достаточно в таблицу добавить расчеты при k= 1. Получаем в этом случае Zmax = 21 у.е. при распределении: x1*=11*=4–1=3 x2*=1, или x2*=2 2*=3–1=2, или 2*=3–2=1 x3*=1, или x3*=0 3*=2–1=1, или3*=1–0=1, x4*=1. В результате найдены два оптимальных решения: (1,1,1,1) и (1,2,0,1). Если начальные средства увеличились, например, на 1 у.е., 0 = 6, а функции прибыли fk(x) остались прежними, то в таблицу достаточно добавить раздел для 0 = 6 при k= 3, 2, 1; этот фрагмент расчетов помещен в табл. 2.3. Таблица 2.3
Получаем Zmax=27 у.е. при распределении: x1*=11*=6–1=5 x2*=12*=5–1=4 x3*=0 3*=4–0=4 x4*=4. Оптимальное решение (1,1,0,4). Если принято решение распределить средства 0 = 5 между 2–, 3– и 4–м предприятиями, то задача уже решена. В разделе k= 2 табл. 6.2 находим Zmax=Z2*(5)=19 при условии, что x2*=1, x3*=0, x4*=4. Наконец, если увеличилось количество предприятий (число шагов), то схему можно дополнить, присоединяя шаги с номерами k= 0,–1,… и т.д. Например, пусть средства в размере 6 у.е. распределяются между пятью предприятиями. Функция прибыли для пятого предприятия задана формулой f(x) = 3x+1, если х и f(0) = 0. Присвоим 5–му предприятию номер k= 0, тогда х0 = 0 – средства, выделенные этому предприятию. Обозначим через Z0*(6) оптимальную прибыль, полученную от пяти предприятий: Z0*(6)= Z3*(2)=max {f0(x0) + Z1*(1)}, 0 x0 6, а 1= 6 – х0. Условная оптимизация 0–го шага дана в табл. 2.4. Таблица 2.4
Следовательно, Zmax=28, а оптимальных решений четыре: (1,1,2,1,1), (2,1,1,1,1), (2,1,2,0,1), (3,1,1,0,1). ▼ 2.2. Задача об оптимальном распределении ресурсов между отраслями на n лет Планируется деятельность двух отраслей производства на n лет. Начальные ресурсы 0. Средства х, вложенные в 1–ю отрасль в начале года, дают в конце года прибыль f1(x) и возвращаются в размере q1(x) Требуется распределить имеющиеся средства 0 между двумя отраслями производства на n лет так, чтобы суммарная прибыль от обеих отраслей за n лет оказалась максимальной. Необходимо: построить модель ДП для задачи и вычислительную схему; решить задачу при условии, что 0 = 10000 у.е., n = 4, f1(x) = 0,6x, q1(x) = 0,7x, f2(x) = 0,5x, q2(x) = 0,8x. Решение. Процесс распределения средств между двумя отраслями производства разворачивается во времени, решения принимаются в начале каждого года, следовательно, осуществляется деление на шаги: номер шага – номер года. Управляемая система – две отрасли производства, а управление состоит в выделении средств каждой отрасли в очередном году. Параметры состояния к началу k–го года — k–1 (k = 1,…,n) – количество средств, подлежащих распределению. Переменных управления на каждом шаге две: хk — количество средств, выделенных 1 отрасли, и yk — 2 отрасли. Но так как все средства k–1 распределяются, то уk = k–1 – xk, и поэтому управление на k–м шаге зависит от одной переменной xn, т.е. Хk (хk, k–1 – xk). Уравнения состояний выражают остаток средств, возвращенных в конце k–го года k = q1(xk) + q2(k–1 – xk). Показатель эффективности k–го шага — прибыль, полученная в конце k–го года от обеих отраслей: f1(xk) + f2(k–1 – xk). Суммарный показатель эффективности — целевая функция задачи — прибыль за n лет: Z = 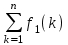 + f2(k-1 - xk).Пусть Z*k(k–1) — условная оптимальная прибыль за n – k + 1 лет, начиная с k–го года до n–го года включительно, при условии, что имеющиеся на начало k–го года средства k–1 в дальнейшем распределялись оптимально. Тогда оптимальная прибыль за n лет Zmax = Z*1(0). Уравнения Беллмана имеют вид: Z*n(n–1) = max {f1(xn) + f2(n–1 – хn)},0 хnn–1; Z*k(k–1) = max {f1(xk) + f2(k–1 – хk) + Z*k+1(k)} , 0 хkk–1, (k = n–1, n–2, …, 2). Используем конкретные данные. Уравнение состояний примет вид k = 0,7xk + 0,8(k–1 – xk) или k = 0,8k–1 –0,1xk. Целевая функция k–го шага 0,6xk + 0,5(k–1 – xk) = 0,1xk + 0,5k–1. Целевая функция задачи Z = 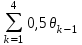 + 0,1xk..Z*4(3) = max {0,53 + 0,1x4} 0 х43; Z*k(k–1) = max {0,1xk + 0,5k–1 + Z*k+1(k)}, 0 хkk–1. Проводим условную оптимизацию. 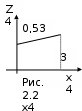 4 шаг. Используем уравнение Z*4(3) = max {0,53 + 0,1x4},0 х43. Обозначим Z4 = 0,1х4 + 0,53; Z4 линейная, возрастающая, так как угловой коэффициент 0,1 больше нуля. Поэтому максимум достигается на конце интервала [0;3]. Следовательно, Z*4(3)= 0,63 при х*4(3)= 3. 3 шаг. Уравнение Z*3(2) = max {0,1x3 + 0,52 + 0,63}, 0 х32. Найдем 3 из уравнений состояний: 3 = 0,82 – 0,1x3 и, подставив его выражение в правую часть уравнения, получим Z*3(2) = max {0,1x3 + 0,52 + 0,6(0,82 – 0,1x3)} = max {0,04x3 + 0,982}, 0 х32. Как и в предыдущем случае, максимум достигается при х3=2; т.е. Z*3(2)= 1,022 при х*3(2)= 2. 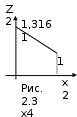 2 шаг. Из уравнения состояния: 2 = 0,81 – 0,1x2. Уравнение при k=2 примет вид Z*2(1) = max {1,3161 – 0,002x2}, 0 х21. Линейная функция Z*2 = 1,3161 – 0,002x2 относительно х2 убывает на отрезке [0;1], и поэтому ее максимум достигается при х2=0: Z*2(1)= 1,3161 при х*2(1)= 0. 1 шаг. 1 = 0,81 – 0,1x1. Уравнение при k=1 имеет вид Z*1(0) = max {1,55280 – 0,031x1}, 0 х10. Как и в предыдущем случае, максимум достигается в начале отрезка, т.е. Z*1(0)= 1,55280 при х*1(0)= 0. На этом условная оптимизация заканчивается. Используя ее результат и исходные данные, получим Zmax = Z*1(10000), Zmax = 15528. х*1 = 0, у*1 = 0 = 10000 *1 = 0,8*10000 –0,1*0 = 8000 х*2 = 0, у*2 = 8000 *2 = 0,8*8000 –0,1*0 = 6400 х*3 = 6400, у*3 =0 *3 = 0,8*6400 –0,1*6400 = 4480 х*4 = 4480, у*4 =0. Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 10000 у.е., равна 15528 у.е. при условии, что 1 отрасль получает по годам (0;0;6400;4480), а 2 отрасль – соответственно (10000;8000;0;0). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||