ИДЗ. Индивидуальное домашнее задание. Вариант Задача Материальная точка движется согласно уравнению r(t) a (I
 Скачать 26.45 Kb. Скачать 26.45 Kb.
|
|
Индивидуальное домашнее задание. Вариант 3. Задача 3. Материальная точка движется согласно уравнению r(t) = A (i cosωt + j sinωt), где A = 0.5 м, ω= 5  . Изобразите на рисунке траекторию движения. Определите модуль скорости |v| и модуль нормального ускорения | . Изобразите на рисунке траекторию движения. Определите модуль скорости |v| и модуль нормального ускорения |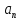 |. |.Задача 53. На барабан радиуса R = 0.5 м намотана нить, барабан вращается вокруг горизонтальной оси, проходящей через его ось симметрии, под действием груза, подвешенного к нити. Груз движется с постоянным ускорением a = 5  . Найти угловое ускорение вращения барабана и полное ускорение точек на его поверхности через ∆t = 1 c после начала вращения барабана. . Найти угловое ускорение вращения барабана и полное ускорение точек на его поверхности через ∆t = 1 c после начала вращения барабана.Задание 63. Две пружины жесткостью 3⋅ 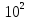 Н/м и 6⋅ Н/м и 6⋅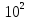 Н/м соединены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина растянута на 3 см. Определить также коэффициент жесткости системы двух пружин. Н/м соединены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина растянута на 3 см. Определить также коэффициент жесткости системы двух пружин.Вопросы к лабораторной работе №3. Вопрос 11. Дайте определение декремента затухания и логарифмического декремента затухания. Ответ:
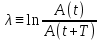 Вопрос 22. Докажите, что решением уравнения 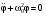 является функция является функция 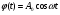 . .Ответ: 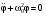 - уравнение движения тела без учета сил трения в подвесе. - уравнение движения тела без учета сил трения в подвесе.Трение в подвесе создает тормозящий момент, пропорциональный скорости движения маятника 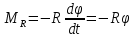 , где R – коэффициент сопротивления. С учетом сил трения уравнение движения маятника принимает вид , где R – коэффициент сопротивления. С учетом сил трения уравнение движения маятника принимает вид в котором коэффициент  называют коэффициентом затухания. Решение этого уравнения при называют коэффициентом затухания. Решение этого уравнения при 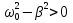 описывает затухающие колебания маятника и имеет вид (при условии, что диск повернут относительно положения равновесия и отпущен без толчка) описывает затухающие колебания маятника и имеет вид (при условии, что диск повернут относительно положения равновесия и отпущен без толчка)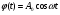 , ,а следовательно является решением уравнения 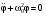 |
