Сапронова_151_пр.р.6. Информатика
 Скачать 32.16 Kb. Скачать 32.16 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Южно-Уральский государственный университет» (Национальный исследовательский университет) Разветвляющиеся алгоритмические структуры ОТЧЕТ о практической работе № 6 по дисциплине «Информатика» Выполнил студент группы ПЗ-151 ___________/Сапронова О.А. (подпись) ____________________2021г. (дата) Отчет принял, (должность) __________/Л.Н. Паламарчук/ (подпись) ____________________2021 г. (дата) Челябинск 2021 Цель работы: Научиться строить разветвляющиеся алгоритмы, записывать алгоритмы в виде блок-схемы и на алгоритмическом языке. Ход работы: Задание №21 21) Даны действительные числа a, b, c ( a 0 ). Выяснить, имеет ли уравнение ax2 bx c 0, действительные корни. Если действительные корни имеются, то найти их. Решение: Из алгебры известно, что: Квадратное уравнение ax2 + bx + c = 0, выражение D = b2 – 4ac – дискриминант: – если D > 0, имеет два решения: – если D = 0, имеет единственное решение: – если D < 0, не имеет действительных решений. Следовательно, нам необходимо вычислить дискриминант (заведем для него вещественную переменную d типа real) и в зависимости от его значения организовать ветвления. Сначала нужно проверить, имеет ли уравнение действительные решения (для решений заведем переменные x1 и x2 типа real). Если да, и если дискриминант не равен нулю, то вычисляем оба решения по формулам, а если дискриминант равен нулю, то вычисляем единственное решение. Если же действительных решений нет, выводим текстовое сообщение об этом. Основной алгоритм можно проиллюстрировать следующей блок-схемой: 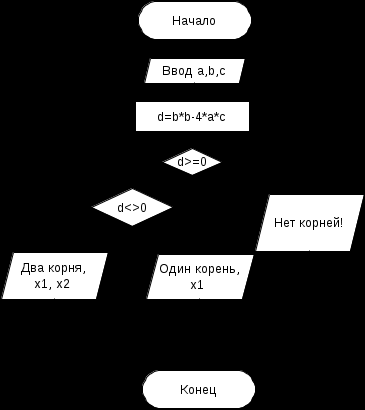 Текст программы: program Korni; uses crt; var a, b, c, d, x1, x2: real; begin clrscr; write('Введите 3 коэффициента a, b, c, разделяя знаком пробела: '); readln(a, b, c); d := b * b - 4 * a * c; if d >= 0 then begin if d <> 0 then begin x1 := (-b + sqrt(d)) / 2 * a; x2 := (-b - sqrt(d)) / 2 * a; writeln('Два различных корня, x1 = ', x1:4:2, ', x2 = ', x2:4:2) end else begin x1 := -(b / 2 * a); writeln(' Один корень x = ', x1:4:2) end end else begin writeln('Нет корней!'); end end. Пример:  |
