ответ на контрольный вопрос 3. Институт дополнительного профессионального образования
 Скачать 109.5 Kb. Скачать 109.5 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» ИНСТИТУТ ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Программа профессиональной переподготовки «Химическая технология природных энергоносителей и углеродных материалов» Ответ на контрольный вопрос по направлению Моделирование в химической технологии и расчет реакторов: Расчет параметров математической модели на основе пассивного эксперимента методом наименьших квадратов. Достоинства и недостатки метода. Проверил: Уфа — 2020 1 Моделирование и экспериментальные измерения Одной из главных задач эксперимента является получение и проверка математической модели объекта, описывающей в количественной форме взаимосвязи между входными и выходными параметрами объекта. Входные параметры, которые могут быть изменены, называют факторами. Для каждого фактора до измерения устанавливается область определения, которая может быть непрерывной и дискретной. Часто непрерывная область определения искусственно дискретизируется. В теории планирования эксперимента объект исследований принято представлять в виде «черного ящика», а его математическая модель описывает функциональные связи между входными и выходными параметрами. Главными требованиями, предъявляемыми к математическим моделям объектов, являются удобство математического использования и интерпретируемость модели. Кроме того, всегда должны быть обозначены пределы применимости модели. Если эти требования не выполняются, то при использовании и экспериментальной проверке моделей неизбежно возникают методические погрешности, и погрешности адекватности, которые будут рассмотрены в следующей главе. Можно выделить следующие задачи проверки моделей (рис.1.1): 1. Построить «черный ящик», который будет нужным образом откликаться на заданное входное воздействие. 2. Имея «черный ящик», зная входные и выходные сигналы, получить (смоделировать) его содержимое.  Рис. 1.1 Суть процесса моделирования можно пояснить на примере анализа электронной схемы, в результате которого будут получены определенные выходные сигналы. Можно проверить модель, собрав экспериментальную схему и сняв реальные выходные сигналы. При этом неизбежны расхождения между сигналами модельными и реальными. Чтобы выяснить причины расхождения, необходимы эксперименты с отдельными элементами схемы. Необходимая корректировка модели может быть выполнена следующим образом: 1. Проверка расхождений — экспериментальная проверка характеристик всех элементов и их сравнение с модельными. 2. Исправление характеристик отдельных элементов в исходной модели. 3. Сопоставление полученных зависимостей с экспериментальными (исходными). Таким образом, построение и проверка модели, адекватно описывающей работу электронной схемы, в общем случае требует очень большого количества экспериментальных измерений. Планирование эксперимента позволяет оптимизировать число измерений. Например, электронная схема состоит из транзисторов, резисторов, конденсаторов и катушек индуктивности. Если номинальные значения пассивных электронных элементов (резисторов, конденсаторов и т.д) совпадают с их реальными значениями с необходимой точностью, то несовпадение между модельными и реальными сигналами чаще всего возникает из-за несоответствия реальных рабочих характеристик активных элементов (транзисторов, микросхем и т.д.). Поэтому опытные схемотехники подвергают проверке лишь отдельные узлы схемы, по сути интуитивно планируя эксперимент исходя из своего опыта и используя априорную информацию. [2] 2 Пассивный эксперимент Теория предполагает, что эксперимент может быть пассивным и активным. При пассивном эксперименте информация об исследуемом объекте накапливается путем пассивного наблюдения, то есть информацию получают в условиях обычного функционирования объекта. Активный эксперимент проводится с применением искусственного воздействия на объект по специальной программе. При пассивном эксперименте существуют только факторы в виде входных контролируемых, но неуправляемых переменных, и экспериментатор находится в положении пассивного наблюдателя. Задача планирования в этом случае сводится к оптимальной организации сбора информации и решению таких вопросов, как выбор количества и частоты измерений, выбор метода обработки результатов измерений. Наиболее часто целью пассивного эксперимента является построение математической модели объекта, которая может рассматриваться либо как хорошо, либо как плохо организованный объект. В хорошо организованном объекте имеют место определенные процессы, в которых взаимосвязи входных и выходных параметров устанавливаются в виде детерминированных функций. Поэтому такие объекты называют детерминированными. Плохо организованные или диффузные объекты представляют собой статистические модели. Методы исследования с использованием таких моделей не требуют детального изучения механизма процессов и явлений, протекающих в объекте. Примером пассивного эксперимента может быть анализ работы схемы, которая не имеет входов, только выходы, и повлиять на ее работу невозможно. Хорошим примером пассивного эксперимента с диффузным объектом являются измерения метеорологических параметров (температуры, скорости ветра и т.д.) при природных катаклизмах. 3 Планирование эксперимента. Метод наименьших квадратов позволяет получить описание объекта по любым данным, лишь бы матрица системы нормальных уравнений была невырожденной. В реальных условиях технологический процесс все время испытывает случайные колебания режима. Сегодня значения контролируемых факторов – несколько иные, чем вчера, а завтра будут еще немного другими. Нельзя ли каждое изменение режима рассматривать как эксперимент, и, обработав совокупность таких «экспериментов» методом наименьших квадратов, получить описание процесса, а затем использовать это описание для управления и оптимизации? Такой подход получил название пассивного эксперимента. Достоинство пассивного эксперимента – отсутствие затрат на опыты: данные получаются «сами собой». Но надежды, возлагавшиеся на этот метод, в большинстве случаев не оправдались. Анализ неудач пассивного эксперимента выявил несколько их причин. Во-первых, в нормальных условиях колебания режима малы, опытные точки находятся близко одна к другой. Хорошо известно, что чем ближе опытные точки, тем сильнее влияют на описание случайные ошибки. Действительно, различия в получаемых значениях отклика при этом малы, и эти малые различия плохо выделяются на фоне шума – случайных ошибок. Во-вторых, в пассивном эксперименте факторы сильно коррелированы. Это делает крайне ненадежным анализ влияния отдельных факторов – всегда может оказаться, что влияет не данный фактор, а другой, с ним коррелированный. В-третьих, сами значения факторов в производственных условиях часто измеряются с заметными ошибками; поэтому применение метода наименьших квадратов в его обычном варианте становится некорректным. В связи с этим в теории эксперимента любой эксперимент, при планировании которого не учтено влияние плана эксперимента на статистические свойства получаемых оценок, часто называют пассивным. Ему противопоставляют активный эксперимент, в основе которого лежит планирование эксперимента.[3] 4 Расчет параметров математической модели на основе пассивного эксперимента методом наименьших квадратов. При исследовании объектов химической технологии во многих случаях связь между выходным параметром и факторами аппроксимируется линейной зависимостью. В простейшем случае уравнение имеет вид: yM=b0+b1x1 (1.1) В результате идентификации объекта мы должны найти значения коэффициентов b0 и b1. При отсутствии помех доля определения неизвестных коэффициентов достаточно двух опытов. Y1= b0+b1x11 (1.2) y2= b0+b1x12 Однако на практике для учета случайных факторов проводят большее число опытов N>2. Система уравнений (2.3) пополняется дополнительными уравнениями. y1= b0+b1x11 (1.2) y2= b0+b1x12 yN= b0+b1x1N В этом случае полученные экспериментальные данные необходимо усреднить. Метод наименьших квадратов (МНК).Самым распространенным, хотя и не единственным методом усреднения является метод наименьших квадратов (МНК). Суть метода МНК заключается в соблюдении требования минимума суммы 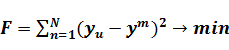 (1.3) (1.3)Или с учетом (1.1) 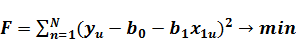 (1.4) (1.4)т.о. процедура нахождения коэффициентов уравнения регрессии сводится к задаче нахождения минимума функции. Необходимым условием минимума функции нескольких переменных является выполнения условия равенства нулю частных производных функции по искомым переменным. Для нашего случая система уравнений имеет вид 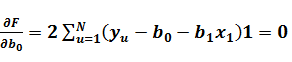 (1.5) (1.5)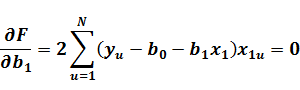 Коэффициенты b0 и b1 рассчитываются по следующим формулам: 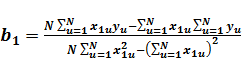 (1.6) (1.6)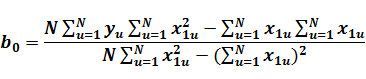 В системе MATHCAD коэффициенты b0 и b1 можно рассчитать следующим образом: b0:=intercept(x, y ) b1:=slope(x, y) (1.7) Для оценки тесноты связи линейной зависимости используется выборочный коэффициент парной корреляции ryx1 , рассчитываемый по формуле: 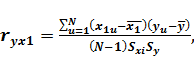 (1.8) (1.8)где N - число экспериментов; - средние значения фактора и выходного параметра; Sx1,Sy - средние квадратичные отклонения x1 и y. 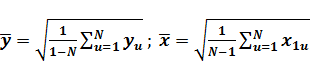 (1.9) (1.9)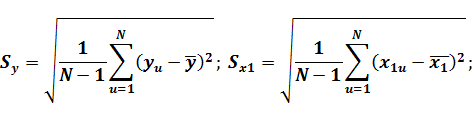 Коэффициент корреляции изменяется от -1 до +1. Чем ближе он к 1, тем сильнее связь между двумя величинами. Знак "+" означает, что обе переменные одновременно возрастают или убывают. Знак "-" наоборот. [4] 5 Достоинства и недостатки метода При пассивном обследовании исследователь не вмешивается в технологический процесс. Анализируется работа объекта при нормальном технологическом режиме. Состояние процесса регулярно фиксируется аппаратчиками и лаборантами в сменных журналах. Регистрация параметров может проводиться группой исследователей непосредственно со щитов управления; одновременно отбираются пробы на анализ. Обязательное условие пассивного эксперимента – одновременная запись значений переменных и отбор проб на анализ через определенные промежутки времени. При пассивном наблюдении используются методы математической статистики для обработки информации с целью изучения закономерностей технологического или экономического процесса. Для обработки результатов пассивного наблюдения чаще всего используют дисперсионный, корреляционный и регрессионный анализы. Пассивный эксперимент имеет следующие недостатки: – диапазон изменений факторов незначителен и не превышает значений, ограничиваемых технологической инструкцией; – влияние возмущающих параметров может оказаться более существенным, чем изменение контролируемых факторов. Указанные недостатки снижают надежность результатов. Но, несмотря на эти недостатки, пассивный эксперимент широко применяется для глубокого анализа результатов работы металлургических процессов и аппаратов. Учитывая, что результаты пассивного эксперимента получаются попутно, без особых затрат, полученной информацией не следует пренебрегать. Следует только не забывать возможность некоторого искажения оценок. Список использованных источников 1. Самойлов Н.А., Учебное пособие по дисциплине «Моделирование в химической технологии расчет реакторов»: Учебное пособие. – Уфа: Изд-во ССП УГНТУ «ИДПО», 2016 - 157 с.; 2. http://mido.kiev.ua/kpi/pe/slavutsky/ind.html; 3. http://mm.lti-gti.ru/works_lectures/SAXT/8.htm – Формальные методы построения математических моделей; 4. http://main.isuct.ru/files/publ/PUBL_ALL/mahp/mahp_19012009.pdf Моделирование и расчет химических процессов; 5. Закгейм А.Ю. Введение в моделирование химико-технологических процессов. – М.: Химия. – 1982. – 223 с. 6. http://www.e-ng.ru/ximiya/metod_modelirovaniya_v_ximii.html Метод моделирования в химии. 7. https://studopedia.ru/2_16972_staticheskie-i-dinamicheskie-modeli.html Статические и динамические модели; |
