выч метод лаба1. лаба1 выч мет. Институт инженерных и цифровых технологий кафедра математического и программного обеспечения информационных систем

• Название: Институт инженерных и цифровых технологий кафедра математического и программного обеспечения информационных систем
• Анкор: выч метод лаба1
• Дата: 22.12.2022
• Размер: 154.33 Kb.
• Имя файла: лаба1 выч мет.docx
• Тип: Отчет; #859109

1йФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»

(НИУ «БелГУ»)

ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ

КАФЕДРА МАТЕМАТИЧЕСКОГО И ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ИНФОРМАЦИОННЫХ СИСТЕМ

Вычислительные методы

Отчет по лабораторной работе № 1

Студента 3 курса группы 12002003

Кулинич Даниил Сергеевич

Проверила:

Бурданова Екатерина Васильевна

_____________________________

Белгород 2022

Тема: «Приближенные значения величин»

Задание: Дано целое неотрицательное число k. Вычислить приближенное значение интегралов от I0 до I30, и от I30 до I0, где Ik=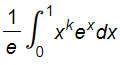

Ход Работы

1. 
   Необходимые начальные I0 и I30 для нахождения приближенных величин интеграла в диапазоне от 0 к 30:
   

I0 = 0.63212055882855767840447622983854

I30 = 0.0312796739321681

2. 
   Формулы необходимые для вычисления значений диапазона от 0 к 30 и от 30 к 0:
   

От 0 к 30:



От 30 к 0: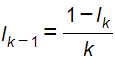



Блок-схема алгоритма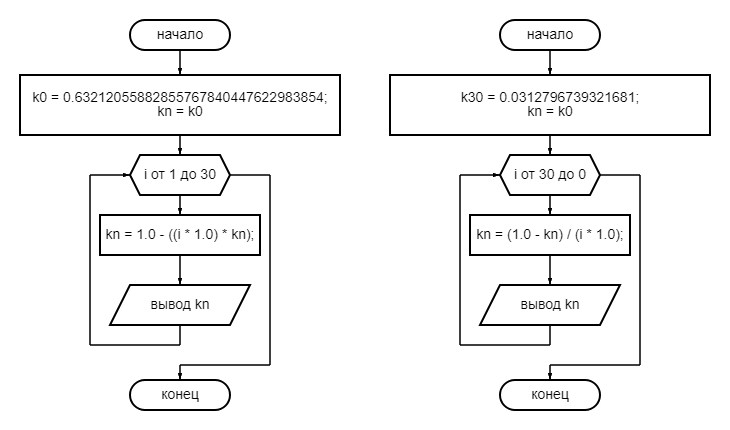



Листинг программы на C#

Основной алгоритм:

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;
namespace лаба1

{

public partial class Form1 : Form

{

public Form1()

{

InitializeComponent();

}
private void button1_Click(object sender, EventArgs e)

{

double k0 = 0.63212055882855767840447622983854;

double kn = 0.63212055882855767840447622983854;

textBox1.Text += 1 + ")" + k0 + "\n\n";

for (int i = 1; i < 30; i++)

{

kn = 1.0 - ((i * 1.0) * kn);

textBox1.Text += i + 1 + ")" + kn + "\r\n\n";

}
}
private void button2_Click(object sender, EventArgs e)

{

double k30 = 0.0312796739321681;

double kn = 0.0312796739321681;

textBox2.Text += 30 + ")" + k30 + "\n\n";

for (int i = 30; i > 0; i--)

{

kn = (1.0 - kn) / (i * 1.0);

textBox2.Text += i - 1 + ")" + kn + "\r\n\n";

}
}

}

}

Тестирование

Запуск программы:



Программа вывела значения по умолчанию и запросила у пользователя запустить алгоритм для вычисления приближенного значения уравнения.

Запуск алгоритма от 0 до 30: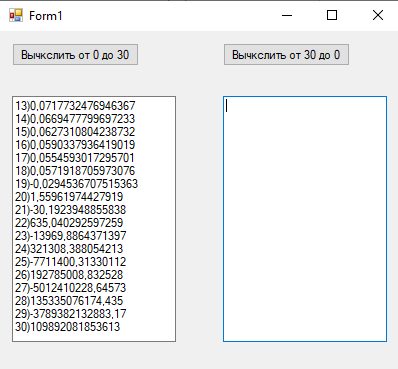



Запуск алгоритма от 30 до 0: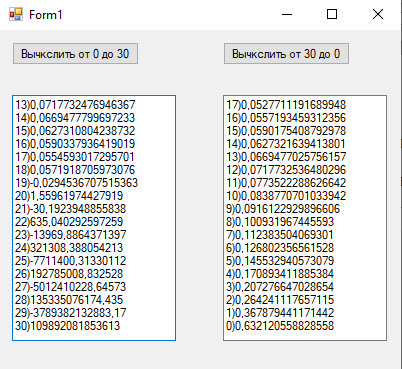



Программа выдала пользователю вычисленные значения.

Проверка значений I0 найденных двумя способами: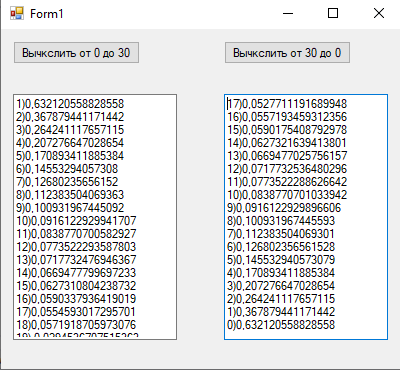



Значения от I0, вплоть до I4, идентичны, дальше идет небольшая погрешность.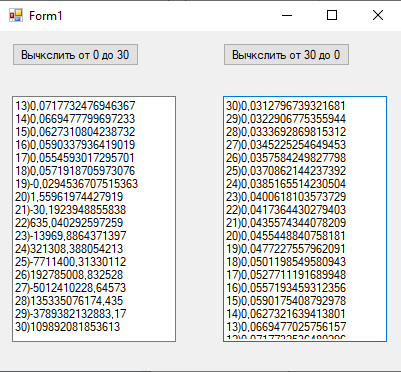



Значения при нахождении от 0 к 30 начиная после I18 начинают расходиться.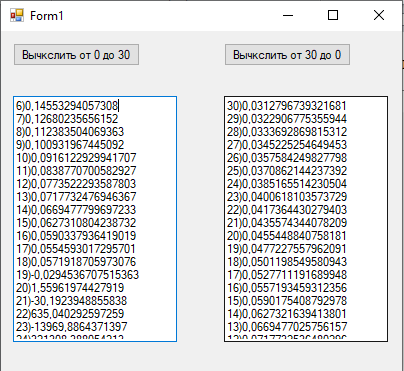



Исходя из результатов теста видно, что при движении от I0 к I30, результаты начинают расходится из-за погрешности, но при движении от I30 к I0, такого не происходит, а значит, что результаты сходятся.

Вывод:

В ходе данной лабораторной работы было произведено приближенное вычисление величин. Выяснено, что при нахождении значений от 0 к 30, значения начинают расходиться начиная после I18, но при движении от 30 к 0 значения наоборот сходятся, а это значит, что мы смогли получить приближенное значение величины во втором случае с более высокой точностью.